1. Introduction

1.介绍

In this tutorial, we’ll explain how the in-place sorting algorithm works.

在本教程中，我们将解释原地排序算法如何工作。

2. In-Place Algorithms

2.就地算法

The in-place algorithms are those that don’t need any auxiliary data structure in order to transform the input data. Basically, it means that the algorithm doesn’t use extra space for input manipulation. It practically overrides the input with the output.

就地算法是那些不需要任何辅助数据结构来转换输入数据的算法。基本上，这意味着该算法不使用额外的空间来进行输入操作。它实际上是用输出覆盖了输入。

However, in reality, the algorithm actually may require a small and non-constant additional space for auxiliary variables. The complexity of this space is in most cases O(log n), although sometimes anything less than linear is allowed.

然而，在现实中，该算法实际上可能需要一个小的、非恒定的辅助变量的额外空间。这个空间的复杂性在大多数情况下是O(log n)，尽管有时允许小于线性的东西。

3. Pseudocode

3.伪代码

Let’s now see some pseudocode and compare the in-place algorithm with the out-of-place one.

现在让我们看看一些伪代码，并比较原位算法和非原位算法。

We’ll assume that we want to reverse an array of n numbers.

我们将假设我们要反转一个n数字的数组。

3.1. In-Place Algorithm

3.1.在位算法

If we think about the problem, we’ll see that we have an input array and reversed array as the output. In the end, we don’t actually need our original array, only the reversed one.

如果我们思考一下这个问题，我们会发现我们有一个输入数组和反转数组作为输出。最后，我们实际上不需要我们的原始数组，只需要反转数组。

Then, why wouldn’t we overwrite the input instead of moving its values to the completely new array, as it might look like a most obvious method? To do that, we’ll only need one additional variable to temporarily store the values that we’re currently working with:

那么，为什么我们不重写输入，而要把它的值移到全新的数组中，因为这可能是一个最明显的方法？要做到这一点，我们只需要一个额外的变量来临时存储我们目前正在处理的值。

reversInPlace(array A[n])
    for i from 0 to n/2
    temp = A[i]
    A[i] = A[n - 1 - i]
    A[n - 1 - i] = temp

It’s noteworthy to mention that no matter how big the array is, the extra space that we need will always be O(1) in this case.

值得一提的是，无论阵列有多大，在这种情况下，我们需要的额外空间总是O(1)。

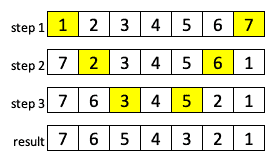
The illustration shows that we need fewer steps than in the previous case:

插图显示，我们需要的步骤比前面的情况少。

3.2. Out-of-Place Algorithm

3.2.离位算法

On the other hand, we can also do this in a pretty simple, more obvious manner. We can create a new array of the same size, copy the values from the original one in the corresponding order and then delete the original array:

另一方面，我们也可以用一种相当简单、更明显的方式来做这件事。我们可以创建一个同样大小的新数组，按照相应的顺序复制原数组中的值，然后删除原数组。

reverseOutOfPlace(array A[n])
    create new array B[n]
    for i from 0 to n - 1
        B[i] = A[i]
    delete A
    return B

Although this will do what we wanted it to do, it’s not efficient enough. We have O(n) extra space required since we have two arrays to manipulate with. Besides that, creating and removing a new array is usually a slow operation.

尽管这将完成我们想要做的事情，但它的效率还不够高。我们有O(n)额外的空间需求 因为我们有两个数组需要操作。除此之外，创建和删除一个新数组通常是一个缓慢的操作。

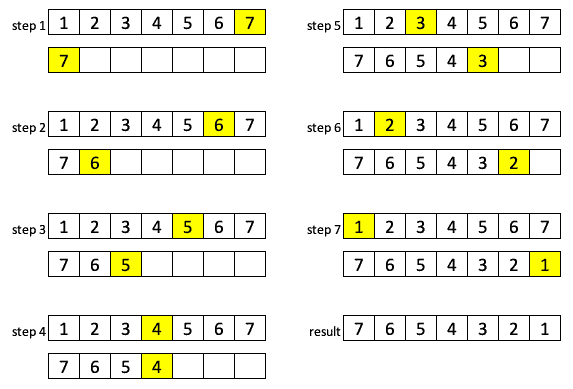
Let’s see the illustration of the process:

让我们看看这个过程的图解。

4. Java Implementation

4.Java实现

Let’s now see how we can implement in Java what we learned in the previous section.

现在让我们看看如何在Java中实现我们在上一节学到的东西。

Firstly, we’ll implement an in-place algorithm:

首先，我们要实现一个就地取材的算法。

public static int[] reverseInPlace(int A[]) {
    int n = A.length;
    for (int i = 0; i < n / 2; i++) {
        int temp = A[i];
        A[i] = A[n - 1 - i];
        A[n - 1 - i] = temp;
    }
    return A;
}

We can test easily that this works as expected:

我们可以很容易地测试这是否如预期的那样工作。

@Test
public void givenArray_whenInPlaceSort_thenReversed() {
    int[] input = {1, 2, 3, 4, 5, 6, 7};
    int[] expected = {7, 6, 5, 4, 3, 2, 1};
    assertArrayEquals("the two arrays are not equal", expected,
      InOutSort.reverseInPlace(input));
}

Secondly, let’s check out the out-of-place algorithm implementation:

其次，我们来看看离位算法的实现。

public static int[] reverseOutOfPlace(int A[]) {
    int n = A.length;
    int[] B = new int[n];
    for (int i = 0; i < n; i++) {
        B[n - i - 1] = A[i];
    }
    return B;
}

The test is pretty straightforward:

该测试是非常直接的。

@Test
public void givenArray_whenOutOfPlaceSort_thenReversed() {
    int[] input = {1, 2, 3, 4, 5, 6, 7};
    int[] expected = {7, 6, 5, 4, 3, 2, 1};
    assertArrayEquals("the two arrays are not equal", expected,
      InOutSort.reverseOutOfPlace(input));
}

5. Examples

5.实例

There are many sorting algorithms that are using in-place approach. Some of them are insertion sort, bubble sort, heap sort, quicksort, and shell sort and you can learn more about them and check-out their Java implementations.

有很多排序算法都是采用就地取材的方式。其中一些是插入排序、气泡排序、堆排序、quicksort和shell排序，你可以进一步了解它们并查看其Java实施。

Also, we need to mention comb sort and heapsort. All these have space complexity O(log n).

此外，我们还需要提到梳理排序和堆叠排序。所有这些都有空间复杂度O（log n）。

It could be also useful to learn more about the Theory of Big-O Notation, as well as to check out some Practical Java Examples about the complexity of the algorithm.

了解更多关于Big-O Notation的理论，以及查看一些关于算法复杂性的实用Java实例，可能也是有用的。

6. Conclusion

6.结论

In this article, we described the so-called in-place algorithms, illustrated how they work using pseudocode and a few examples, listed several algorithms that work on this principle, and finally implemented the basic examples in Java.

在这篇文章中，我们描述了所谓的就地取材算法，用伪代码和一些例子说明了它们是如何工作的，列出了根据这一原则工作的几种算法，最后用Java实现了基本的例子。

As usual, the entire code could be found over on GitHub.

像往常一样，整个代码可以在GitHub上找到超过。