1. Introduction
1.介绍
Pathfinding algorithms are techniques for navigating maps, allowing us to find a route between two different points. Different algorithms have different pros and cons, often in terms of the efficiency of the algorithm and the efficiency of the route that it generates.
寻路算法是导航地图的技术,使我们能够在两个不同的点之间找到一条路线。不同的算法有不同的优点和缺点,通常是在算法的效率和它所产生的路线的效率方面。
2. What Is a Pathfinding Algorithm?
2.什么是寻路算法?
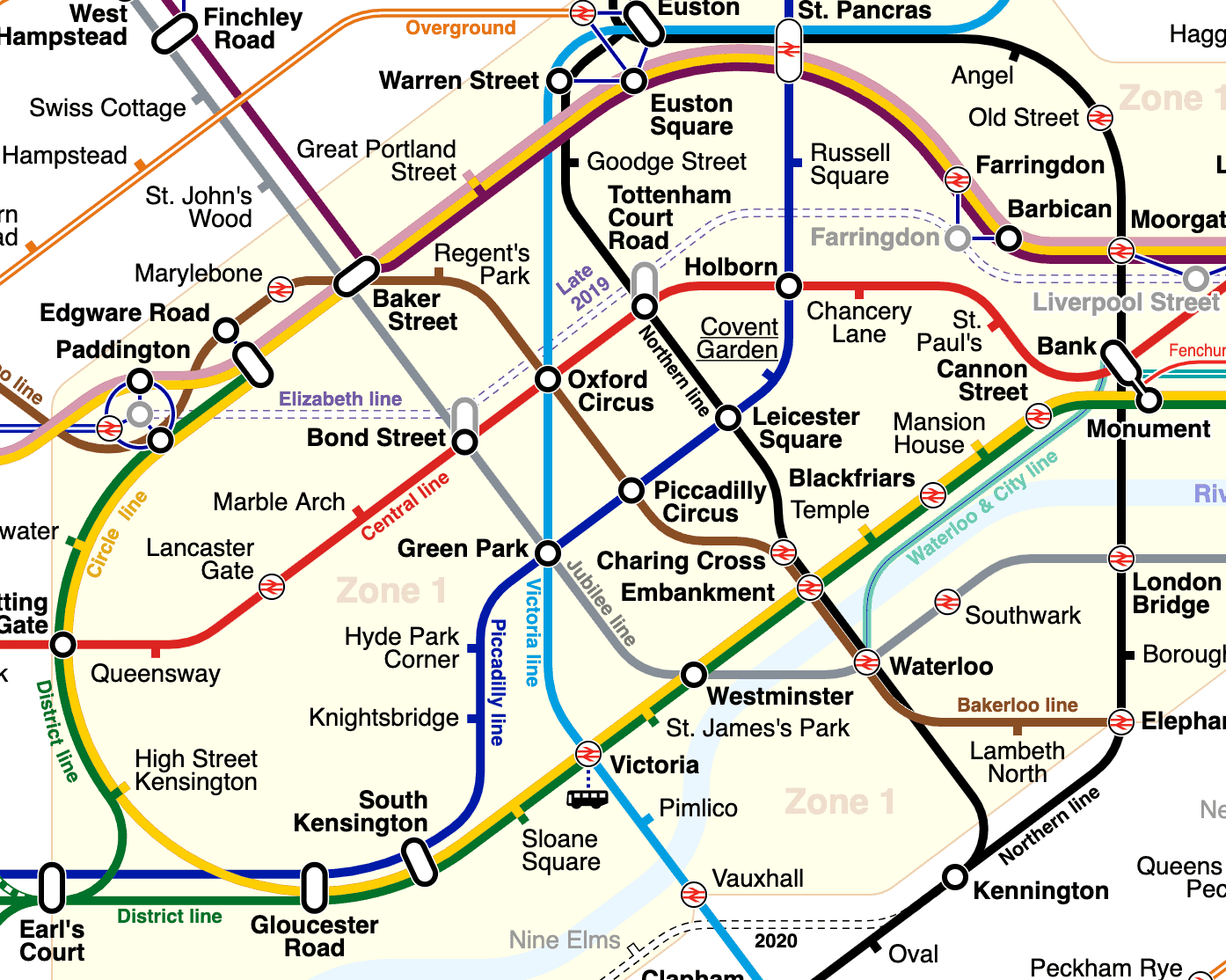
A Pathfinding Algorithm is a technique for converting a graph – consisting of nodes and edges – into a route through the graph. This graph can be anything at all that needs traversing. For this article, we’re going to attempt to traverse a portion of the London Underground system:
寻路算法是一种将图–由节点和边组成–转换为穿越该图的路线的技术。这个图可以是任何需要穿越的东西。在这篇文章中,我们将尝试穿越伦敦地铁系统的一部分。
(“London Underground Overground DLR Crossrail map” by sameboat is licensed under CC BY-SA 4.0)
(“London Underground Overground DLR Crossrail map” by sameboat is licensed under CC BY-SA 4.0)
This has a lot of interesting components to it:
这里面有很多有趣的成分。
- We may or may not have a direct route between our starting and ending points. For example, we can go directly from “Earl’s Court” to “Monument”, but not to “Angel”.
- Every single step has a particular cost. In our case, this is the distance between stations.
- Each stop is only connected to a small subset of the other stops. For example, “Regent’s Park” is directly connected to only “Baker Street” and “Oxford Circus”.
All pathfinding algorithms take as input a collection of all the nodes – stations in our case – and connections between them, and also the desired starting and ending points. The output is typically the set of nodes that will get us from start to end, in the order that we need to go.
所有的寻路算法都把所有的节点–在我们的例子中是车站–和它们之间的连接,以及想要的起点和终点的集合作为输入。输出通常是能让我们按照需要的顺序从起点到终点的节点集合。
3. What Is A*?
3.什么是A*?
A* is one specific pathfinding algorithm, first published in 1968 by Peter Hart, Nils Nilsson, and Bertram Raphael. It is generally considered to be the best algorithm to use when there is no opportunity to pre-compute the routes and there are no constraints on memory usage.
A*是一种特定的寻路算法,由Peter Hart、Nils Nilsson和Bertram Raphael在1968年首次发表。一般认为,当没有机会预先计算路线,并且对内存的使用没有限制时,它是最好的算法。
Both memory and performance complexity can be O(b^d) in the worst case, so while it will always work out the most efficient route, it’s not always the most efficient way to do so.
在最坏的情况下,内存和性能的复杂性都可以达到O(b^d),所以虽然它总是能算出最有效的路线,但它并不总是最有效的方法。
A* is actually a variation on Dijkstra’s Algorithm, where there is additional information provided to help select the next node to use. This additional information does not need to be perfect – if we already have perfect information, then pathfinding is pointless. But the better it is, the better the end result will be.
A*实际上是Dijkstra算法的一个变种,其中提供了额外的信息来帮助选择要使用的下一个节点。这种额外的信息不需要是完美的–如果我们已经有了完美的信息,那么寻路就毫无意义。但它越好,最终的结果就会越好。
4. How Does A* Work?
4.A*是如何工作的?
The A* Algorithm works by iteratively selecting what is the best route so far, and attempting to see what the best next step is.
A*算法的工作方式是迭代选择到目前为止的最佳路线,并尝试查看下一步的最佳路线。。
When working with this algorithm, we have several pieces of data that we need to keep track of. The “open set” is all of the nodes that we are currently considering. This is not every node in the system, but instead, it’s every node that we might make the next step from.
在使用这种算法时,我们有几个数据需要跟踪。”开放集 “是我们目前正在考虑的所有节点。这不是系统中的每一个节点,而是我们可能进行下一步的每个节点。
We’ll also keep track of the current best score, the estimated total score and the current best previous node for each node in the system.
我们还将跟踪系统中每个节点的当前最佳得分、估计总分和当前最佳前一个节点。
As part of this, we need to be able to calculate two different scores. One is the score to get from one node to the next. The second is a heuristic to give an estimate of the cost from any node to the destination. This estimate does not need to be accurate, but greater accuracy is going to yield better results. The only requirement is that both scores are consistent with each other – that is, they’re in the same units.
作为其中的一部分,我们需要能够计算两个不同的分数。一个是从一个节点到下一个节点的分数。第二个是启发式的,对从任何节点到目的地的成本进行估计。这个估计不需要准确,但更大的准确性会产生更好的结果。唯一的要求是这两个分数要相互一致–也就是说,它们的单位是一样的。
At the very start, our open set consists of our start node, and we have no information about any other nodes at all.
在一开始,我们的开放集包括我们的起始节点,而我们根本没有任何其他节点的信息。
At each iteration, we will:
在每个迭代中,我们将。
- Select the node from our open set that has the lowest estimated total score
- Remove this node from the open set
- Add to the open set all of the nodes that we can reach from it
When we do this, we also work out the new score from this node to each new one to see if it’s an improvement on what we’ve got so far, and if it is, then we update what we know about that node.
当我们这样做时,我们也会计算出从这个节点到每个新节点的新分数,看看它是否比我们目前得到的分数有所提高,如果是,那么我们就会更新我们对该节点的了解。。
This then repeats until the node in our open set that has the lowest estimated total score is our destination, at which point we’ve got our route.
然后重复这个过程,直到我们的开放集中估计总分最低的节点是我们的目的地,这时我们就得到了我们的路线。
4.1. Worked Example
4.1.工作实例
For example, let’s start from “Marylebone” and attempt to find our way to “Bond Street”.
例如,让我们从 “Marylebone “开始,试图找到前往 “Bond Street “的路。
At the very start, our open set consists only of “Marylebone”. That means that this is implicitly the node that we’ve got the best “estimated total score” for.
在一开始,我们的开放集只包括 “Marylebone”。这意味着这是我们得到最佳 “估计总分 “的隐含节点。
Our next stops can be either “Edgware Road”, with a cost of 0.4403 km, or “Baker Street”, with a cost of 0.4153 km. However, “Edgware Road” is in the wrong direction, so our heuristic from here to the destination gives a score of 1.4284 km, whereas “Baker Street” has a heuristic score of 1.0753 km.
我们的下一站可以是 “埃奇韦尔路”,费用为0.4403公里,也可以是 “贝克街”,费用为0.4153公里。然而,”埃奇韦尔路 “的方向是错误的,所以我们从这里到目的地的启发式得分是1.4284公里,而 “贝克街 “的启发式得分是1.0753公里。
This means that after this iteration our open set consists of two entries – “Edgware Road”, with an estimated total score of 1.8687 km, and “Baker Street”, with an estimated total score of 1.4906 km.
这意味着在这次迭代之后,我们的开放集包括两个条目–“埃奇韦尔路”,估计总分是1.8687公里,以及 “贝克街”,估计总分是1.4906公里。
Our second iteration will then start from “Baker Street”, since this has the lowest estimated total score. From here, our next stops can be either “Marylebone”, “St. John’s Wood”, “Great Portland Street”, Regent’s Park”, or “Bond Street”.
我们的第二次迭代将从 “贝克街 “开始,因为它的估计总分最低。从这里开始,我们的下一站可以是 “玛丽伯恩”、”圣约翰森林”、”大波特兰街”、摄政公园,或者 “邦德街”。
We won’t work through all of these, but let’s take “Marylebone” as an interesting example. The cost to get there is again 0.4153 km, but this means that the total cost is now 0.8306 km. Additionally the heuristic from here to the destination gives a score of 1.323 km.
我们不会对所有这些进行研究,但让我们把 “Marylebone “作为一个有趣的例子。到达那里的成本又是0.4153公里,但这意味着现在的总成本是0.8306公里。此外,从这里到目的地的启发式方法给出的分数是1.323公里。
This means that the estimated total score would be 2.1536 km, which is worse than the previous score for this node. This makes sense because we’ve had to do extra work to get nowhere in this case. This means that we will not consider this a viable route. As such, the details for “Marylebone” are not updated, and it is not added back onto the open set.
这意味着估计的总分将是2.1536公里,比之前这个节点的得分要差。这是有道理的,因为在这种情况下,我们不得不做额外的工作,以达到无处不在的效果。这意味着我们将不认为这是一条可行的路线。因此,”Marylebone “的详细信息不会被更新,也不会被重新添加到开放集上。
5. Java Implementation
5.Java实现
Now that we’ve discussed how this works, let’s actually implement it. We’re going to build a generic solution, and then we’ll implement the code necessary for it to work for the London Underground. We can then use it for other scenarios by implementing only those specific parts.
现在我们已经讨论了这一工作方式,让我们来实际实现它。我们将建立一个通用的解决方案,然后我们将实现它在伦敦地铁上运行所需的代码。然后我们可以通过只实现那些特定的部分将它用于其他场景。
5.1. Representing the Graph
5.1.图形的表示
Firstly, we need to be able to represent our graph that we wish to traverse. This consists of two classes – the individual nodes and then the graph as a whole.
首先,我们需要能够表示我们希望穿越的图。这包括两类–单个节点,然后是整个图。
We’ll represent our individual nodes with an interface called GraphNode:
我们将用一个叫做GraphNode的接口来表示我们的各个节点。
public interface GraphNode {
String getId();
}Each of our nodes must have an ID. Anything else is specific to this particular graph and is not needed for the general solution. These classes are simple Java Beans with no special logic.
我们的每个节点都必须有一个ID。其他的都是针对这个特定图形的,对于一般的解决方案来说是不需要的。这些类是简单的Java Bean,没有特殊的逻辑。
Our overall graph is then represented by a class simply called Graph:
我们的整体图形就由一个简单的叫做Graph的类来表示。
public class Graph<T extends GraphNode> {
private final Set<T> nodes;
private final Map<String, Set<String>> connections;
public T getNode(String id) {
return nodes.stream()
.filter(node -> node.getId().equals(id))
.findFirst()
.orElseThrow(() -> new IllegalArgumentException("No node found with ID"));
}
public Set<T> getConnections(T node) {
return connections.get(node.getId()).stream()
.map(this::getNode)
.collect(Collectors.toSet());
}
}This stores all of the nodes in our graph and has knowledge of which nodes connect to which. We can then get any node by ID, or all of the nodes connected to a given node.
它存储了我们图中的所有节点,并且知道哪些节点连接到哪些节点。然后我们可以通过ID获得任何节点,或者获得连接到某个节点的所有节点。
At this point, we’re capable of representing any form of graph we wish, with any number of edges between any number of nodes.
在这一点上,我们能够代表我们希望的任何形式的图,任何数量的节点之间有任何数量的边。
5.2. Steps on Our Route
5.2.我们路线上的步骤
The next thing we need is our mechanism for finding routes through the graph.
接下来我们需要的是我们在图中寻找路线的机制。
The first part of this is some way to generate a score between any two nodes. We’ll the Scorer interface for both the score to the next node and the estimate to the destination:
第一部分是在任何两个节点之间生成分数的某种方式。我们将通过Scorer接口来获得对下一个节点的分数和对目的地的估计。
public interface Scorer<T extends GraphNode> {
double computeCost(T from, T to);
}Given a start and an end node, we then get a score for traveling between them.
给出一个起点和一个终点节点,我们就可以得到在它们之间旅行的分数。
We also need a wrapper around our nodes that carries some extra information. Instead of being a GraphNode, this is a RouteNode – because it’s a node in our computed route instead of one in the entire graph:
我们还需要一个围绕我们的节点的包装器,携带一些额外的信息。这不是一个GraphNode,而是一个RouteNode–因为它是我们计算路线中的一个节点,而不是整个图中的一个。
class RouteNode<T extends GraphNode> implements Comparable<RouteNode> {
private final T current;
private T previous;
private double routeScore;
private double estimatedScore;
RouteNode(T current) {
this(current, null, Double.POSITIVE_INFINITY, Double.POSITIVE_INFINITY);
}
RouteNode(T current, T previous, double routeScore, double estimatedScore) {
this.current = current;
this.previous = previous;
this.routeScore = routeScore;
this.estimatedScore = estimatedScore;
}
}As with GraphNode, these are simple Java Beans used to store the current state of each node for the current route computation. We’ve given this a simple constructor for the common case, when we’re first visiting a node and have no additional information about it yet.
与GraphNode一样,这些都是简单的Java Bean,用于存储当前路由计算中每个节点的当前状态。我们已经为常见的情况给出了一个简单的构造函数,当我们第一次访问一个节点时,还没有关于它的额外信息。
These also need to be Comparable though, so that we can order them by the estimated score as part of the algorithm. This means the addition of a compareTo() method to fulfill the requirements of the Comparable interface:
但这些也需要Comparable,这样我们就可以作为算法的一部分按照估计的分数来排序。这意味着增加了一个compareTo()方法来满足Comparable接口的要求。
@Override
public int compareTo(RouteNode other) {
if (this.estimatedScore > other.estimatedScore) {
return 1;
} else if (this.estimatedScore < other.estimatedScore) {
return -1;
} else {
return 0;
}
}5.3. Finding Our Route
5.3.寻找我们的路线
Now we’re in a position to actually generate our routes across our graph. This will be a class called RouteFinder:
现在我们可以在我们的图中实际生成我们的路线。这将是一个叫做RouteFinder的类。
public class RouteFinder<T extends GraphNode> {
private final Graph<T> graph;
private final Scorer<T> nextNodeScorer;
private final Scorer<T> targetScorer;
public List<T> findRoute(T from, T to) {
throw new IllegalStateException("No route found");
}
}We have the graph that we are finding the routes across, and our two scorers – one for the exact score for the next node, and one for the estimated score to our destination. We’ve also got a method that will take a start and end node and compute the best route between the two.
我们有寻找路线的图,还有两个评分器–一个是下一个节点的准确分数,一个是到目的地的估计分数。我们也有一个方法,它将接受一个起点和终点节点,并计算出两者之间的最佳路线。
This method is to be our A* algorithm. All the rest of our code goes inside this method.
这个方法将是我们的A*算法。我们所有其他的代码都在这个方法里面。
We start with some basic setup – our “open set” of nodes that we can consider as the next step, and a map of every node that we’ve visited so far and what we know about it:
我们从一些基本设置开始–我们的 “开放集 “节点,我们可以考虑作为下一步,以及我们迄今为止访问过的每个节点的地图和我们对它的了解。
Queue<RouteNode> openSet = new PriorityQueue<>();
Map<T, RouteNode<T>> allNodes = new HashMap<>();
RouteNode<T> start = new RouteNode<>(from, null, 0d, targetScorer.computeCost(from, to));
openSet.add(start);
allNodes.put(from, start);Our open set initially has a single node – our start point. There is no previous node for this, there’s a score of 0 to get there, and we’ve got an estimate of how far it is from our destination.
我们的开放集最初有一个节点–我们的起点。这个节点没有前一个节点,到达那里的分数是0,而且我们已经估算出了它离我们的目的地有多远。
The use of a PriorityQueue for the open set means that we automatically get the best entry off of it, based on our compareTo() method from earlier.
对开放集使用PriorityQueue意味着我们会根据之前的compareTo()方法,自动从其中获取最佳条目。
Now we iterate until either we run out of nodes to look at, or the best available node is our destination:
现在,我们进行迭代,直到我们用完了要看的节点,或者最佳可用节点是我们的目的地。
while (!openSet.isEmpty()) {
RouteNode<T> next = openSet.poll();
if (next.getCurrent().equals(to)) {
List<T> route = new ArrayList<>();
RouteNode<T> current = next;
do {
route.add(0, current.getCurrent());
current = allNodes.get(current.getPrevious());
} while (current != null);
return route;
}
// ...When we’ve found our destination, we can build our route by repeatedly looking at the previous node until we reach our starting point.
当我们找到目的地后,我们可以通过重复查看前一个节点来建立我们的路线,直到我们到达我们的起点。
Next, if we haven’t reached our destination, we can work out what to do next:
接下来,如果我们还没有到达目的地,我们可以想出下一步该怎么做:。
graph.getConnections(next.getCurrent()).forEach(connection -> {
RouteNode<T> nextNode = allNodes.getOrDefault(connection, new RouteNode<>(connection));
allNodes.put(connection, nextNode);
double newScore = next.getRouteScore() + nextNodeScorer.computeCost(next.getCurrent(), connection);
if (newScore < nextNode.getRouteScore()) {
nextNode.setPrevious(next.getCurrent());
nextNode.setRouteScore(newScore);
nextNode.setEstimatedScore(newScore + targetScorer.computeCost(connection, to));
openSet.add(nextNode);
}
});
throw new IllegalStateException("No route found");
}Here, we’re iterating over the connected nodes from our graph. For each of these, we get the RouteNode that we have for it – creating a new one if needed.
这里,我们正在迭代我们图中的连接节点。对于每一个节点,我们都会得到我们拥有的RouteNode–如果需要的话,创建一个新的节点。
We then compute the new score for this node and see if it’s cheaper than what we had so far. If it is then we update it to match this new route and add it to the open set for consideration next time around.
然后我们计算这个节点的新分数,看看它是否比我们到目前为止的分数更便宜。如果是的话,我们就更新它,使之与这条新路线相匹配,并将其加入开放集,供下次考虑。
This is the entire algorithm. We keep repeating this until we either reach our goal or fail to get there.
这就是整个算法。我们不断重复这一点,直到我们达到目标或未能达到目标。
5.4. Specific Details for the London Underground
5.4.伦敦地铁的具体细节
What we have so far is a generic A* pathfinder, but it’s lacking the specifics we need for our exact use case. This means we need a concrete implementation of both GraphNode and Scorer.
到目前为止,我们所拥有的是一个通用的A*寻路者,但它缺乏我们在具体使用案例中所需要的细节。这意味着我们需要一个GraphNode和Scorer的具体实现。
Our nodes are stations on the underground, and we’ll model them with the Station class:
我们的节点是地下的车站,我们将用Station类为它们建模。
public class Station implements GraphNode {
private final String id;
private final String name;
private final double latitude;
private final double longitude;
}The name is useful for seeing the output, and the latitude and longitude are for our scoring.
名称对于查看输出结果很有用,而经纬度是为了我们的评分。
In this scenario, we only need a single implementation of Scorer. We’re going to use the Haversine formula for this, to compute the straight-line distance between two pairs of latitude/longitude:
在这种情况下,我们只需要一个Scorer的实现。我们将为此使用Haversine公式,以计算两对纬度/经度之间的直线距离。
public class HaversineScorer implements Scorer<Station> {
@Override
public double computeCost(Station from, Station to) {
double R = 6372.8; // Earth's Radius, in kilometers
double dLat = Math.toRadians(to.getLatitude() - from.getLatitude());
double dLon = Math.toRadians(to.getLongitude() - from.getLongitude());
double lat1 = Math.toRadians(from.getLatitude());
double lat2 = Math.toRadians(to.getLatitude());
double a = Math.pow(Math.sin(dLat / 2),2)
+ Math.pow(Math.sin(dLon / 2),2) * Math.cos(lat1) * Math.cos(lat2);
double c = 2 * Math.asin(Math.sqrt(a));
return R * c;
}
}We now have almost everything necessary to calculate paths between any two pairs of stations. The only thing missing is the graph of connections between them.
我们现在几乎拥有计算任何两对车站之间的路径所需的一切。唯一缺少的是它们之间的连接图。
Let’s use it for mapping out a route. We’ll generate one from Earl’s Court up to Angel. This has a number of different options for travel, on a minimum of two tube lines:
让我们用它来绘制一条路线。我们将生成一条从伯爵府到天使的路线。这有许多不同的出行选择,至少有两条地铁线路。
public void findRoute() {
List<Station> route = routeFinder.findRoute(underground.getNode("74"), underground.getNode("7"));
System.out.println(route.stream().map(Station::getName).collect(Collectors.toList()));
}This generates a route of Earl’s Court -> South Kensington -> Green Park -> Euston -> Angel.
这产生了一条伯爵府->;南肯辛顿->;绿色公园->;尤斯顿->;天使的路线。。
The obvious route that many people would have taken would likely be Earl’s Count -> Monument -> Angel, because that’s got fewer changes. Instead, this has taken a significantly more direct route even though it meant more changes.
许多人可能会采取的明显路线是伯爵府->纪念碑->天使,因为这样的变化较少。相反,这是一条明显更直接的路线,尽管它意味着更多的变化。
6. Conclusion
6.结论
In this article, we’ve seen what the A* algorithm is, how it works, and how to implement it in our own projects. Why not take this and extend it for your own uses?
在这篇文章中,我们已经看到了什么是A*算法,它是如何工作的,以及如何在我们自己的项目中实现它。为什么不以此为基础,为你自己的用途进行扩展呢?
Maybe try to extend it to take interchanges between tube lines into account, and see how that affects the selected routes?
也许可以尝试扩展它,将地铁线路之间的交汇点考虑在内,看看这对所选线路有什么影响?
And again, the complete code for the article is available over on GitHub.
再说一遍,该文章的完整代码可在GitHub上找到,。