Prim’s Algorithm with a Java Implementation – 普利姆算法的Java实现

1. Introduction

1.绪论

In this tutorial, we first learn what minimum spanning trees are. Afterward, we’ll use Prim’s algorithm to find one.

在本教程中，我们首先学习什么是最小生成树。之后，我们将使用Prim的算法来寻找一个。

2. Minimum Spanning Tree

2.最小生成树

A minimum spanning tree (MST) is a weighted, undirected, connected graph whose total edge weight has been minimized by removing heavier edges. In other words, we keep all the vertices of the graph intact, but we may remove some edges so that the sum of all edges is at a minimum.

最小生成树（MST）是一个加权的、无定向的、连接的图，其总的边重已经通过移除较重的边而达到最小化。换句话说，我们保持图形的所有顶点不变，但我们可以删除一些边，使所有边的总和达到最小。

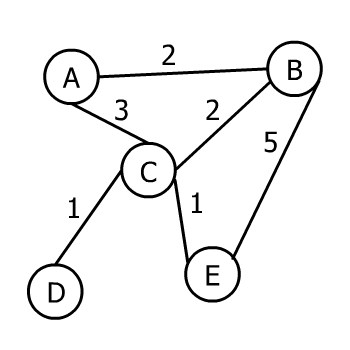
We start with a weighted graph since it makes no sense to minimize the total edge weight if those edges have no weight at all. Let’s take a look at an example graph:

我们从一个加权图开始，因为如果这些边根本没有权重，那么最小化总边的权重就没有意义。让我们看一下一个例子图。

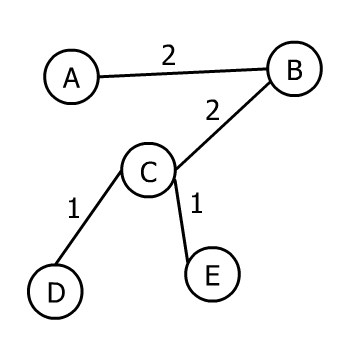
The above graph is a weighted, undirected, connected graph. Here is an MST of that graph:

上面的图是一个加权的、无定向的、连接的图。下面是该图的MST。

An MST of a graph is not unique, though. If a graph has more than one MST, then each MST has the same total edge weight.

不过，一个图的MST不是唯一的。如果一个图有一个以上的MST，那么每个MST都有相同的总边重。

3. Prim’s Algorithm

3.普利姆的算法

Prim’s algorithm takes a weighted, undirected, connected graph as input and returns an MST of that graph as output.

Prim的算法将一个加权、无定向、连接的图作为输入，并返回该图的MST作为输出。

It works in a greedy manner. In the first step, it selects an arbitrary vertex. Thereafter, each new step adds the nearest vertex to the tree constructed so far until there is no disconnected vertex left.

它以一种贪婪的方式工作。在第一步，它选择了一个任意的顶点。此后，每一个新的步骤都将最近的顶点添加到迄今为止构建的树上，直到没有断开的顶点。

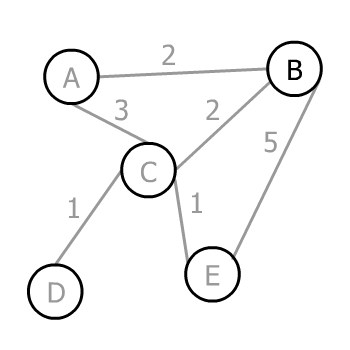
Let’s run Prim’s algorithm on this graph step-by-step:

让我们在这个图上一步步运行Prim的算法。

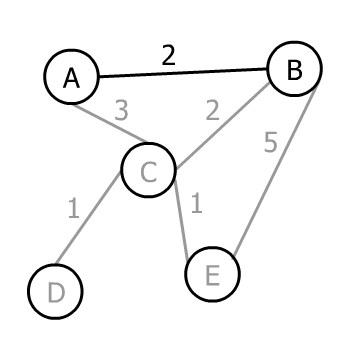
Assuming the arbitrary vertex to start the algorithm is B, we have three choices A, C, and E to go. The corresponding weights of the edges are 2, 2, and 5, therefore the minimum is 2. In this case, we have two edges weighing 2, so we can choose either of them (it doesn’t matter which one). Let’s choose A:

假设开始算法的任意顶点是B，我们有三个选择A、C和E去。在这种情况下，我们有两条重量为2的边，所以我们可以选择其中任何一条（哪一条并不重要）。让我们选择A。

Now we have a tree with two vertices A and B. We can select any of A or B’s edges not yet added that lead to an unadded vertex. So, we can pick AC, BC, or BE.

现在我们有一棵有两个顶点A和B的树，我们可以选择A或B的任何一条尚未添加的、通向未添加顶点的边。因此，我们可以选择AC、BC或BE。

Prim’s algorithm chooses the minimum, which is 2, or BC:

Prim的算法选择最小值，即2，或BC。

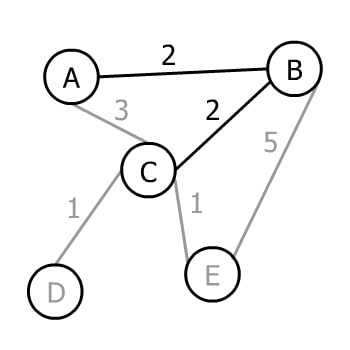
Now we have a tree with three vertices and three possible edges to move forward: CD, CE, or BE. AC isn’t included since it wouldn’t add a new vertex to the tree. The minimum weight amongst these three is 1.

现在我们有一棵有三个顶点的树，有三条可能的边可以向前移动。CD，CE，或BE。AC不包括在内，因为它不会给树增加一个新的顶点。这三条边的最小权重是1。

However, there are two edges both weighing 1. Consequently, Prim’s algorithm chooses one of them (again doesn’t matter which one) in this step: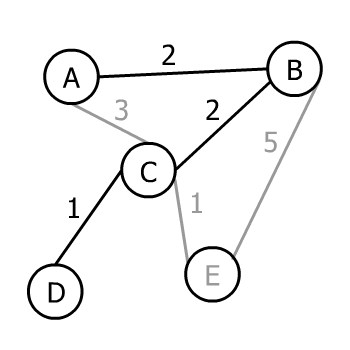

然而，有两条边的权重都是1。因此，Prim的算法在这一步选择了其中一条（同样也不管是哪一条）：

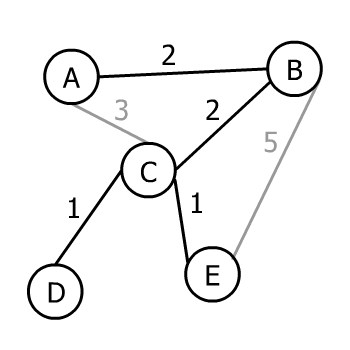
There is only one vertex left to join, so we can pick from CE and BE. The minimum weight that can connect our tree to it is 1, and Prim’s algorithm will choose it:

只剩下一个顶点可以连接，所以我们可以从CE和BE中挑选。能把我们的树连接到它的最小权重是1，Prim的算法会选择它。

As all vertices of the input graph are now present in the output tree, Prim’s algorithm ends. Therefore, this tree is an MST of the input graph.

由于输入图的所有顶点现在都出现在输出树中，Prim的算法结束了。因此，这棵树是输入图的一个MST。

4. Implementation

4.实施

Vertices and edges make graphs, so we need a data structure to store these elements. Let’s create the class Edge:

顶点和边构成图，所以我们需要一个数据结构来存储这些元素。让我们创建一个Edge类。

public class Edge {

    private int weight;
    private boolean isIncluded = false;

}

Each Edge must have a weight since Prim’s algorithm works on weighted graphs. isIncluded shows whether the Edge is present in the minimum spanning tree or not.

每个Edge必须有一个权重，因为Prim的算法在加权图上工作。isIncluded显示Edge是否存在于最小生成树中。

Now, let’s add the Vertex class:

现在，让我们添加Vertex类。

public class Vertex {

    private String label = null;
    private Map<Vertex, Edge> edges = new HashMap<>();
    private boolean isVisited = false;

}

Each Vertex can optionally have a label. We use the edges map to store connections among vertices. Finally, isVisited shows whether the vertex has been visited by Prim’s algorithm so far or not.

每个顶点可以选择有一个标签。我们使用edges映射来存储顶点之间的连接。最后，isVisited显示顶点到目前为止是否被Prim的算法访问过。

Let’s create our Prim class where we’ll implement the logic:

让我们创建我们的Prim类，在那里我们将实现逻辑。

public class Prim {

    private List<Vertex> graph;

}

A list of vertices is enough to store the whole graph because inside each Vertex, we have a Map<Vertex, Edge> to identify all connections. Inside Prim, we create a run() method:

一个顶点列表足以存储整个图形，因为在每个Vertex里面，我们有一个Map<Vertex, Edge>来识别所有的连接。在Prim里面，我们创建了一个run() 方法。

public void run() {
    if (graph.size() > 0) {
        graph.get(0).setVisited(true);
    }
    while (isDisconnected()) {
        Edge nextMinimum = new Edge(Integer.MAX_VALUE);
        Vertex nextVertex = graph.get(0);
        for (Vertex vertex : graph) {
            if (vertex.isVisited()) {
                Pair<Vertex, Edge> candidate = vertex.nextMinimum();
                if (candidate.getValue().getWeight() < nextMinimum.getWeight()) {
                    nextMinimum = candidate.getValue();
                    nextVertex = candidate.getKey();
                }
            }
        }
        nextMinimum.setIncluded(true);
        nextVertex.setVisited(true);
    }
}

We start by setting the first element of the List<Vertex> graph as visited. The first element can be any of the vertices depending on the order they’ve been added to the list in the first place. isDisconnected() returns true if there is any Vertex not visited so far:

我们首先将List<Vertex>graph的第一个元素设置为被访问。第一个元素可以是任何一个顶点，这取决于它们最初被添加到列表中的顺序。isDisconnected()如果有任何顶点至今未被访问，则返回真。

private boolean isDisconnected() {
    for (Vertex vertex : graph) {
        if (!vertex.isVisited()) {
            return true;
        }
    }
    return false;
}

While the minimum spanning tree isDisconnected(), we loop over the already visited vertices and find the Edge with the minimum weight as a candidate for nextVertex:

当最小生成树isDisconnected()时，我们在已经访问过的顶点上循环，找到权重最小的Edge，作为nextVertex的候选者：。

public Pair<Vertex, Edge> nextMinimum() {
    Edge nextMinimum = new Edge(Integer.MAX_VALUE);
    Vertex nextVertex = this;
    Iterator<Map.Entry<Vertex,Edge>> it = edges.entrySet()
        .iterator();
    while (it.hasNext()) {
        Map.Entry<Vertex,Edge> pair = it.next();
        if (!pair.getKey().isVisited()) {
            if (!pair.getValue().isIncluded()) {
                if (pair.getValue().getWeight() < nextMinimum.getWeight()) {
                    nextMinimum = pair.getValue();
                    nextVertex = pair.getKey();
                }
            }
        }
    }
    return new Pair<>(nextVertex, nextMinimum);
}

We find the minimum of all candidates in the main loop and store it in nextVertex.  Then, we set nextVertex as visited. The loop goes on until all vertices are visited.

我们在主循环中找到所有候选s的最小值，并将其存储在nextVertex中。 然后，我们将nextVertex设为已访问。这个循环一直持续到所有顶点都被访问过为止。

At the end, each Edge with isIncluded equal to true is present.

在最后，每个Edge的isIncluded等于true的都存在。

Note that since nextMinimum() iterates through the edges, the time complexity of this implementation is O(V²). If we store the edges in a priority queue (sorted by weight) instead, the algorithm will perform in O(E log V).

请注意，由于nextMinimum()在边上进行迭代，这个实现的时间复杂度为O(V²)。如果我们将边存储在一个优先级队列中（按权重排序），该算法将以O(E log V)执行。

5. Testing

5.测试

Okay, so now that we’ve got some code, let’s test it with a real example. First, we construct our graph:

好了，现在我们已经有了一些代码，让我们用一个真实的例子来测试它。首先，我们构建我们的图。

public static List<Vertex> createGraph() {
    List<Vertex> graph = new ArrayList<>();
    Vertex a = new Vertex("A");
    ...
    Vertex e = new Vertex("E");
    Edge ab = new Edge(2);
    a.addEdge(b, ab);
    b.addEdge(a, ab);
    ...
    Edge ce = new Edge(1);
    c.addEdge(e, ce);
    e.addEdge(c, ce);
    graph.add(a);
    ...
    graph.add(e);
    return graph;
}

The constructor of the Prim class takes it and stores it inside the class. We can print the input graph with originalGraphToString() method:

Prim类的构造函数接收它并将其存储在类内。我们可以用originalGraphToString()方法打印输入图。

Prim prim = new Prim(createGraph());
System.out.println(prim.originalGraphToString());

Our example will output:

我们的例子将输出。

A --- 2 --- B
A --- 3 --- C
B --- 5 --- E
B --- 2 --- C
C --- 1 --- E
C --- 1 --- D

Now, we run Prim’s algorithm and print the resulting MST with minimumSpanningTreeToString() method:

现在，我们运行Prim的算法，用minimumSpanningTreeToString()方法打印出结果的MST。

prim.run();
prim.resetPrintHistory();
System.out.println(prim.minimumSpanningTreeToString());

Finally, we print out our MST:

最后，我们打印出我们的MST。

A --- 2 --- B
B --- 2 --- C
C --- 1 --- E
C --- 1 --- D

6. Conclusion

6.结语

In this article, we learned how Prim’s algorithm finds a minimum spanning tree of a graph. The code is available over on GitHub.

在这篇文章中，我们学习了Prim的算法如何找到图的最小生成树。该代码可在GitHub上获得。