1. Overview
1.概述
In this tutorial, we’ll look at how to implement a min-max heap in Java.
在本教程中,我们将了解如何在Java中实现最小-最大堆。
2. Min-Max Heap
2.最小-最大堆
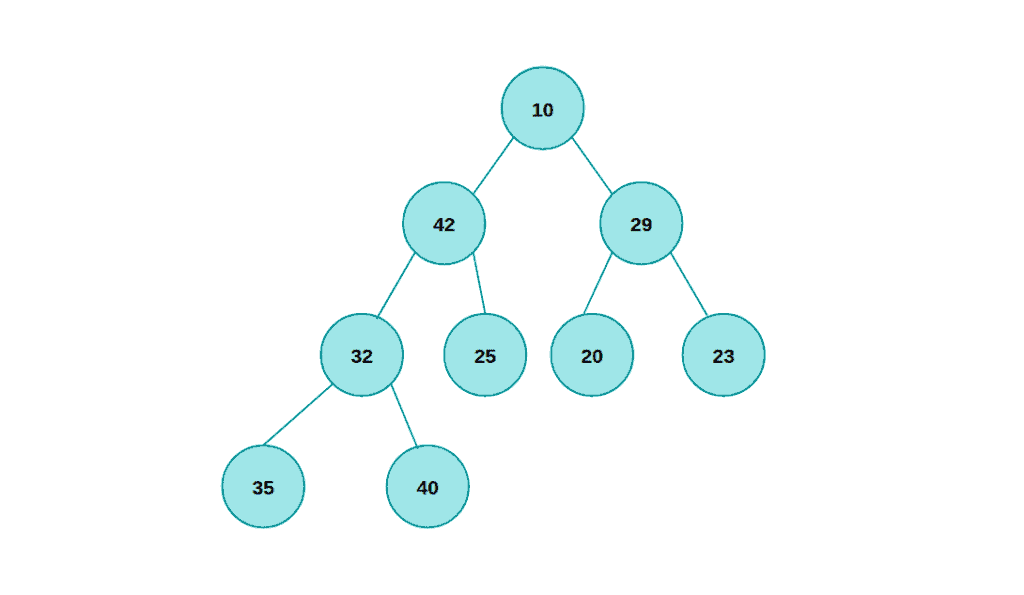
First of all, let’s look at heap’s definition and characteristics. The min-max heap is a complete binary tree with both traits of min heap and max heap:
首先,我们来看看堆的定义和特征。最小-最大堆是一个完整的二叉树,具有最小堆和最大堆两种特征。
As we can see above, each node at an even level in the tree is less than all of its descendants, while each node at an odd level in the tree is greater than all of its descendants, where the root is at level zero.
正如我们在上面看到的,树中偶数层的每个节点都小于其所有的子节点,而树中奇数层的每个节点都大于其所有的子节点,其中根处于零层。
Each node in the min-max heap has a data member that is usually called a key. The root has the smallest key in the min-max heap, and one of the two nodes in the second level is the greatest key. For each node like X in a min-max heap:
最小-最大堆中的每个节点都有一个数据成员,通常被称为键。根在最小最大堆中具有最小的键,第二层中的两个节点之一是最大的键。对于min-max堆中的每个像X的节点。
- If X is on a min (or even) level, then X.key is the minimum key among all keys in the subtree with root X
- If X is on a max (or odd) level, then X.key is the maximum key among all keys in the subtree with root X
Like min-heap or max-heap, insertion and deletion can occur in the time complexity of O(logN).
与min-heap或max-heap一样,插入和删除可以在O(logN)的时间复杂度中发生。
3. Implementation in Java
3.用Java实现
Let’s start with a simple class that represents our min-max heap:
让我们从一个简单的类开始,它代表我们的最小-最大堆。
public class MinMaxHeap<T extends Comparable<T>> {
private List<T> array;
private int capacity;
private int indicator;
}As we can see above, we use an indicator to figure out the last item index added to the array. But before we continue, we need to remember that the array index starts from zero, but we assume the index starts from one in a heap.
正如我们在上面看到的,我们使用一个指示器来计算出最后一个添加到数组中的项目索引。但是在我们继续之前,我们需要记住数组索引从0开始,但是我们假设在堆中索引从1开始。
We can find the index of left and right children using the following methods:
我们可以用以下方法找到左右两个孩子的索引。
private int getLeftChildIndex(int i) {
return 2 * i;
}
private int getRightChildIndex(int i) {
return ((2 * i) + 1);
}Likewise, we can find the index of parent and grandparent of the item in the array by the following code:
同样地,我们可以通过以下代码找到数组中项目的父系和祖系的索引。
private int getParentIndex(int i) {
return i / 2;
}
private int getGrandparentIndex(int i) {
return i / 4;
}Now, let’s continue with complete our simple min-max heap class:
现在,让我们继续完成我们简单的最小-最大堆类。
public class MinMaxHeap<T extends Comparable<T>> {
private List<T> array;
private int capacity;
private int indicator;
MinMaxHeap(int capacity) {
array = new ArrayList<>();
this.capacity = capacity;
indicator = 1;
}
MinMaxHeap(List<T> array) {
this.array = array;
this.capacity = array.size();
this.indicator = array.size() + 1;
}
}We can create an instance of the min-max heap in two ways here. First, we initiate an array with an ArrayList and specific capacity, and second, we make a min-max heap from the existing array.
在这里,我们可以通过两种方式创建一个最小最大堆的实例。首先,我们启动一个具有ArrayList和特定容量的数组,其次,我们从现有数组中制作一个最小最大堆。
Now, let’s discuss operations on our heap.
现在,让我们来讨论对我们的堆的操作。
3.1. Create
3.1.创建
Let’s first look at building a min-max heap from an existing array. Here we use Floyd’s algorithm with some adaption like the Heapify algorithm:
让我们首先看看如何从一个现有的数组中建立一个最小-最大堆。在这里,我们使用Floyd的算法,并进行一些调整,如Heapify算法。
public List<T> create() {
for (int i = Math.floorDiv(array.size(), 2); i >= 1; i--) {
pushDown(array, i);
}
return array;
}Let’s see what exactly happened in the above code by take a look closer to pushDown in the following code:
让我们看看上面的代码到底发生了什么,仔细看看下面代码中的pushDown。
private void pushDown(List<T> array, int i) {
if (isEvenLevel(i)) {
pushDownMin(array, i);
} else {
pushDownMax(array, i);
}
}As we can see, for all even levels, we check array items with pushDownMin. This algorithm is like heapify-down that we’ll use for removeMin and removeMax:
我们可以看到,对于所有的偶数级,我们用pushDownMin来检查数组项。这个算法就像我们将用于removeMin和removeMax的heapify-down。
private void pushDownMin(List<T> h, int i) {
while (getLeftChildIndex(i) < indicator) {
int indexOfSmallest = getIndexOfSmallestChildOrGrandChild(h, i);
//...
i = indexOfSmallest;
}
}First, we find the index of the smallest child or grandchild of the ‘i’ element. Then we proceed according to the following conditions.
首先,我们找到’i’元素最小的子代或孙代的索引。然后我们按照以下条件进行。
If the smallest child or grandchild is not less than the current element, we break. In other words, the current arranges of elements are like min-heap:
如果最小的子代或孙代不小于当前的元素,我们就中断。换句话说,当前元素的排列就像min-heap:。
if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
//...
} else {
break;
}If the smallest child or grandchild is smaller than the current element, we swap it with its parent or grandparent:
如果最小的子代或孙代元素比当前元素小,我们就把它与它的父代或祖代元素交换:。
if (getParentIndex(getParentIndex(indexOfSmallest)) == i) {
if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
swap(indexOfSmallest - 1, i - 1, h);
if (h.get(indexOfSmallest - 1)
.compareTo(h.get(getParentIndex(indexOfSmallest) - 1)) > 0) {
swap(indexOfSmallest - 1, getParentIndex(indexOfSmallest) - 1, h);
}
}
} else if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
swap(indexOfSmallest - 1, i - 1, h);
}We’ll continue the above operations until found a child for the element ‘i’.
我们将继续上述操作,直到为元素’i’找到一个孩子。
Now, Let’s see how getIndexOfSmallestChildOrGrandChild works. It’s pretty easy! First, we assume the left child has the smallest value then compare it with others:
现在,让我们看看getIndexOfSmallestChildOrGrandChild是如何工作的。这很简单!首先,我们假设左边的孩子有最小的值,然后与其他孩子比较。
private int getIndexOfSmallestChildOrGrandChild(List<T> h, int i) {
int minIndex = getLeftChildIndex(i);
T minValue = h.get(minIndex - 1);
// rest of the implementation
}In each step, if the index is greater than the indicator, the last minimum value found is the answer.
在每一步中,如果指数大于指标,最后找到的最小值就是答案。
For example, let’s compare min-value with the right child:
例如,让我们将min-value与右边的孩子进行比较。
if (getRightChildIndex(i) < indicator) {
if (h.get(getRightChildIndex(i) - 1).compareTo(minValue) < 0) {
minValue = h.get(getRightChildIndex(i));
minIndex = getRightChildIndex(i);
}
} else {
return minIndex;
}Now, let’s create a test to verify that make a min-max heap from an unordered array works fine:
现在,让我们创建一个测试来验证从一个无序数组中制作一个最小-最大堆的工作是否正常。
@Test
public void givenUnOrderedArray_WhenCreateMinMaxHeap_ThenIsEqualWithMinMaxHeapOrdered() {
List<Integer> list = Arrays.asList(34, 12, 28, 9, 30, 19, 1, 40);
MinMaxHeap<Integer> minMaxHeap = new MinMaxHeap<>(list);
minMaxHeap.create();
Assert.assertEquals(List.of(1, 40, 34, 9, 30, 19, 28, 12), list);
}The algorithm for pushDownMax is identical to that for pushDownMin, but with all of the comparison, operators reversed.
pushDownMax的算法与pushDownMin的算法相同,但所有的比较、运算符都相反。。
3.2. Insert
3.2 插入
Let’s see how to add an element to a min-max Heap:
让我们看看如何将一个元素添加到最小-最大堆中。
public void insert(T item) {
if (isEmpty()) {
array.add(item);
indicator++;
} else if (!isFull()) {
array.add(item);
pushUp(array, indicator);
indicator++;
} else {
throw new RuntimeException("invalid operation !!!");
}
}First, we check the heap is empty or not. If the heap is empty, we append the new element and increase the indicator. Otherwise, the new element that added may change the order of the min-max heap, So we need to adjust the heap with pushUp:
首先,我们检查堆是否为空。如果堆是空的,我们追加新的元素并增加指标。否则,添加的新元素可能会改变最小-最大堆的顺序,所以我们需要用pushUp调整堆。
private void pushUp(List<T>h,int i) {
if (i != 1) {
if (isEvenLevel(i)) {
if (h.get(i - 1).compareTo(h.get(getParentIndex(i) - 1)) < 0) {
pushUpMin(h, i);
} else {
swap(i - 1, getParentIndex(i) - 1, h);
i = getParentIndex(i);
pushUpMax(h, i);
}
} else if (h.get(i - 1).compareTo(h.get(getParentIndex(i) - 1)) > 0) {
pushUpMax(h, i);
} else {
swap(i - 1, getParentIndex(i) - 1, h);
i = getParentIndex(i);
pushUpMin(h, i);
}
}
}As we can see above, the new element compares its parent, then:
正如我们在上面看到的,新元素比较了它的父元素,然后。
- If it’s found to be less (greater) than the parent, then it’s definitely less (greater) than all other elements on max (min) levels that are on the path to the root of the heap
- The path from the new element to the root (considering only min/max levels) should be in a descending (ascending) order as it was before the insertion. So, we need to make a binary insertion of the new element into this sequence
Now, Let’s take a look at the pushUpMin as is following:
现在,让我们来看看pushUpMin,如下所示。
private void pushUpMin(List<T> h , int i) {
while(hasGrandparent(i) && h.get(i - 1)
.compareTo(h.get(getGrandparentIndex(i) - 1)) < 0) {
swap(i - 1, getGrandparentIndex(i) - 1, h);
i = getGrandparentIndex(i);
}
}Technically, it’s simpler to swap the new element with its parent while the parent is greater. Also, pushUpMax identical to pushUpMin, but with all of the comparison, operators reversed.
从技术上讲,当父元素较大时,将新元素与它的父元素进行交换是比较简单的。另外,pushUpMax与pushUpMin相同,但所有的比较和操作都是相反的。
Now, Let’s create a test to verify that insert a new element into a min-max Heap works fine:
现在,让我们创建一个测试来验证在最小-最大堆中插入一个新元素的工作是否正常。
@Test
public void givenNewElement_WhenInserted_ThenIsEqualWithMinMaxHeapOrdered() {
MinMaxHeap<Integer> minMaxHeap = new MinMaxHeap(8);
minMaxHeap.insert(34);
minMaxHeap.insert(12);
minMaxHeap.insert(28);
minMaxHeap.insert(9);
minMaxHeap.insert(30);
minMaxHeap.insert(19);
minMaxHeap.insert(1);
minMaxHeap.insert(40);
Assert.assertEquals(List.of(1, 40, 28, 12, 30, 19, 9, 34),
minMaxHeap.getMinMaxHeap());
}3.3. Find Min
3.3. 找到最小值
The main element in a min-max heap is always located at the root, so we can find it in time complexity O(1):
最小-最大堆中的主要元素总是位于根部,所以我们可以在时间复杂度为O(1)的情况下找到它。
public T min() {
if (!isEmpty()) {
return array.get(0);
}
return null;
}3.4. Find Max
3.4 找到最大
The max element in a min-max heap it’s always located first odd level, so we can find it in time complexity O(1) with a simple comparison:
最小-最大堆中的最大元素总是位于第一个奇数层,所以我们可以通过一个简单的比较在时间复杂度为O(1)的情况下找到它。
public T max() {
if (!isEmpty()) {
if (indicator == 2) {
return array.get(0);
}
if (indicator == 3) {
return array.get(1);
}
return array.get(1).compareTo(array.get(2)) < 0 ? array.get(2) : array.get(1);
}
return null;
}3.5. Remove Min
3.5.移除最小值
In this case, we’ll find the min element, then replace it with the last element of the array:
在这种情况下,我们将找到最小的元素,然后用数组的最后一个元素替换它。
public T removeMin() {
T min = min();
if (min != null) {
if (indicator == 2) {
array.remove(indicator--);
return min;
}
array.set(0, array.get(--indicator - 1));
array.remove(indicator - 1);
pushDown(array, 1);
}
return min;
}3.6. Remove Max
3.6.删除最大值。
Removing the max element is the same as remove min, with the only change that we find the index of the max element then call pushDown:
删除max元素和删除min元素是一样的,唯一的变化是我们找到max元素的索引然后调用pushDown。
public T removeMax() {
T max = max();
if (max != null) {
int maxIndex;
if (indicator == 2) {
maxIndex = 0;
array.remove(--indicator - 1);
return max;
} else if (indicator == 3) {
maxIndex = 1;
array.remove(--indicator - 1);
return max;
} else {
maxIndex = array.get(1).compareTo(array.get(2)) < 0 ? 2 : 1;
}
array.set(maxIndex, array.get(--indicator - 1));
array.remove(indicator - 1);
pushDown(array, maxIndex + 1);
}
return max;
}4. Conclusion
4.总结
In this tutorial, we’ve seen implementing a min-max heap in Java and exploring some of the most common operations.
在本教程中,我们已经看到了在Java中实现最小-最大堆,并探索了一些最常见的操作。
First, we learned what exactly a min-max heap is, including some of the most common features. Then, we saw how to create, insert, find-min, find-max, remove-min, and remove-max items in our min-max heap implementation.
首先,我们了解了什么是最小-最大堆,包括一些最常见的特征。然后,我们看到了如何在我们的最小最大堆实现中创建、插入、查找最小、查找最大、删除最小和删除最大项目。
As usual, all the examples used in this article are available over on GitHub.
像往常一样,本文中使用的所有例子都可以在GitHub上找到。