1. Introduction
1.绪论
In this tutorial, we’ll introduce the AVL Tree and we’ll look at algorithms for inserting, deleting, and searching for values.
在本教程中,我们将介绍AVL树,我们将研究插入、删除和搜索数值的算法。
2. What Is AVL Tree?
2.什么是AVL树?
The AVL Tree, named after its inventors Adelson-Velsky and Landis, is a self-balancing binary search tree (BST).
AVL树以其发明者Adelson-Velsky和Landis的名字命名,是一种自平衡的二进制搜索树(BST)。
A self-balancing tree is a binary search tree that balances the height after insertion and deletion according to some balancing rules.
自平衡树是一种二进制搜索树,它在插入和删除后根据一些平衡规则平衡高度。。
The worst-case time complexity of a BST is a function of the height of the tree. Specifically, the longest path from the root of the tree to a node. For a BST with N nodes, let’s say that that every node has only zero or one child. Therefore its height equals N, and the search time in the worst case is O(N). So our main goal in a BST is to keep the maximum height close to log(N).
BST的最坏情况下的时间复杂度是树的高度的一个函数。具体来说,就是从树根到一个节点的最长路径而言。对于一个有N个节点的BST,我们假设每个节点只有0或1个孩子。因此,它的高度等于N,在最坏的情况下,搜索时间是O(N)。所以我们在BST中的主要目标是保持最大高度接近log(N)。
The balance factor of node N is height(right(N)) – height(left(N)). In an AVL Tree, the balance factor of a node could be only one of 1, 0, or -1 values.
节点N的平衡系数是height(right(N)) – height(left(N))。在AVL树中,一个节点的平衡系数只能是1、0或-1中的一个值。
Let’s define a Node object for our tree:
让我们为我们的树定义一个Node对象。
public class Node {
int key;
int height;
Node left;
Node right;
...
}Next, let’s define the AVLTree:
接下来,我们来定义AVLTree。
public class AVLTree {
private Node root;
void updateHeight(Node n) {
n.height = 1 + Math.max(height(n.left), height(n.right));
}
int height(Node n) {
return n == null ? -1 : n.height;
}
int getBalance(Node n) {
return (n == null) ? 0 : height(n.right) - height(n.left);
}
...
}3. How to Balance an AVL Tree?
3.如何平衡一棵AVL树?
The AVL Tree checks the balance factor of its nodes after the insertion or deletion of a node. If the balance factor of a node is greater than one or less than -1, the tree rebalances itself.
AVL树在插入或删除一个节点后会检查其节点的平衡系数。如果一个节点的平衡系数大于1或小于-1,树就会进行自我平衡。
There are two operations to rebalance a tree:
有两种操作来重新平衡一棵树。
- right rotation and
- left rotation.
3.1. Right Rotation
3.1.右旋转
Let’s start with the right rotation.
让我们从右转开始。
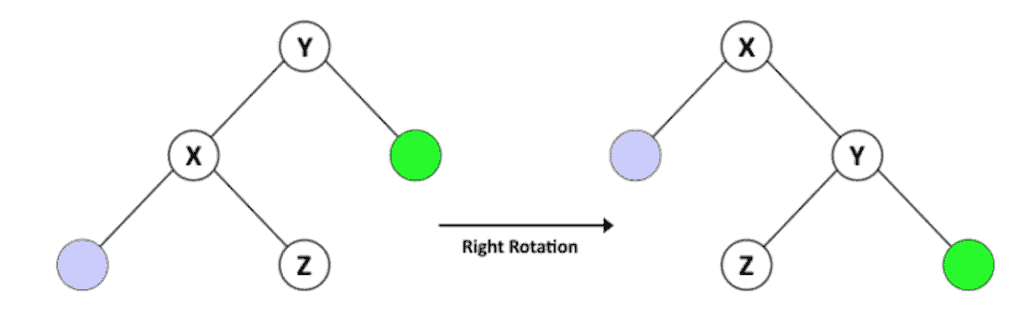
Assume we have a BST called T1, with Y as the root node, X as the left child of Y, and Z as the right child of X. Given the characteristics of a BST, we know that X < Z < Y.
假设我们有一个叫T1的BST,Y是根节点,X是Y的左子,Z是X的右子,鉴于BST的特点,我们知道X<Z<Y。
After a right rotation of Y, we have a tree called T2 with X as the root and Y as the right child of X and Z as the left child of Y. T2 is still a BST because it keeps the order X < Z < Y.
对Y进行右旋转后,我们有一棵叫做T2的树,X是根,Y是X的右子,Z是Y的左子。T2仍然是一棵BST,因为它保持了X < Z < Y的顺序。
Let’s take a look at the right rotation operation for our AVLTree:
让我们来看看我们的AVLTree的正确旋转操作。
Node rotateRight(Node y) {
Node x = y.left;
Node z = x.right;
x.right = y;
y.left = z;
updateHeight(y);
updateHeight(x);
return x;
}3.2. Left Rotation Operation
3.2.左旋操作
We also have a left rotation operation.
我们也有一个左旋操作。
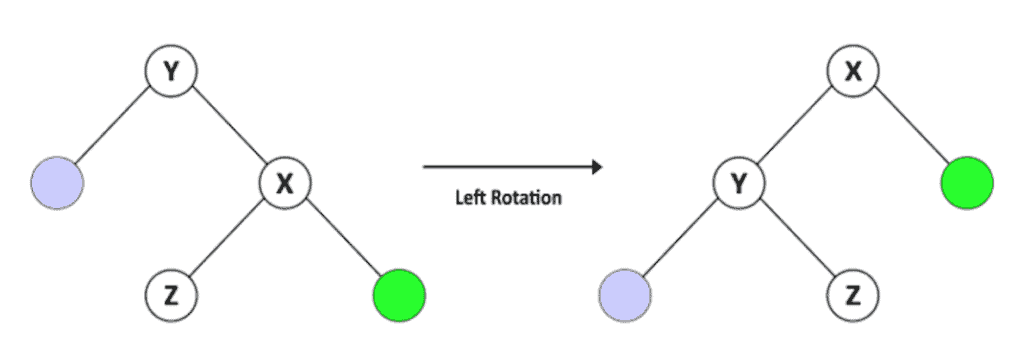
Assume a BST called T1, with Y as the root node, X as the right child of Y, and Z as the left child of X. Given this, we know that Y < Z < X.
假设有一个叫T1的BST,Y是根节点,X是Y的右子,Z是X的左子,鉴于此,我们知道Y<Z<X。
After a left rotation of Y, we have a tree called T2 with X as the root and Y as the left child of X and Z as the right child of Y. T2 is still a BST because it keeps the order Y < Z < X.
对Y进行左旋转后,我们有一棵叫做T2的树,X是根,Y是X的左子,Z是Y的右子。T2仍然是一棵BST,因为它保持了Y < Z < X的顺序。
Let’s take a look at the left rotation operation for our AVLTree:
让我们看一下我们的AVLTree的左旋操作。
Node rotateLeft(Node y) {
Node x = y.right;
Node z = x.left;
x.left = y;
y.right = z;
updateHeight(y);
updateHeight(x);
return x;
}3.3. Rebalancing Techniques
3.3.再平衡技术
We can use the right rotation and left rotation operations in more complex combinations to keep the AVL Tree balanced after any change in its nodes. In an unbalanced structure, at least one node has a balance factor equal to 2 or -2. Let’s see how we can balance the tree in these situations.
我们可以在更复杂的组合中使用右旋转和左旋转操作来在AVL树的节点发生任何变化后保持平衡。在一个不平衡的结构中,至少有一个节点的平衡系数等于2或-2。让我们看看在这些情况下,我们如何平衡树。
When the balance factor of node Z is 2, the subtree with Z as the root is in one of these two states, considering Y as the right child of Z.
当节点Z的平衡系数为2时,以Z为根的子树处于这两种状态中的一种,认为Y是Z的右侧子。
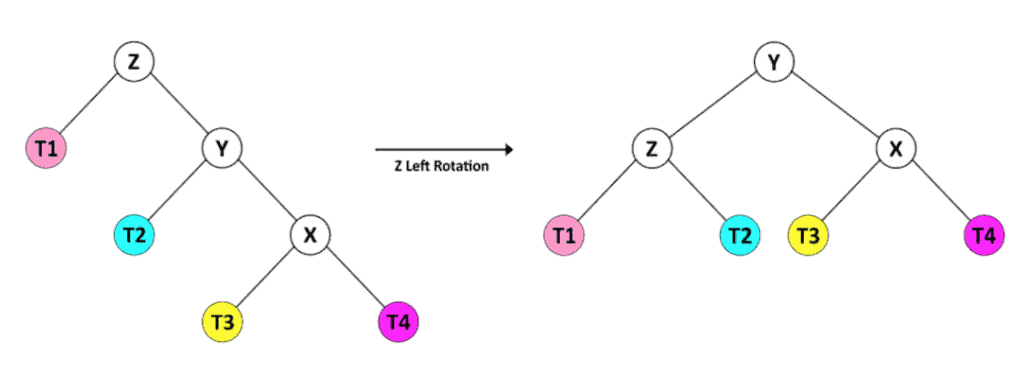
For the first case, the height in the right child of Y (X) is greater than the hight of the left child (T2). We can rebalance the tree easily by a left rotation of Z.
对于第一种情况,Y的右边的孩子(X)的高度比左边的孩子(T2)的高度大。我们可以通过对Z的左旋转来轻松地重新平衡树。
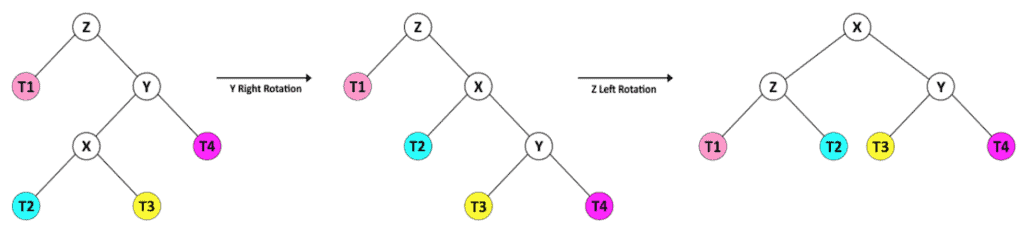
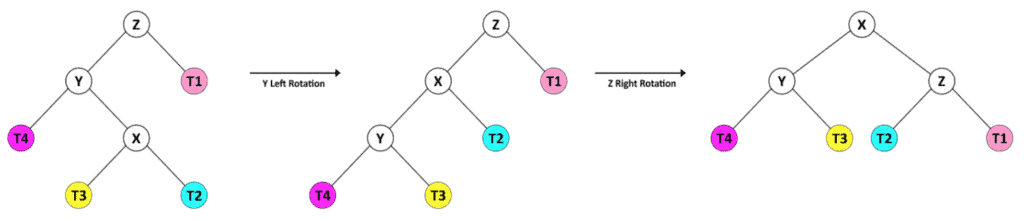
For the second case, the height of the right child of Y (T4) is less than the height of the left child (X). This situation needs a combination of rotation operations.
对于第二种情况,Y的右子(T4)的高度小于左子(X)的高度。这种情况需要旋转操作的组合。
In this case, we first rotate Y to the right, so the tree gets in the same shape as the previous case. Then we can rebalance the tree by a left rotation of Z.
在这种情况下,我们首先将Y向右旋转,这样树的形状就和之前的情况一样了。然后我们可以通过Z的左旋转来重新平衡树。
Also, when the balance factor of node Z is -2, its subtree is in one of these two states, so we consider Z as the root and Y as its left child.
另外,当节点Z的平衡系数为-2时,它的子树处于这两种状态之一,所以我们认为Z是根,Y是它的左子。
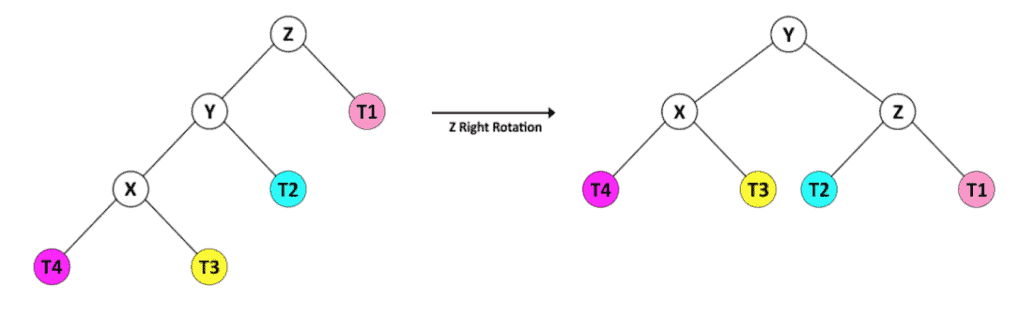
The height in the left child of Y is greater than that of its right child, so we balance the tree with the right rotation of Z.
Y的左边孩子的高度大于其右边孩子的高度,所以我们用Z的右旋转来平衡树。
Or in the second case, the right child of Y has a greater height than its left child.
或者在第二种情况下,Y的右边的孩子比其左边的孩子有更大的高度。
So, first of all, we transform it into the former shape with a left rotation of Y, then we balance the tree with the right rotation of Z.
因此,首先,我们用Y的左旋转将其转化为前一种形状,然后用Z的右旋转来平衡树。
Let’s take a look at the rebalance operation for our AVLTree:
让我们看看我们的AVLTree的再平衡操作。
Node rebalance(Node z) {
updateHeight(z);
int balance = getBalance(z);
if (balance > 1) {
if (height(z.right.right) > height(z.right.left)) {
z = rotateLeft(z);
} else {
z.right = rotateRight(z.right);
z = rotateLeft(z);
}
} else if (balance < -1) {
if (height(z.left.left) > height(z.left.right))
z = rotateRight(z);
else {
z.left = rotateLeft(z.left);
z = rotateRight(z);
}
}
return z;
}We’ll use rebalance after inserting or deleting a node for all the nodes in the path from the changed node to the root.
在插入或删除一个节点后,我们将使用rebalance来处理从被改变的节点到根的路径中的所有节点。
4. Insert a Node
4.插入一个节点
When we’re going to insert a key in the tree, we have to locate its proper position to pass the BST rules. So we start from the root and compare its value with the new key. If the key is greater, we continue to the right — otherwise, we go to the left child.
当我们要在树中插入一个键时,我们必须找到它的适当位置以通过BST规则。所以我们从根部开始,将其值与新的键进行比较。如果键值较大,我们就继续向右移动–否则,我们就去找左边的孩子。
Once we find the proper parent node, then we add the new key as a node to left or right, depending on the value.
一旦我们找到合适的父节点,那么我们就把新的键作为一个节点添加到左边或右边,这取决于值。
After inserting the node, we have a BST, but it may not be an AVL Tree. Therefore, we check the balance factors and rebalance the BST for all the nodes in the path from the new node to the root.
在插入节点后,我们有一个BST,但它可能不是一个AVL树。因此,我们检查平衡因子,重新平衡从新节点到根路径上的所有节点的BST。
Let’s take a look at the insert operation:
让我们看一下插入操作。
Node insert(Node node, int key) {
if (node == null) {
return new Node(key);
} else if (node.key > key) {
node.left = insert(node.left, key);
} else if (node.key < key) {
node.right = insert(node.right, key);
} else {
throw new RuntimeException("duplicate Key!");
}
return rebalance(node);
}It is important to remember that a key is unique in the tree — no two nodes share the same key.
重要的是要记住,一个键在树中是唯一的–没有两个节点共享相同的键。。
The time complexity of the insert algorithm is a function of the height. Since our tree is balanced, we can assume that time complexity in the worst case is O(log(N)).
插入算法的时间复杂度是高度的一个函数。由于我们的树是平衡的,我们可以假设最坏情况下的时间复杂性是O(log(N))。
5. Delete a Node
5.删除一个节点
To delete a key from the tree, we first have to find it in the BST.
要从树上删除一个键,我们首先要在BST中找到它。
After we find the node (called Z), we have to introduce the new candidate to be its replacement in the tree. If Z is a leaf, the candidate is empty. If Z has only one child, this child is the candidate, but if Z has two children, the process is a bit more complicated.
在我们找到这个节点(称为Z)之后,我们必须引入新的候选者,作为它在树上的替代。如果Z是一个叶子,那么这个候选节点就是空的。如果Z只有一个孩子,这个孩子就是候选人,但如果Z有两个孩子,这个过程就有点复杂了。
Assume the right child of Z called Y. First, we find the leftmost node of the Y and call it X. Then, we set the new value of Z equal to X ‘s value and continue to delete X from Y.
首先,我们找到Y的最左边的节点并称其为X。然后,我们设置Z的新值等于X的值并继续从Y中删除X。
Finally, we call the rebalance method at the end to keep the BST an AVL Tree.
最后,我们在最后调用rebalance方法,使BST保持为AVL树。
Here is our delete method:
这里是我们的删除方法。
Node delete(Node node, int key) {
if (node == null) {
return node;
} else if (node.key > key) {
node.left = delete(node.left, key);
} else if (node.key < key) {
node.right = delete(node.right, key);
} else {
if (node.left == null || node.right == null) {
node = (node.left == null) ? node.right : node.left;
} else {
Node mostLeftChild = mostLeftChild(node.right);
node.key = mostLeftChild.key;
node.right = delete(node.right, node.key);
}
}
if (node != null) {
node = rebalance(node);
}
return node;
}The time complexity of the delete algorithm is a function of the height of the tree. Similar to the insert method, we can assume that time complexity in the worst case is O(log(N)).
删除算法的时间复杂度是树的高度的一个函数。与插入法类似,我们可以假设最坏情况下的时间复杂度为O(log(N))。
6. Search for a Node
6.搜索一个节点
Searching for a node in an AVL Tree is the same as with any BST.
在AVL树中搜索一个节点,与任何BST的搜索方式相同。
Start from the root of the tree and compare the key with the value of the node. If the key equals the value, return the node. If the key is greater, search from the right child, otherwise continue the search from the left child.
从树的根部开始,比较键和节点的值。如果键等于值,返回该节点。如果键值较大,从右边的子节点开始搜索,否则从左边的子节点继续搜索。
The time complexity of the search is a function of the height. We can assume that time complexity in the worst case is O(log(N)).
搜索的时间复杂度是一个高度的函数。我们可以假设最坏情况下的时间复杂度是O(log(N))。
Let’s see the sample code:
让我们看看示例代码。
Node find(int key) {
Node current = root;
while (current != null) {
if (current.key == key) {
break;
}
current = current.key < key ? current.right : current.left;
}
return current;
}7. Conclusion
7.结语
In this tutorial, we have implemented an AVL Tree with insert, delete, and search operations.
在本教程中,我们实现了一个具有插入、删除和搜索操作的AVL树。
As always, you can find the code over on Github.
一如既往,你可以在Github上找到代码,。