1. Overview

1.概述

Trees are one of the most important data structures in computer science. We’re usually interested in a balanced tree, because of its valuable properties. Their structure allows performing operations like queries, insertions, deletions in logarithmic time.

树是计算机科学中最重要的数据结构之一。我们通常对平衡树感兴趣，因为它具有宝贵的特性。它们的结构允许在对数时间内执行查询、插入、删除等操作。

In this tutorial, we’re going to learn how to determine if a binary tree is balanced.

在本教程中，我们将学习如何确定一棵二叉树是否平衡。

2. Definitions

2.定义

First, let’s introduce a few definitions in order to make sure we’re on the same page:

首先，让我们介绍几个定义，以确保我们在同一页上。

A binary tree – a kind of a tree where every node has zero, one or two children
A height of a tree – a maximum distance from a root to a leaf (same as the depth of the deepest leaf)
A balanced tree – a kind of a tree where for every subtree the maximum distance from the root to any leaf is at most bigger by one than the minimum distance from the root to any leaf

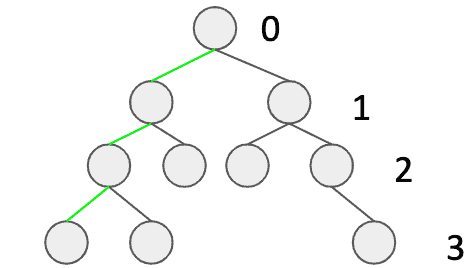
We can find an example of a balanced binary tree below. Three green edges are a simple visualization of how to determine the height, while the numbers indicate the level.

我们可以在下面找到一个平衡二叉树的例子。三条绿色的边是一个简单的可视化，说明如何确定高度，而数字表示水平。

3. Domain Objects

3.领域对象

So, let’s start with a class for our tree:

因此，让我们从为我们的树建立一个类开始。

public class Tree {
    private int value;
    private Tree left;
    private Tree right;

    public Tree(int value, Tree left, Tree right) {
        this.value = value;
        this.left = left;
        this.right = right;
    }
}

For the sake of simplicity, let’s say each node has an integer value. Note, that if left and right trees are null, then it means our node is a leaf.

为了简单起见，我们说每个节点有一个整数值。注意，如果左边和右边的树是null,，那么就意味着我们的节点是一个叶子。

Before we introduce our primary method let’s see what it should return:

在我们介绍我们的主要方法之前，让我们看看它应该返回什么。

private class Result {
    private boolean isBalanced;
    private int height;

    private Result(boolean isBalanced, int height) {
        this.isBalanced = isBalanced;
        this.height = height;
    }
}

Thus for every single call, we’ll have information about height and balance.

因此，对于每一个电话，我们都会有关于高度和平衡的信息。

4. Algorithm

4.算法

Having a definition of a balanced tree, we can come up with an algorithm. What we need to do is to check the desired property for every node. It can be achieved easily with recursive depth-first search traversal.

有了平衡树的定义，我们就可以想出一个算法了。我们需要做的是为每个节点检查所需的属性。这可以通过递归深度优先搜索遍历轻松实现。

Now, our recursive method will be invoked for every node. Additionally, it will keep track of the current depth. Each call will return information about height and balance.

现在，我们的递归方法将对每个节点进行调用。此外，它还将跟踪当前的深度。每次调用将返回有关高度和平衡的信息。

Now, let’s take a look at our depth-first method:

现在，让我们来看看我们的深度优先方法。

private Result isBalancedRecursive(Tree tree, int depth) {
    if (tree == null) {
        return new Result(true, -1);
    }

    Result leftSubtreeResult = isBalancedRecursive(tree.left(), depth + 1);
    Result rightSubtreeResult = isBalancedRecursive(tree.right(), depth + 1);

    boolean isBalanced = Math.abs(leftSubtreeResult.height - rightSubtreeResult.height) <= 1;
    boolean subtreesAreBalanced = leftSubtreeResult.isBalanced && rightSubtreeResult.isBalanced;
    int height = Math.max(leftSubtreeResult.height, rightSubtreeResult.height) + 1;

    return new Result(isBalanced && subtreesAreBalanced, height);
}

First, we need to consider the case if our node is null: we’ll return true (which means the tree is balanced) and -1 as a height.

首先，我们需要考虑如果我们的节点是null的情况：我们将返回true（这意味着树是平衡的）和-1作为高度。

Then, we make two recursive calls for the left and the right subtree, keeping the depth up to date.

然后，我们对左边和右边的子树进行两次递归调用，保持最新的深度。

At this point, we have calculations performed for children of a current node. Now, we have all the required data to check balance:

在这一点上，我们已经对当前节点的子女进行了计算。现在，我们有所有需要的数据来检查平衡。

the isBalanced variable checks the height for children, and
substreesAreBalanced indicates if the subtrees are both balanced as well

Finally, we can return information about balance and height. It might be also a good idea to simplify the first recursive call with a facade method:

最后，我们可以返回有关平衡和高度的信息。用一个facade方法简化第一个递归调用可能也是一个好主意。

public boolean isBalanced(Tree tree) {
    return isBalancedRecursive(tree, -1).isBalanced;
}

5. Summary

5.摘要

In this article, we’ve discussed how to determine if a binary tree is balanced. We’ve explained a depth-first search approach.

在这篇文章中，我们讨论了如何确定一棵二叉树是否是平衡的。我们解释了一种深度优先搜索方法。

As usual, the source code with tests is available over on GitHub.

像往常一样，带有测试的源代码可以在GitHub上找到。