1. Introduction

1.绪论

Java provides some primitives, such as int or long, to perform integer operations. But sometimes, we need to store numbers, which overflow the available limits for those data types.

Java提供了一些基元，如int或long，以执行整数操作。但有时，我们需要存储数字，这些数字超出了这些数据类型的可用限制。

In this tutorial, we’ll look deeper into the BigInteger class. We’ll check its structure by looking into the source code and answer the question – how is it possible to store large numbers outside the limit of available primitive data types?

在本教程中，我们将深入研究BigInteger类。我们将通过查看源代码来检查其结构，并回答这个问题–h如何在可用的原始数据类型的限制之外存储大数？

2. BigInteger Class

2.BigInteger类

As we know, the BigInteger class is used for mathematical operations which involve very big integer calculations larger than the primitive long type. It represents immutable arbitrary-precision integers.

正如我们所知，BigInteger类用于涉及比原始long类型更大的非常大的整数计算的数学运算。它代表不可改变的任意精度的整数。

Before going further, let’s remember that in Java all bytes are represented in the two’s-complement system using the big-endian notation. It stores the most significant byte of a word at the smallest memory address (the lowest index). Moreover, the first bit of the byte is also a sign bit. Let’s inspect example byte values:

在进一步讨论之前，让我们记住，在Java中，所有的字节都用two’s-complement系统表示，使用big-endian符号。它将一个字的最重要的字节存储在最小的内存地址（最低索引）。此外，字节的第一位也是一个符号位。让我们检查一下字节值的例子。

1000 0000 represents -128
0111 1111 represents 127
1111 1111 represents -1

So now, let’s check the source code and explain how it stores given numbers exceeding available primitives limits.

那么现在，让我们检查一下源代码，解释一下它是如何存储超过可用基元限制的给定数字的。

2.1. int signum

2.1int signum

The signum property determines the sign of the BigInteger. Three integer values represent the value’s sign: -1 for negative, 0 for zero, 1 for positive numbers:

signum属性决定了BigInteger的符号。三个整数值代表该值的符号。-1代表负数，0代表零，1代表正数。

assertEquals(1, BigInteger.TEN.signum());
assertEquals(-1, BigInteger.TEN.negate().signum());
assertEquals(0, BigInteger.ZERO.signum());

Let’s be aware that BigInteger.ZERO must have the signum of 0 due to the magnitude array. This value ensures that there is exactly one representation for each BigInteger value.

我们要知道，BigInteger.ZERO 由于幅度数组的原因，必须具有0的signum。这个值可以确保每个BigInteger值都有精确的表示。

2.2. int[] mag

2.2.int[] core

All the magic of the BigInteger class starts with the mag property. It stores the given value in an array using the binary representation, which allows omitting primitive data types limits.

BigInteger类的所有神奇之处在于mag属性。它使用二进制表示法将给定值存储在一个数组中，这允许省略原始数据类型的限制。

Moreover, the BigInteger groups them in 32-bit portions – a set of four bytes. Due to this, the magnitude inside the class definition is declared as the int array:

此外，BigInteger 将它们分组为32位的部分 – 一组四个字节。由于这个原因，类定义里面的量级被声明为int数组。

int[] mag;

This array holds the magnitude of the given value in big-endian notation. The zeroth element of this array is the most significant int of the magnitude. Let’s check it using BigInteger(byte[] bytes):

这个数组以big-endian记数法保存给定值的大小。这个数组的第2个元素是幅度中最重要的int。让我们用BigInteger(byte[] bytes)来检查它。

assertEquals(new BigInteger("1"), new BigInteger(new byte[]{0b1}))
assertEquals(new BigInteger("2"), new BigInteger(new byte[]{0b10}))
assertEquals(new BigInteger("4"), new BigInteger(new byte[]{0b100}))

This constructor translates a given byte array containing the two’s-complement binary representation into the value.

这个构造函数将一个给定的包含二进制补码的字节数组翻译成数值。

Since there’s a sign-magnitude variable (signum), we don’t use the first bit as a sign bit of the value. Let’s quickly check it:

由于有一个符号量变量（signum），我们不使用第一位作为值的符号位。让我们快速检查一下。

byte[] bytes = { -128 }; // 1000 0000
assertEquals(new BigInteger("128"), new BigInteger(1, bytes));
assertEquals(new BigInteger("-128"), new BigInteger(-1, bytes));

We created two different values using the BigInteger(int signum, byte[] magnitude) constructor. It translates the sign-magnitude representation into the BigInteger. We reused the same bytes array, changing only a sign value.

我们使用BigInteger(int signum, byte[] magnitude)构造函数创建两个不同的值。它将符号-幅度表示法转化为BigInteger。我们重新使用了同一个字节数组，只改变了一个符号值。

We can also print the magnitude using the toString(int radix) method:

我们也可以使用toString(int radix)方法来打印量级。

assertEquals("10000000", new BigInteger(1, bytes));
assertEquals("-10000000", new BigInteger(-1, bytes));

Notice that for the negative values, the minus sign is added.

注意，对于负值，要加上减号。

Finally, the magnitude’s most significant int must be non-zero. This implies that the BigInteger.ZERO has a zero-length mag array:

最后，幅度的最重要的int必须是非零。这意味着BigInteger.ZERO有一个零长度的mag阵列。

assertEquals(0, BigInteger.ZERO.bitCount()); 
assertEquals(BigInteger.ZERO, new BigInteger(0, new byte[]{}));

For now, we’ll skip inspecting other properties. They are marked as deprecated due to redundancy, used only as internal cache.

现在，我们将跳过对其他属性的检查。由于冗余，它们被标记为废弃的，只作为内部缓存使用。

Let’s now go straight to the more complex examples and check how the BigInteger stores numbers over the primitive data types.

现在让我们直接进入更复杂的例子，检查BigInteger如何在原始数据类型上存储数字。

3. BigInteger Larger Than Long.MAX_VALUE.

3.BigInteger 大于Long.MAX_VALUE.

As we already know, the long data type is a 64-bit two’s complement integer. The signed long has a minimum value of -2⁶³ (1000 0000 … 0000) and a maximum value of 2⁶³-1 (0111 1111 … 1111). To create a number over those limits, we need to use the BigInteger class.

我们已经知道，long数据类型是一个64位的双补整数。有符号long的最小值为-2⁶³ (1000 0000 … 0000)，最大值为2⁶³-1 (0111 1111 … 1111)。为了创建一个超过这些限制的数字，我们需要使用BigInteger类。

Let’s now create a value larger by one than Long.MAX_VALUE, equal to 2⁶³. According to the information in the previous chapter, it needs to have:

现在让我们创建一个比Long.MAX_VALUE大一的值，等于2⁶³。根据上一章的信息，它需要有。

a signum property set to 1,
a mag array, with 64 bits total, where only the most significant bit set (1000 0000 … 0000).

Firstly, let’s create a BigInteger using the setBit(int n) function:

首先，让我们使用setBit(int n)函数创建一个BigInteger。

BigInteger bi1 = BigInteger.ZERO.setBit(63);
String str = bi1.toString(2);
assertEquals(64, bi1.bitLength());
assertEquals(1, bi1.signum());
assertEquals("9223372036854775808", bi1.toString());
assertEquals(BigInteger.ONE, bi1.substract(BigInteger.valueOf(Long.MAX_VALUE)));

assertEquals(64, str.length());
assertTrue(str.matches("^10{63}$")); // 1000 0000 ... 0000

Remember that in the binary representation system, bits are ordered from right to left, starting from 0. While the BigInteger.ZERO has an empty magnitude array, setting the 63rd bit makes it at the same time the most significant – the zeroth element of the 64 length array. The signum is automatically set to one.

请记住，在二进制表示系统中，比特从右到左排序，从0开始。虽然BigInteger.ZERO有一个空的幅度数组，但设置第63位同时也使它成为最重要的–64个长度数组中的第2个元素。signum被自动设置为1。

On the other hand, the same bit sequence is represented by the Long.MIN_VALUE. Let’s transform this constant into byte[] array and create construct the BigInteger:

另一方面，同样的比特序列由Long.MIN_VALUE表示。让我们把这个常数转换成byte[]数组，并创建构建BigInteger:。

byte[] bytes = ByteBuffer.allocate(Long.BYTES).putLong(Long.MIN_VALUE).array();
BigInteger bi2 = new BigInteger(1, bytes);
assertEquals(bi1, bi2);
...

As we see, both values are equal, so the same pack of assertions applies.

正如我们所看到的，两个值都是相等的，所以同样的一揽子断言也适用。

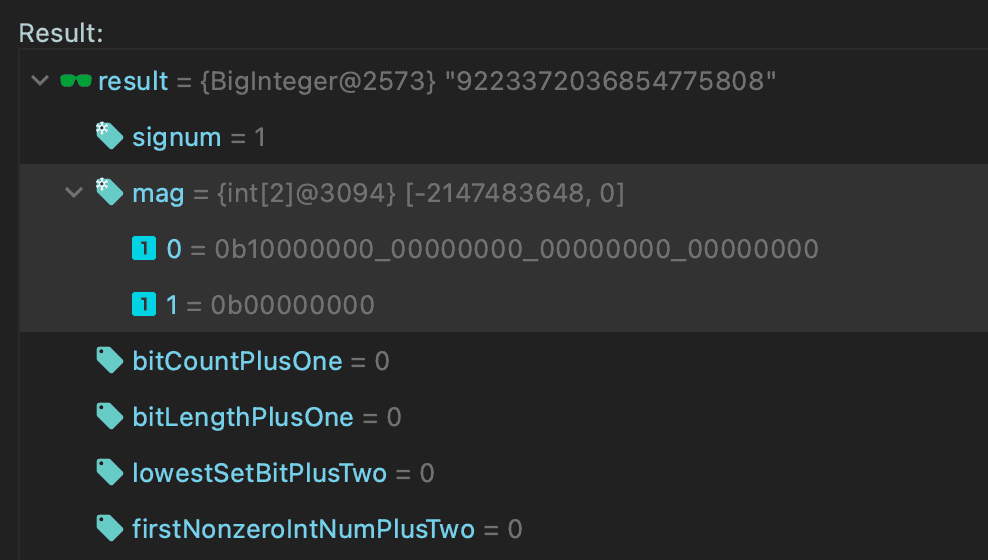
Finally, we can inspect the internal int[] mag variable. Currently, Java doesn’t provide API to get this value, but we can do it by evaluation tool in our debugger:

最后，我们可以检查内部int[] mag变量。目前，Java没有提供API来获取这个值，但我们可以通过调试器中的评估工具来实现。

We store our value in the array using two integers, two packs of 32-bits. The zeroth element is equal to Integer.MIN_VALUE and the other is zero.

我们使用两个整数将我们的值存储在数组中，两个32位的包。第2个元素等于Integer.MIN_VALUE，另一个是0。

4. Conclusion

4.总结

In this quick tutorial, we focused on the implementation details of the BigInteger class. We started by reminding some information about numbers, primitives, and the binary representation rules.

在这个快速教程中，我们着重介绍了BigInteger类的实现细节。我们首先提醒了一些关于数字、基元和二进制表示规则的信息。

Then we inspected the source code of the BigInteger. We checked signum and mag properties. We also learned how the BigInteger stores the given value, allowing us to provide larger numbers than available primitive data types.

然后我们检查了BigInteger的源代码。我们检查了signum和mag属性。我们还了解了BigInteger如何存储给定值，允许我们提供比可用的原始数据类型更大的数字。

As always, we can find all code snippets and tests over on GitHub.

一如既往，我们可以在GitHub上找到所有的代码片段和测试。