1. Overview
1.概述
In this tutorial, we’re going to learn about the Breadth-First Search algorithm, which allows us to search for a node in a tree or a graph by traveling through their nodes breadth-first rather than depth-first.
在本教程中,我们将学习广度优先搜索算法,该算法允许我们通过广度优先而不是深度优先的方式来搜索树或图中的某个节点。
First, we’ll go through a bit of theory about this algorithm for trees and graphs. After that, we’ll dive into the implementations of the algorithms in Java. Finally, we’ll cover their time complexity.
首先,我们将通过一些关于这种树和图的算法的理论。之后,我们将深入探讨算法在Java中的实现。最后,我们将介绍它们的时间复杂性。
2. Breadth-First Search Algorithm
2.广度优先搜索算法
The basic approach of the Breadth-First Search (BFS) algorithm is to search for a node into a tree or graph structure by exploring neighbors before children.
广度优先搜索(BFS)算法的基本方法是通过探索子代之前的邻居来搜索进入树或图结构的节点。
First, we’ll see how this algorithm works for trees. After that, we’ll adapt it to graphs, which have the specific constraint of sometimes containing cycles. Finally, we’ll discuss the performance of this algorithm.
首先,我们将看到这个算法对树是如何工作的。之后,我们将把它改编成图,因为图有一个特定的约束,即有时包含循环。最后,我们将讨论这个算法的性能。
2.1. Trees
2.1.树木
The idea behind the BFS algorithm for trees is to maintain a queue of nodes that will ensure the order of traversal. At the beginning of the algorithm, the queue contains only the root node. We’ll repeat these steps as long as the queue still contains one or more nodes:
树的BFS算法背后的想法是维护一个节点队列,以确保遍历的顺序。在算法的开始,队列只包含根节点。只要队列仍然包含一个或多个节点,我们就会重复这些步骤。
- Pop the first node from the queue
- If that node is the one we’re searching for, then the search is over
- Otherwise, add this node’s children to the end of the queue and repeat the steps
Execution termination is ensured by the absence of cycles. We’ll see how to manage cycles in the next section.
执行终止是由没有循环来保证的。我们将在下一节看到如何管理循环。
2.2. Graphs
2.2 图形
In the case of graphs, we must think of possible cycles in the structure. If we simply apply the previous algorithm on a graph with a cycle, it’ll loop forever. Therefore, we’ll need to keep a collection of the visited nodes and ensure we don’t visit them twice:
在图的情况下,我们必须考虑到结构中可能存在的循环。如果我们简单地在一个有循环的图上应用之前的算法,它将永远循环。因此,我们需要保留一个被访问节点的集合,并确保我们不会访问它们两次。
- Pop the first node from the queue
- Check if the node has already been visited, if so skip it
- If that node is the one we’re searching for, then the search is over
- Otherwise, add it to the visited nodes
- Add this node’s children to the queue and repeat these steps
3. Implementation in Java
3.用Java实现
Now that the theory has been covered, let’s get our hands into the code and implement these algorithms in Java!
现在理论已经讲完了,让我们动手编写代码,在Java中实现这些算法吧!
3.1. Trees
3.1.树木
First, we’ll implement the tree algorithm. Let’s design our Tree class, which consists of a value and children represented by a list of other Trees:
首先,我们要实现树的算法。让我们设计我们的Tree类,它由一个值和由其他Tree的列表表示的子项组成。
public class Tree<T> {
private T value;
private List<Tree<T>> children;
private Tree(T value) {
this.value = value;
this.children = new ArrayList<>();
}
public static <T> Tree<T> of(T value) {
return new Tree<>(value);
}
public Tree<T> addChild(T value) {
Tree<T> newChild = new Tree<>(value);
children.add(newChild);
return newChild;
}
}To avoid creating cycles, children are created by the class itself, based on a given value.
为了避免产生循环,子代是由类本身根据一个给定的值来创建的。
After that, let’s provide a search() method:
之后,让我们提供一个search()方法。
public static <T> Optional<Tree<T>> search(T value, Tree<T> root) {
//...
}As we mentioned earlier, the BFS algorithm uses a queue to traverse the nodes. First of all, we add our root node to this queue:
正如我们前面提到的,BFS算法使用一个队列来遍历节点。首先,我们将我们的根节点添加到这个队列中。
Queue<Tree<T>> queue = new ArrayDeque<>();
queue.add(root);Then, we’ve got to loop while the queue is not empty, and each time we pop out a node from the queue:
然后,我们必须在队列不为空时进行循环,每次都从队列中跳出一个节点。
while(!queue.isEmpty()) {
Tree<T> currentNode = queue.remove();
}If that node is the one we’re searching for, we return it, else we add its children to the queue:
如果该节点是我们要搜索的节点,我们将其返回,否则我们将其子节点添加到队列中。
if (currentNode.getValue().equals(value)) {
return Optional.of(currentNode);
} else {
queue.addAll(currentNode.getChildren());
}Finally, if we visited all the nodes without finding the one we’re searching for, we return an empty result:
最后,如果我们访问了所有的节点而没有找到我们要搜索的那个节点,我们就会返回一个空的结果。
return Optional.empty();Let’s now imagine an example tree structure:
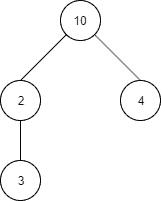
现在让我们想象一个树状结构的例子。
Which translates into the Java code:
这就翻译成了Java代码。
Tree<Integer> root = Tree.of(10);
Tree<Integer> rootFirstChild = root.addChild(2);
Tree<Integer> depthMostChild = rootFirstChild.addChild(3);
Tree<Integer> rootSecondChild = root.addChild(4);Then, if searching for the value 4, we expect the algorithm to traverse nodes with values 10, 2 and 4, in that order:
那么,如果搜索数值4,我们希望该算法能够依次遍历数值为10、2和4的节点。
BreadthFirstSearchAlgorithm.search(4, root)We can verify that with logging the value of the visited nodes:
我们可以通过记录所访问节点的值来验证。
[main] DEBUG c.b.a.b.BreadthFirstSearchAlgorithm - Visited node with value: 10
[main] DEBUG c.b.a.b.BreadthFirstSearchAlgorithm - Visited node with value: 2
[main] DEBUG c.b.a.b.BreadthFirstSearchAlgorithm - Visited node with value: 43.2. Graphs
3.2 图表
That concludes the case of trees. Let’s now see how to deal with graphs. Contrarily to trees, graphs can contain cycles. That means, as we’ve seen in the previous section, we have to remember the nodes we visited to avoid an infinite loop. We’ll see in a moment how to update the algorithm to consider this problem, but first, let’s define our graph structure:
树的情况就这样结束了。现在让我们来看看如何处理图的情况。与树相比,图可以包含循环。这意味着,正如我们在上一节所看到的,我们必须记住我们访问过的节点,以避免无限循环。我们稍后会看到如何更新算法以考虑这个问题,但首先,让我们定义我们的图结构。
public class Node<T> {
private T value;
private Set<Node<T>> neighbors;
public Node(T value) {
this.value = value;
this.neighbors = new HashSet<>();
}
public void connect(Node<T> node) {
if (this == node) throw new IllegalArgumentException("Can't connect node to itself");
this.neighbors.add(node);
node.neighbors.add(this);
}
}Now, we can see that, in opposition to trees, we can freely connect a node with another one, giving us the possibility to create cycles. The only exception is that a node can’t connect to itself.
现在,我们可以看到,与树相反,我们可以自由地将一个节点与另一个节点连接起来,使我们有可能创建循环。唯一的例外是,一个节点不能连接到它自己。
It’s also worth noting that with this representation, there is no root node. This is not a problem, as we also made the connections between nodes bidirectional. That means we’ll be able to search through the graph starting at any node.
还值得注意的是,在这种表现形式下,没有根节点。这不是一个问题,因为我们也使节点之间的连接是双向的。这意味着我们将能够从任何节点开始在图中进行搜索。
First of all, let’s reuse the algorithm from above, adapted to the new structure:
首先,让我们重新使用上面的算法,适应新的结构。
public static <T> Optional<Node<T>> search(T value, Node<T> start) {
Queue<Node<T>> queue = new ArrayDeque<>();
queue.add(start);
Node<T> currentNode;
while (!queue.isEmpty()) {
currentNode = queue.remove();
if (currentNode.getValue().equals(value)) {
return Optional.of(currentNode);
} else {
queue.addAll(currentNode.getNeighbors());
}
}
return Optional.empty();
}We can’t run the algorithm like this, or any cycle will make it run forever. So, we must add instructions to take care of the already visited nodes:
我们不能像这样运行算法,否则任何一个循环都会使它永远运行下去。因此,我们必须添加指令来处理已经访问过的节点。
while (!queue.isEmpty()) {
currentNode = queue.remove();
LOGGER.debug("Visited node with value: {}", currentNode.getValue());
if (currentNode.getValue().equals(value)) {
return Optional.of(currentNode);
} else {
alreadyVisited.add(currentNode);
queue.addAll(currentNode.getNeighbors());
queue.removeAll(alreadyVisited);
}
}
return Optional.empty();As we can see, we first initialize a Set that’ll contain the visited nodes.
正如我们所看到的,我们首先初始化一个Set,它将包含被访问的节点。
Set<Node<T>> alreadyVisited = new HashSet<>();Then, when the comparison of values fails, we add the node to the visited ones:
然后,当数值比较失败时,我们将该节点添加到访问的节点中。
alreadyVisited.add(currentNode);Finally, after adding the node’s neighbors to the queue, we remove from it the already visited nodes (which is an alternative way of checking the current node’s presence in that set):
最后,在将节点的邻居加入队列后,我们从队列中删除已经访问过的节点(这是检查当前节点在该集合中存在的另一种方法)。
queue.removeAll(alreadyVisited);By doing this, we make sure that the algorithm won’t fall into an infinite loop.
通过这样做,我们确保算法不会陷入无限循环。。
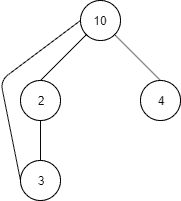
Let’s see how it works through an example. First of all, we’ll define a graph, with a cycle:
让我们通过一个例子看看它是如何工作的。首先,我们将定义一个图形,有一个周期。
And the same in Java code:
而在Java代码中也是如此。
Node<Integer> start = new Node<>(10);
Node<Integer> firstNeighbor = new Node<>(2);
start.connect(firstNeighbor);
Node<Integer> firstNeighborNeighbor = new Node<>(3);
firstNeighbor.connect(firstNeighborNeighbor);
firstNeighborNeighbor.connect(start);
Node<Integer> secondNeighbor = new Node<>(4);
start.connect(secondNeighbor);Let’s again say we want to search for the value 4. As there is no root node, we can begin the search with any node we want, and we’ll choose firstNeighborNeighbor:
让我们再次假设我们要搜索的是数值4。由于没有根节点,我们可以从任何我们想要的节点开始搜索,我们将选择firstNeighborNeighbor。
BreadthFirstSearchAlgorithm.search(4, firstNeighborNeighbor);Again, we’ll add a log to see which nodes are visited, and we expect them to be 3, 2, 10 and 4, only once each in that order:
同样,我们将添加一个日志,看看哪些节点被访问,我们希望它们是3、2、10和4,按照这个顺序每个节点只访问一次。
[main] DEBUG c.b.a.b.BreadthFirstSearchAlgorithm - Visited node with value: 3
[main] DEBUG c.b.a.b.BreadthFirstSearchAlgorithm - Visited node with value: 2
[main] DEBUG c.b.a.b.BreadthFirstSearchAlgorithm - Visited node with value: 10
[main] DEBUG c.b.a.b.BreadthFirstSearchAlgorithm - Visited node with value: 43.3. Complexity
3.3.复杂性
Now that we’ve covered both algorithms in Java, let’s talk about their time complexity. We’ll use the Big-O notation to express them.
现在我们已经涵盖了Java中的两种算法,让我们来谈谈它们的时间复杂性。我们将使用Big-O notation来表达它们。
Let’s start with the tree algorithm. It adds a node to the queue at most once, therefore visiting it at most once also. Thus, if n is the number of nodes in the tree, the time complexity of the algorithm will be O(n).
让我们从树形算法开始。它在队列中最多添加一次节点,因此也最多访问一次。因此,如果n是树上的节点数,算法的时间复杂度将是O(n)。
Now, for the graph algorithm, things are a little bit more complicated. We’ll go through each node at most once, but to do so we’ll make use of operations having linear-complexity such as addAll() and removeAll().
现在,对于图的算法来说,事情就有点复杂了。我们将对每个节点最多浏览一次,但为此我们将利用具有线性复杂性的操作,如addAll()和removeAll()。
Let’s consider n the number of nodes and c the number of connections of the graph. Then, in the worst case (being no node found), we might use addAll() and removeAll() methods to add and remove nodes up to the number of connections, giving us O(c) complexity for these operations. So, provided that c > n, the complexity of the overall algorithm will be O(c). Otherwise, it’ll be O(n). This is generally noted O(n + c), which can be interpreted as a complexity depending on the greatest number between n and c.
让我们考虑n节点的数量和c图的连接数量。然后,在最坏的情况下(没有找到节点),我们可以使用addAll()和removeAll()方法来添加和删除节点,直到连接数,给我们提供O(c)这些操作的复杂性。因此,只要c > n,整个算法的复杂性将是O(c)。否则,它将是O(n)。这一般是注意到的O(n + c)/a>,它可以被解释为取决于n和c之间最大数字的复杂性。
Why didn’t we have this problem for the tree search? Because the number of connections in a tree is bounded by the number of nodes. The number of connections in a tree of n nodes is n – 1.
为什么我们在树形搜索中没有这个问题?因为树中的连接数是由节点数来限制的。一棵有n个节点的树的连接数是n – 1。
4. Conclusion
4.总结
In this article, we learned about the Breadth-First Search algorithm and how to implement it in Java.
在这篇文章中,我们了解了广度优先搜索算法以及如何在Java中实现它。
After going through a bit of theory, we saw Java implementations of the algorithm and discussed its complexity.
在经历了一些理论之后,我们看到了该算法的Java实现,并讨论了其复杂性。
As usual, the code is available over on GitHub.
像往常一样,代码可以在GitHub上找到。