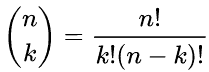1. Overview
1.概述
In this tutorial, we’ll learn how to solve a few common combinatorial problems. They are most likely not very useful in an everyday job; however, they’re interesting from the algorithmic perspective. We may find them handy for testing purposes.
在本教程中,我们将学习如何解决一些常见的组合问题。它们在日常工作中很可能并不十分有用;然而,从算法的角度来看,它们很有趣。我们可能会发现它们在测试方面很方便。。
Keep in mind that there are many different approaches to solve these problems. We’ve tried to make the solutions presented easy to grasp.
请记住,有许多不同的方法来解决这些问题。我们已经努力使提出的解决方案易于掌握。
2. Generating Permutations
2.生成排列组合
First, let’s start with permutations. A permutation is an act of rearranging a sequence in such a way that it has a different order.
首先,让我们从排列组合开始。变化是将一个序列重新排列,使其具有不同的顺序的行为。
As we know from math, for a sequence of n elements, there are n! different permutations. n! is known as a factorial operation:
正如我们从数学中知道的,对于一个n元素的序列,有n!不同的排列组合。n!被称为factorial操作。
n! = 1 * 2 * … * n
n!= 1 * 2 * … * n
So, for example, for a sequence [1, 2, 3] there are six permutations:
因此,例如,对于一个序列[1,2,3],有六种排列组合。
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]Factorial grows very fast — for a sequence of 10 elements, we have 3,628,800 different permutations! In this case, we talk about permuting sequences, where every single element is different.
因式的增长速度非常快–对于一个有10个元素的序列,我们有3,628,800种不同的排列组合!在这种情况下,我们谈论的是排列组合,其中每个元素都是不同的。
2.1. Algorithm
2.1.算法
It’s a good idea to think about generating permutations in a recursive manner. Let’s introduce the idea of the state. It will consist of two things: the current permutation and the index of the currently processed element.
以递归的方式考虑生成 permutations 是一个好主意。让我们介绍一下状态的概念。它将由两件事组成:当前的排列组合和当前处理的元素的索引。
The only work to do in such a state is to swap the element with every remaining one and perform a transition to a state with the modified sequence and the index increased by one.
在这样的状态下,唯一要做的工作是将该元素与剩余的每一个元素进行交换,并执行过渡到一个具有修改后的序列和索引增加1的状态。
Let’s illustrate with an example.
让我们用一个例子来说明。
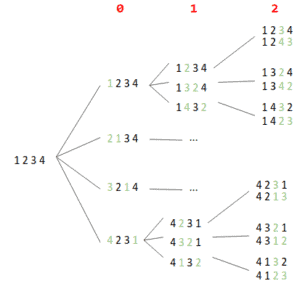
We want to generate all permutations for a sequence of four elements – [1, 2, 3, 4]. So, there will be 24 permutations. The illustration below presents the partial steps of the algorithm:
我们想为一个由四个元素组成的序列生成所有的排列组合–[1, 2, 3, 4]。因此,将有24种排列组合。下面的图示展示了算法的部分步骤。
Each node of the tree can be understood as a state. The red digits across the top indicate the index of the currently processed element. The green digits in the nodes illustrate swaps.
树的每个节点都可以理解为一个状态。横跨顶部的红色数字表示当前处理的元素的索引。节点中的绿色数字说明了交换的情况。
So, we start in the state [1, 2, 3, 4] with an index equal to zero. We swap the first element with each element – including the first, which swaps nothing – and move on to the next state.
所以,我们从索引等于0的状态[1, 2, 3, 4]开始。我们将第一个元素与每个元素互换–包括第一个元素,它没有互换–然后进入下一个状态。
Now, our desired permutations are located in the last column on the right.
现在,我们想要的排列组合位于右边的最后一列。
2.2. Java Implementation
2.2.Java实现
The algorithm written in Java is short:
用Java编写的算法很短。
private static void permutationsInternal(List<Integer> sequence, List<List<Integer>> results, int index) {
if (index == sequence.size() - 1) {
permutations.add(new ArrayList<>(sequence));
}
for (int i = index; i < sequence.size(); i++) {
swap(sequence, i, index);
permutationsInternal(sequence, permutations, index + 1);
swap(sequence, i, index);
}
}Our function takes three parameters: the currently processed sequence, results (permutations), and the index of the element currently being processed.
我们的函数需要三个参数:当前处理的序列、结果(permutations)和当前处理的元素的索引。
The first thing to do is to check if we’ve reached the last element. If so, we add the sequence to the results list.
要做的第一件事是检查我们是否已经到达了最后一个元素。如果是,我们就把这个序列添加到结果列表中。
Then, in the for-loop, we perform a swap, do a recursive call to the method, and then swap the element back.
然后,在for-loop中,我们进行交换,对方法进行递归调用,然后再把元素换回来。
The last part is a little performance trick – we can operate on the same sequence object all the time without having to create a new sequence for every recursive call.
最后一部分是一个小的性能技巧–我们可以一直对同一个序列对象进行操作,而不必为每个递归调用创建一个新的序列。
It might also be a good idea to hide the first recursive call under a facade method:
把第一个递归调用隐藏在一个facade方法下可能也是一个好主意。
public static List<List<Integer>> generatePermutations(List<Integer> sequence) {
List<List<Integer>> permutations = new ArrayList<>();
permutationsInternal(sequence, permutations, 0);
return permutations;
}
Keep in mind that the algorithm shown will work only for sequences of unique elements! Applying the same algorithm for sequences with recurring elements will give us repetitions.
请记住,所显示的算法只对独特元素的序列有效!对具有重复元素的序列应用相同的算法,将得到重复的结果。对具有重复元素的序列应用同样的算法,我们将得到重复的结果。
3. Generating the Powerset of a Set
3.生成一个集合的幂集
Another popular problem is generating the powerset of a set. Let’s start with the definition:
另一个流行的问题是生成一个集合的幂集。让我们从定义开始。
powerset (or power set) of set S is the set of all subsets of S including the empty set and S itself
集合S的幂集(或幂集)是S的所有子集的集合,包括空集和S本身。
So, for example, given a set [a, b, c], the powerset contains eight subsets:
因此,例如,给定一个集合[a, b, c],poweret包含八个子集。
[]
[a]
[b]
[c]
[a, b]
[a, c]
[b, c]
[a, b, c]We know from math that, for a set containing n elements, the powerset should contain 2^n subsets. This number also grows rapidly, however not as fast as factorial.
我们从数学上知道,对于一个包含n元素的集合,幂集应该包含2^n子集。这个数字也会迅速增长,然而没有阶乘那么快。
3.1. Algorithm
3.1.算法
This time, we’ll also think recursively. Now, our state will consist of two things: the index of the element currently being processed in a set and an accumulator.
这一次,我们也会递归地思考。现在,我们的状态将由两样东西组成:当前正在处理的元素在集合中的索引和一个累积器。
We need to make a decision with two choices in each state: whether or not to put the current element in the accumulator. When our index reaches the end of the set, we have one possible subset. In such a way, we can generate every possible subset.
我们需要做一个决定,在每个状态下有两个选择:是否将当前元素放入累加器中。当我们的索引到达集合的末端时,我们有一个可能的子集。以这样的方式,我们可以生成每一个可能的子集。
3.2. Java Implementation
3.2.Java实现
Our algorithm written in Java is pretty readable:
我们用Java编写的算法是相当可读的。
private static void powersetInternal(
List<Character> set, List<List<Character>> powerset, List<Character> accumulator, int index) {
if (index == set.size()) {
results.add(new ArrayList<>(accumulator));
} else {
accumulator.add(set.get(index));
powerSetInternal(set, powerset, accumulator, index + 1);
accumulator.remove(accumulator.size() - 1);
powerSetInternal(set, powerset, accumulator, index + 1);
}
}Our function takes four parameters: a set for which we want to generate subsets, the resulting powerset, the accumulator, and the index of the currently processed element.
我们的函数需要四个参数:一个我们想要产生子集的集合,产生的幂集,累加器,以及当前处理的元素的索引。
For simplicity, we keep our sets in lists. We want to have fast access to elements specified by index, which we can achieve it with List, but not with Set.
为了简单起见,我们把我们的集合放在列表中。我们希望能够快速访问由索引指定的元素,这一点我们可以通过List实现,但不能通过Set。
Additionally, a single element is represented by a single letter (Character class in Java).
此外,单个元素由一个字母表示(Java中的Character class)。
First, we check if the index exceeds the set size. If it does, then we put the accumulator into the result set, otherwise we:
首先,我们检查索引是否超过了集合的大小。如果是,那么我们将累加器放入结果集,否则我们。
- put the currently considered element into the accumulator
- make a recursive call with incremented index and extended accumulator
- remove the last element from the accumulator, which we added previously
- do a call again with unchanged accumulator and the incremented index
Again, we hide the implementation with a facade method:
同样,我们用一个facade方法来隐藏这个实现。
public static List<List<Character>> generatePowerset(List<Character> sequence) {
List<List<Character>> powerset = new ArrayList<>();
powerSetInternal(sequence, powerset, new ArrayList<>(), 0);
return powerset;
}4. Generating Combinations
4.产生组合
Now, it’s time to tackle combinations. We define it as follows:
现在,是时候解决组合的问题了。我们将其定义如下。
k-combination of a set S is a subset of k distinct elements from S, where an order of items doesn’t matter
k组合的集合S是k来自S的不同元素的一个子集,其中项目的顺序并不重要。
The number of k-combinations is described by the binomial coefficient:
k-combinations的数量由二项式系数描述。
So, for example, for the set [a, b, c] we have three 2-combinations:
因此,例如,对于集合[a, b, c] 我们有三个2组合。
[a, b]
[a, c]
[b, c]Combinations have many combinatorial usages and explanations. As an example, let’s say we have a football league consisting of 16 teams. How many different matches can we see?
组合有许多组合的用法和解释。作为一个例子,假设我们有一个由16支球队组成的足球联赛。我们可以看到多少场不同的比赛?
The answer is ![]() , which evaluates to 120.
, which evaluates to 120.
答案是![]() ,评估结果为120。
,评估结果为120。
4.1. Algorithm
4.1.算法
Conceptually, we’ll do something similar to the previous algorithm for powersets. We’ll have a recursive function, with state consisting of the index of the currently processed element and an accumulator.
从概念上讲,我们将做一些类似于先前的幂集算法的事情。我们将有一个递归函数,其状态由当前处理的元素的索引和一个累积器组成。
Again, we’ve got the same decision for each state: Do we add the element to the accumulator? This time, though, we have an additional restriction – our accumulator can’t have more than k elements.
同样,我们对每个状态都有相同的决定。 这一次,我们有一个额外的限制–我们的累积器不能有超过k的元素.。
It’s worth noticing that the binomial coefficient doesn’t necessarily need to be a huge number. For example:
值得注意的是,二项式系数不一定需要是一个巨大的数字。比如说。
4.2. Java Implementation
4.2.Java实现
For simplicity, we assume that elements in our set are integers.
为了简单起见,我们假设我们集合中的元素是整数。
Let’s take a look at the Java implementation of the algorithm:
让我们来看看该算法的Java实现。
private static void combinationsInternal(
List<Integer> inputSet, int k, List<List<Integer>> results, ArrayList<Integer> accumulator, int index) {
int needToAccumulate = k - accumulator.size();
int canAcculumate = inputSet.size() - index;
if (accumulator.size() == k) {
results.add(new ArrayList<>(accumulator));
} else if (needToAccumulate <= canAcculumate) {
combinationsInternal(inputSet, k, results, accumulator, index + 1);
accumulator.add(inputSet.get(index));
combinationsInternal(inputSet, k, results, accumulator, index + 1);
accumulator.remove(accumulator.size() - 1);
}
}This time, our function has five parameters: an input set, k parameter, a result list, an accumulator, and the index of the currently processed element.
这一次,我们的函数有五个参数:一个输入集,k 参数,一个结果列表,一个累加器,以及当前处理元素的索引。
We start by defining helper variables:
我们从定义辅助变量开始。
- needToAccumulate – indicates how many more elements we need to add to our accumulator to get a proper combination
- canAcculumate – indicates how many more elements we can add to our accumulator
Now, we check if our accumulator size is equal to k. If so, then we can put the copied array into the results list.
现在,我们检查我们的累积器大小是否等于k。如果是,那么我们就可以把复制的数组放到结果列表中。
In another case, if we still have enough elements in the remaining part of the set, we make two separate recursive calls: with and without the currently processed element being put into the accumulator. This part is analogous to how we generated the powerset earlier.
在另一种情况下,如果我们在集合的剩余部分仍有足够的元素,我们会进行两次单独的递归调用:有和没有当前处理的元素被放入累加器。这部分类似于我们之前生成权力集合的方式。
Of course, this method could’ve been written to work a little bit faster. For example, we could declare needToAccumulate and canAcculumate variables later. However, we are focused on readability.
当然,这个方法本来可以写得更快一点。例如,我们可以稍后声明needToAccumulate和canAcculumate变量。然而,我们的重点是可读性。
Again, a facade method hides the implementation:
同样,一个门面方法隐藏了实现。
public static List<List<Integer>> combinations(List<Integer> inputSet, int k) {
List<List<Integer>> results = new ArrayList<>();
combinationsInternal(inputSet, k, results, new ArrayList<>(), 0);
return results;
}5. Summary
5.摘要
In this article, we’ve discussed different combinatorial problems. Additionally, we’ve shown simple algorithms to solve them with implementations in Java. In some cases, these algorithms can help with unusual testing needs.
在这篇文章中,我们已经讨论了不同的组合问题。此外,我们还展示了用Java实现的简单算法来解决它们。在某些情况下,这些算法可以帮助满足不寻常的测试需求。
As usual, the complete source code, with tests, is available over on GitHub.
像往常一样,完整的源代码,包括测试,可在GitHub上获得over。