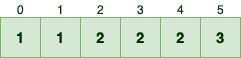Counting Sort in Java – Java中的计数排序

最后修改: 2019年 9月 1日

中文/混合/英文(键盘快捷键：t)

1. Overview

1.概述

General-purpose sorting algorithms like Merge Sort make no assumption about the input, so they can’t beat the O(n log n) in the worst case. Counting Sort, on the contrary, has an assumption about the input which makes it a linear time sorting algorithm.

像Merge Sort这样的通用排序算法没有对输入进行假设，所以它们在最坏的情况下无法战胜O(n log n)。相反，计数排序有一个关于输入的假设，这使得它成为一个线性时间排序算法。

In this tutorial, we’re going to get acquainted with the mechanics of the Counting Sort and then implement it in Java.

在本教程中，我们将熟悉计数排序的机械原理，然后用Java实现它。

2. Counting Sort

2.计数排序

Counting sort, as opposed to most classic sorting algorithms, does not sort the given input by comparing the elements. Instead, it assumes that the input elements are n integers in the range [0, k]. When k = O(n), then the counting sort will run in O(n) time.

与大多数经典的排序算法不同，计数排序并不是通过比较元素来对给定的输入进行排序。相反，它假设输入的元素是n范围[0, k]的整数。当k=O(n)时，那么计数排序将以O(n)时间运行。

Please note, then, that we can’t use the counting sort as a general-purpose sorting algorithm. However, when the input is aligned with this assumption, it’s pretty fast!

那么，请注意，我们不能把计数排序作为一种通用的排序算法。然而，当输入与这个假设相一致时，它的速度是相当快的!

2.1. Frequency Array

2.1.频率阵列

Let’s suppose we’re going to sort an input array with values in the [0, 5] range:

假设我们要对一个输入数组进行排序 ，其值在[0, 5]范围内：

To Sort Array

First, we should count the occurrence of each number in the input array. If we represent the countings with array C, then C[i] represents the frequency of number i in the input array:

首先，我们应该计算输入数组中每个数字的出现次数。如果我们用数组C表示计数，那么C[i] 代表数字i在输入数组中的频率。

counts

For example, since 5 appears 3 times in the input array, the value for the index 5 is equal to 3.

例如，由于5在输入数组中出现3次，所以索引5的值等于3。

Now given the array C, we should determine how many elements are less than or equal to each input element. For example:

现在给定数组C,我们应该确定有多少元素小于或等于每个输入元素。例如。

  • One element is less than or equal to zero, or in other words, there is only one zero value, which is equal to C[0]
  • Two elements are less than or equal to one, which is equal to C[0] + C[1]
  • Four values are less than or equal to two, which is equal to C[0] + C[1] + C[2]

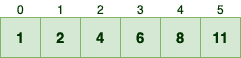
So if we keep computing the summation of n consecutive elements in C, we can know how many elements are less than or equal to number n-1 in the input array. Anyway, by applying this simple formula we can update the C as the following:

因此，如果我们不断计算C中n个连续元素的和，我们就可以知道在输入数组中，有多少元素小于或等于n-1号。无论如何，通过应用这个简单的公式，我们可以更新C如下。

less than

2.2. The Algorithm

2.2.算法

Now we can use the auxiliary array C to sort the input array. Here’s how the counting sort works:

现在我们可以使用辅助数组C来对输入数组进行排序。下面是计数排序的工作原理。

  • It iterates the input array in reverse
  • For each element i, C[i] – 1 represents the location of number i in the sorted array. This is because of the fact that there are C[i] elements less than or equal to i
  • Then, it decrements the C[i] at the end of each round

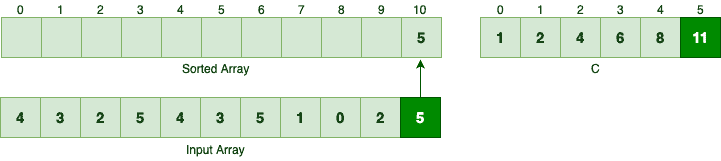
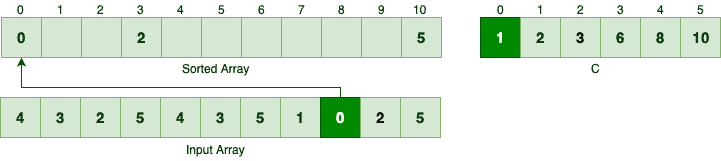
In order to sort the sample input array, we should first start with the number 5, since it’s the last element. According to C[5], there are 11 elements are less than or equal to the number 5.

为了对样本输入数组进行排序，我们首先应该从数字5开始，因为它是最后一个元素。根据C[5]，有11个元素小于或等于数字5。

So, 5 should be the 11th element in the sorted array, hence the index 10:

所以，5应该是排序后的数组中的第11个元素，因此索引为10。

Untitled Diagram

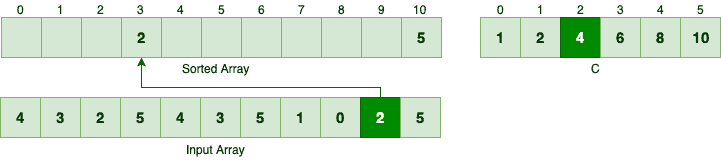
Since we moved 5 to the sorted array, we should decrement the C[5]. Next element in the reversed order is 2. Since there are 4 elements less than or equal to 2, this number should be the 4th element in the sorted array:

因为我们把5移到了排序的数组中，所以我们应该减去C[5]。下一个颠倒顺序的元素是2，由于有4个元素小于或等于2，这个数字应该是排序数组中的第4个元素。

Untitled Diagram 1

Similarly, we can find the right spot for the next element which is 0:

同样地，我们可以为下一个元素找到合适的位置，这个元素就是0。

Untitled Diagram 2

If we keep iterating in reverse and move each element appropriately, we would end up with something like:

如果我们继续反向迭代，并适当地移动每个元素，我们最终会得到这样的结果。

Untitled Diagram 3

3. Counting Sort – Java Implementation

3.计数排序–Java实现

3.1. Computing the Frequency Array

3.1.计算频率阵列

First off, given an input array of elements and the k, we should compute the array C:

首先，给定一个输入的元素数组和k，我们应该计算数组C:。

int[] countElements(int[] input, int k) {
    int[] c = new int[k + 1];
    Arrays.fill(c, 0);

    for (int i : input) {
        c[i] += 1;
    }

    for (int i = 1; i < c.length; i++) {
	c[i] += c[i - 1];
    }

    return c;
}

Let’s breakdown the method signature:

让我们来分析一下这个方法的签名。

  • input represents an array of numbers we’re going to sort
  • The input array is an array of integers in the range of [0, k] – so k represents the maximum number in the input
  • The return type is an array of integers representing the C array

And here’s how the countElements method works:

这里是countElements方法的工作原理。

  • First, we initialized the C array. As the [0, k] range contains k+1 numbers, we’re creating an array capable of containing k+1 numbers
  • Then for each number in the input, we’re computing the frequency of that number
  • And finally, we’re adding consecutive elements together to know how many elements are less than or equal to a particular number

Also, we can verify that the countElements method works as expected:

另外，我们可以验证countElements方法是否如预期的那样工作。

@Test
void countElements_GivenAnArray_ShouldCalculateTheFrequencyArrayAsExpected() {
    int k = 5;
    int[] input = { 4, 3, 2, 5, 4, 3, 5, 1, 0, 2, 5 };
    
    int[] c = CountingSort.countElements(input, k);
    int[] expected = { 1, 2, 4, 6, 8, 11 };
    assertArrayEquals(expected, c);
}

3.2. Sorting the Input Array

3.2.对输入数组进行排序

Now that we can calculate the frequency array, we should be able to sort any given set of numbers:

现在我们可以计算频率数组了，我们应该可以对任何给定的数字集进行排序。

int[] sort(int[] input, int k) {
    int[] c = countElements(input, k);

    int[] sorted = new int[input.length];
    for (int i = input.length - 1; i >= 0; i--) {
        int current = input[i];
	sorted[c[current] - 1] = current;
	c[current] -= 1;
    }

    return sorted;
}

Here’s how the sort method works:

下面是sort方法的工作原理。

  • First, it computes the C array
  • Then, it iterates the input array in reverse and for each element in the input, finds its correct spot in the sorted array. The ith element in the input should be the C[i]th element in the sorted array. Since Java arrays are zero-indexed, the C[i]-1 entry is the C[i]th element – for example, sorted[5] is the sixth element in the sorted array
  • Each time we find a match, it decrements the corresponding C[i] value

Similarly, we can verify that the sort method works as expected:

同样地，我们可以验证sort 方法是否如预期那样工作。

@Test
void sort_GivenAnArray_ShouldSortTheInputAsExpected() {
    int k = 5;
    int[] input = { 4, 3, 2, 5, 4, 3, 5, 1, 0, 2, 5 };

    int[] sorted = CountingSort.sort(input, k);

    // Our sorting algorithm and Java's should return the same result
    Arrays.sort(input);
    assertArrayEquals(input, sorted);
}

4. Revisiting the Counting Sort Algorithm

4.重新审视计数排序算法

4.1. Complexity Analysis

4.1.复杂度分析

Most classic sorting algorithms, like merge sort, sort any given input by just comparing the input elements to each other. These type of sorting algorithms are known as comparison sorts. In the worst case, comparison sorts should take at least O(n log n) to sort n elements.

大多数经典的排序算法，如merge sort，仅通过将输入元素相互比较来对任何给定输入进行排序。这些类型的排序算法被称为比较排序。在最坏的情况下，比较排序应该至少需要O(n log n)来对n元素进行排序。

Counting Sort, on the other hand, does not sort the input by comparing the input elements, so it’s clearly not a comparison sort algorithm.

另一方面，计数排序并不是通过比较输入元素来排序的，所以它显然不是一种比较排序算法。

Let’s see how much time it consumes to sort the input:

让我们看看对输入进行排序需要消耗多少时间。

  • It computes the C array in O(n+k) time: It once iterates an input array with size n in O(n) and then iterates the C in O(k) – so that would be O(n+k) in total
  • After computing the C, it sorts the input by iterating the input array and performing a few primitive operations in each iteration. So, the actual sort operation takes O(n)

In total, counting sort takes O(n+k) time to run:

总的来说，计数排序需要O(n+k) 时间来运行。

O(n + k) + O(n) = O(2n + k) = O(n + k)

If we assume k=O(n), then counting sort algorithm sorts the input in linear time. As opposed to general-purpose sorting algorithms, counting sorts makes an assumption about the input and takes less than the O(n log n) lower bound to execute.

如果我们假设k=O(n)，那么计数排序算法会在线性时间内对输入进行排序。与通用排序算法相比，计数排序对输入进行了假设，并且执行的时间小于O(n log n) 下限。

 4.2. Stability

4.2.稳定性

A few moments ago, we laid a few peculiar rules about the mechanics of counting sort but never cleared the reason behind them. To be more specific:

刚才，我们对计数排序的机制制定了一些奇特的规则，但从未清除其背后的原因。说得更具体一点。

  • Why should we iterate the input array in reverse?
  • Why we decrement the C[i] each time we’re using it?

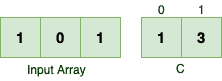
Let’s iterate from the beginning to better understand the first rule. Suppose we’re going to sort a simple array of integers like the following:

让我们从头开始迭代，以便更好地理解第一条规则。假设我们要对一个简单的整数数组进行排序，如下所示。

Untitled Diagram 4

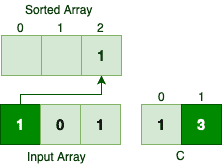
In the first iteration, we should find the sorted location for the first 1:

在第一次迭代中，我们应该为第一个1找到排序的位置。

Untitled Diagram 5

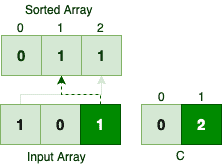
So the first occurrence of number 1 gets the last index in the sorted array. Skipping the number 0, let’s see what happens to the second occurrence of number 1:

所以第一次出现的数字1在排序的数组中得到了最后的索引。跳过数字0，让我们看看数字1的第二次出现会怎样。

Untitled Diagram 6

The appearance order of elements with the same value is different in the input and sorted array, so the algorithm is not stable when we’re iterating from the beginning.

在输入数组和排序数组中，具有相同值的元素的外观顺序是不同的，所以当我们从头开始迭代时，该算法不是稳定的。。

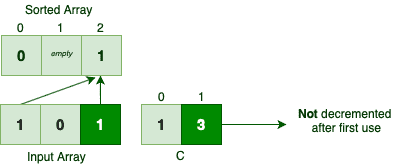
What happens if we don’t decrement the C[i] value after each use? Let’s see:

如果我们不在每次使用后递减C[i]值，会发生什么？让我们来看看。

Untitled Diagram 2 1

Both occurrences of number 1 are getting the last place in the sorted array. So if we don’t decrement the C[i] value after each use, we could potentially lose a few numbers while sorting them!

数字1的两次出现都是在排序的数组中获得最后的位置。因此，如果我们不在每次使用后递减C[i]值，我们就有可能在排序时丢失一些数字!

5. Conclusion

5.总结

In this tutorial, first, we learned how the Counting Sort works internally. Then we implemented this sorting algorithm in Java and wrote a few tests to verify its behavior. And finally, we proved that the algorithm is a stable sorting algorithm with linear time complexity.

在本教程中，首先，我们了解了计数排序的内部工作原理。然后，我们用Java实现了这种排序算法，并写了一些测试来验证其行为。最后，我们证明了该算法是一种具有线性时间复杂度的稳定排序算法。

As usual, the sample codes are available on our GitHub project, so make sure to check it out!

像往常一样，样本代码可以在我们的GitHub项目中找到，所以一定要去看看。