1. Introduction
1.绪论
In this tutorial, we’ll learn about the Gradient Descent algorithm. We’ll implement the algorithm in Java and illustrate it step by step.
在本教程中,我们将学习梯度下降算法。我们将在Java中实现该算法,并逐步加以说明。
2. What Is Gradient Descent?
2.什么是梯度下降?
Gradient Descent is an optimization algorithm used to find a local minimum of a given function. It’s widely used within high-level machine learning algorithms to minimize loss functions.
梯度下降是一种优化算法,用于寻找一个给定函数的局部最小值。它被广泛用于高级机器学习算法中,以最小化损失函数。
Gradient is another word for slope, and descent means going down. As the name suggests, Gradient Descent goes down the slope of a function until it reaches the end.
梯度是斜率的另一个词,而下降的意思是往下走。顾名思义,梯度下降是沿着一个函数的斜率向下走,直到到达终点。
3. Properties of Gradient Descent
3.梯度下降的特性
Gradient Descent finds a local minimum, which can be different from the global minimum. The starting local point is given as a parameter to the algorithm.
梯度下降法(Gradient Descent)可以找到一个局部最小值,它可能与全局最小值不同。开始的局部点是作为算法的一个参数给出的。
It’s an iterative algorithm, and in each step, it tries to move down the slope and get closer to the local minimum.
这是一个迭代算法,在每一步中,它都试图沿着斜坡向下移动,并接近局部最小值。
In practice, the algorithm is backtracking. We’ll illustrate and implement backtracking Gradient Descent in this tutorial.
在实践中,该算法是回溯式的。我们将在本教程中说明并实现反追踪梯度下降。
4. Step-By-Step Illustration
4.循序渐进的插图
Gradient Descent needs a function and a starting point as input. Let’s define and plot a function:
梯度下降法需要一个函数和一个起点作为输入。让我们来定义和绘制一个函数。
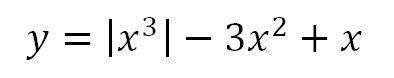
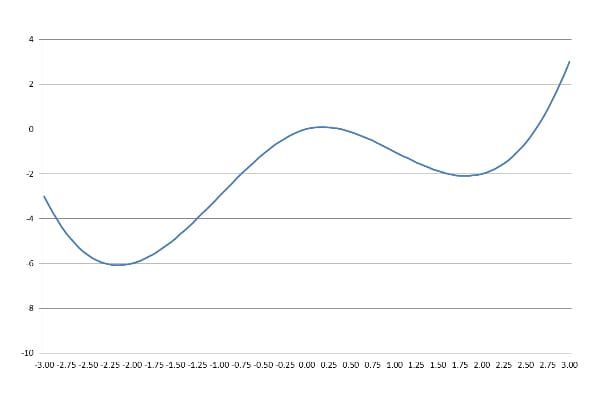
We can start at any desired point. Let’s start at x=1:
我们可以从任何想要的点开始。让我们从x=1开始。
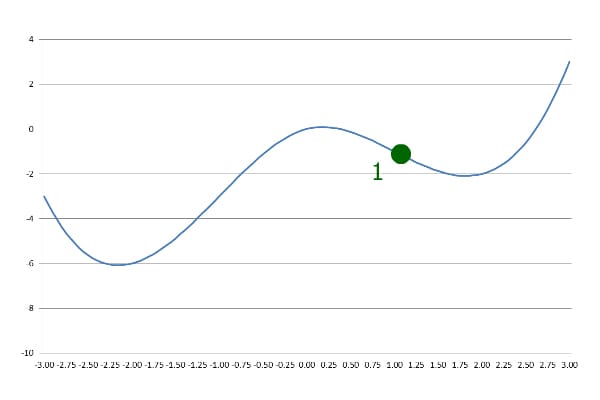
In the first step, Gradient Descent goes down the slope with a pre-defined step size:
在第一步中,梯度下降法以预先定义的步长下坡。
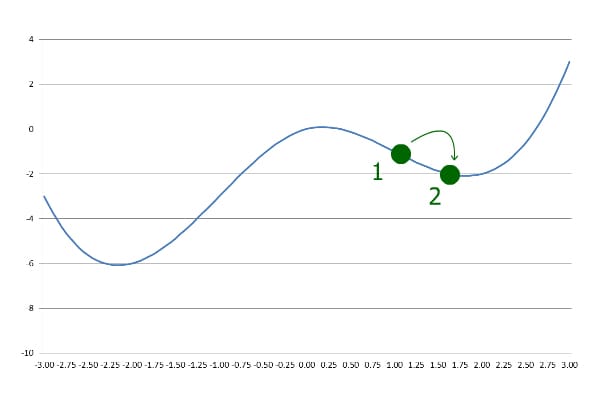
Next, it goes further with the same step size. However, this time it ends up at a greater y than the last step:
接下来,它以相同的步长继续前进。然而,这一次它的终点是比上一步更大的y。
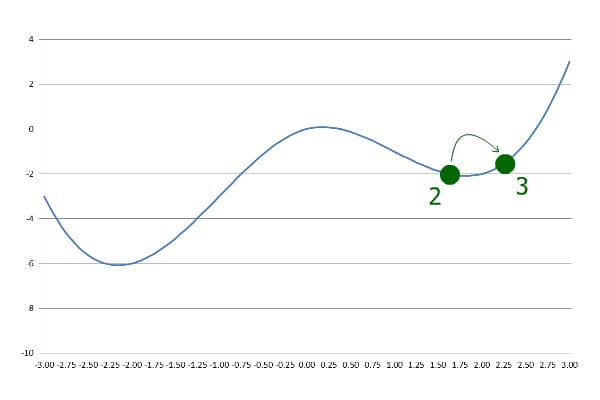
This indicates that the algorithm has passed the local minimum, so it goes backward with a lowered step size:
这表明算法已经通过了局部最小值,所以它以较小的步长向后退。
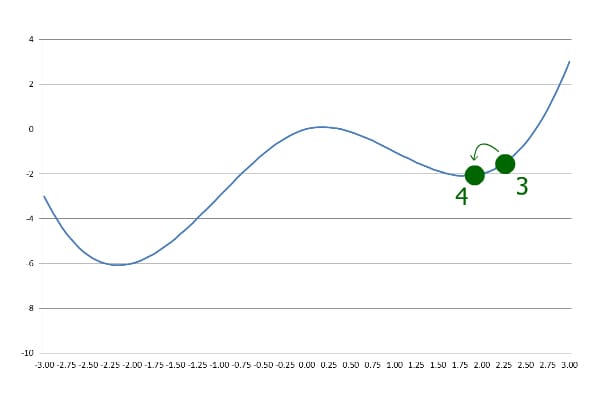
Subsequently, whenever the current y is greater than the previous y, the step size is lowered and negated. The iteration goes on until the desired precision is achieved.
随后,只要当前的y大于前一个y,步长就会降低并被否定。循环往复,直到达到理想的精度。
As we can see, Gradient Descent found a local minimum here, but it is not the global minimum. If we start at x=-1 instead of x=1, the global minimum will be found.
我们可以看到,梯度下降法在这里找到了一个局部最小值,但它不是全局最小值。如果我们从x=-1而不是x=1开始,就可以找到全局最小值。
5. Implementation in Java
5.用Java实现
There are several ways to implement Gradient Descent. Here we don’t calculate the derivative of the function to find the direction of the slope, so our implementation works for non-differentiable functions as well.
有几种方法可以实现梯度下降。这里我们不计算函数的导数来寻找斜率的方向,所以我们的实现也适用于不可微分的函数。
Let’s define precision and stepCoefficient and give them initial values:
让我们定义precision和stepCoefficient,并赋予它们初始值。
double precision = 0.000001;
double stepCoefficient = 0.1;In the first step, we don’t have a previous y for comparison. We can either increase or decrease the value of x to see if y lowers or raises. A positive stepCoefficient means we are increasing the value of x.
在第一步,我们没有之前的y进行比较。我们可以增加或减少x的值,看y是否降低或提高。一个正的stepCoefficient意味着我们正在增加x的值。
Now let’s perform the first step:
现在我们来执行第一步。
double previousX = initialX;
double previousY = f.apply(previousX);
currentX += stepCoefficient * previousY;In the above code, f is a Function<Double, Double>, and initialX is a double, both being provided as input.
在上面的代码中,f是一个Function<Double, Double>,initialX是一个double,两者都作为输入提供。
Another key point to consider is that Gradient Descent isn’t guaranteed to converge. To avoid getting stuck in the loop, let’s have a limit on the number of iterations:
另一个需要考虑的关键点是,梯度下降并不保证收敛。为了避免陷入循环,让我们对迭代的次数有一个限制。
int iter = 100;Later, we’ll decrement iter by one at each iteration. Consequently, we’ll get out of the loop at a maximum of 100 iterations.
之后,我们将在每次迭代时将iter递减1。因此,我们将在最多100次的迭代中走出循环。
Now that we have a previousX, we can set up our loop:
现在我们有一个previousX,我们可以设置我们的循环。
while (previousStep > precision && iter > 0) {
iter--;
double currentY = f.apply(currentX);
if (currentY > previousY) {
stepCoefficient = -stepCoefficient/2;
}
previousX = currentX;
currentX += stepCoefficient * previousY;
previousY = currentY;
previousStep = StrictMath.abs(currentX - previousX);
}In each iteration, we calculate the new y and compare it with the previous y. If currentY is greater than previousY, we change our direction and decrease the step size.
在每个迭代中,我们计算新的y,并与之前的y进行比较。如果currentY大于previousY,我们就改变方向,减小步长。
The loop goes on until our step size is less than the desired precision. Finally, we can return currentX as the local minimum:
这个循环一直持续到我们的步长小于所需的precision。最后,我们可以返回currentX作为局部最小值。
return currentX;6. Conclusion
6.结论
In this article, we walked through the Gradient Descent algorithm with a step-by-step illustration.
在这篇文章中,我们通过一步步的图解,走过了梯度下降算法。
We also implemented Gradient Descent in Java. The code is available over on GitHub.
我们还在Java中实现了梯度下降。该代码可在GitHub上获得。