1. Introduction
1.绪论
In this tutorial, we’re going to introduce greedy algorithms in the Java ecosystem.
在本教程中,我们将介绍Java生态系统中的贪婪算法。
2. Greedy Problem
2.贪婪问题
When facing a mathematical problem, there may be several ways to design a solution. We can implement an iterative solution, or some advanced techniques, such as divide and conquer principle (e.g. Quicksort algorithm) or approach with dynamic programming (e.g. Knapsack problem) and many more.
当面对一个数学问题时,可能有几种方法来设计一个解决方案。我们可以实现迭代解决,也可以采用一些先进的技术,如分而治之原则(如Quicksort算法)或采用动态编程的方法(如Knapsack问题)等等。
Most of the time, we’re searching for an optimal solution, but sadly, we don’t always get such an outcome. However, there are cases where even a suboptimal result is valuable. With the help of some specific strategies, or heuristics, we might earn ourselves such a precious reward.
大多数时候,我们都在寻找一个最佳解决方案,但可悲的是,我们并不总是能得到这样的结果。然而,在有些情况下,即使是一个次优的结果也是有价值的。借助一些特定的策略,或启发式方法,我们可能会为自己赢得这样宝贵的回报。
In this context, given a divisible problem, a strategy that at each stage of the process takes the locally optimal choice or “greedy choice” is called a greedy algorithm.
在这种情况下,给定一个可分割的问题,在过程的每个阶段采取局部最优选择或 “贪婪选择 “的策略被称为贪婪算法。
We stated that we should address a “divisible” problem: A situation that can be described as a set of subproblems with, almost, the same characteristics. As a consequence, most of the time, a greedy algorithm will be implemented as a recursive algorithm.
我们说过,我们应该解决一个 “可分 “的问题:一个可以被描述为一组几乎具有相同特征的子问题的情况。因此,大多数情况下,贪婪算法将作为一个递归算法来实现。
A greedy algorithm can be a way to lead us to a reasonable solution in spite of a harsh environment; lack of computational resources, execution-time constraint, API limitations, or any other kind of restrictions.
贪婪算法可以引导我们在恶劣的环境中找到合理的解决方案;缺乏计算资源,执行时间限制,API限制,或任何其他类型的限制。
2.1. Scenario
2.1. 情景
In this short tutorial, we’re going to implement a greedy strategy to extract data from a social network using its API.
在这个简短的教程中,我们将实施一个贪婪的策略,利用社交网络的API从其提取数据。
Let’s say we’d like to reach more users on the “little-blue-bird” social. The best way to achieve our goal is to post original content or re-tweet something that will arouse some interest to a broad audience.
比方说,我们想在 “小蓝鸟 “社交平台上接触更多的用户。实现我们目标的最好方法是发布原创内容或转发一些能引起广大受众兴趣的内容。
How do we find such an audience? Well, we must find an account with many followers and tweet some content for them.
我们如何找到这样的受众呢?好吧,我们必须找到一个有很多追随者的账户,并为他们推送一些内容。
2.2. Classic vs. Greedy
2.2.经典与贪婪
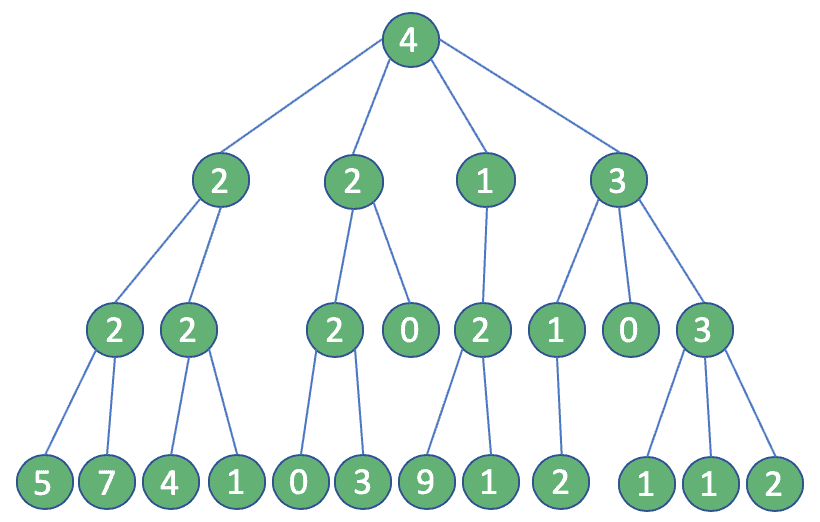
We take into account the following situation: Our account has four followers, each of which has, as depicted in the image below, respectively 2, 2, 1 and 3 followers, and so on:
我们考虑到以下情况。我们的账户有四个追随者,每个追随者都有,如下图所示,分别是2、2、1和3个追随者,以此类推。
With this purpose in our minds, we’ll take the one with more followers among the followers of our account. Then we’ll repeat the process two more times until we reach the 3rd degree of connection (four steps in total).
带着这个目的,我们将在我们账户的追随者中选择拥有更多追随者的人。然后我们再重复这个过程两次,直到我们达到第三级联系(共四个步骤)。
In this way, we define a path made of users, leading us to the vastest followers-base from our account. If we can address some content to them, they’ll surely reach our page.
通过这种方式,我们定义了一条由用户组成的路径,将我们引向我们账户中最庞大的粉丝群。如果我们能够向他们提供一些内容,他们肯定会到达我们的页面。
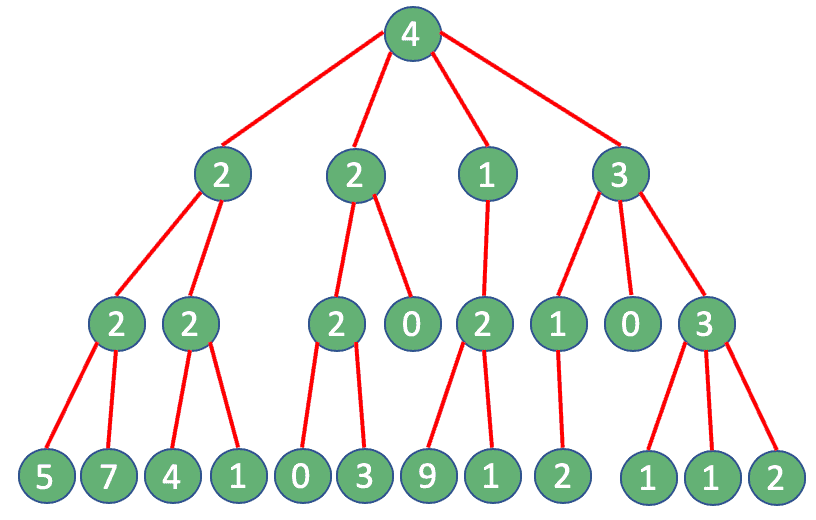
We can start with a “traditional” approach. At every single step, we’ll perform a query to get the followers of an account. As a result of our selection process, the number of accounts will increase every step.
我们可以从一个 “传统 “的方法开始。在每一个步骤中,我们都会进行查询,以获得一个账户的追随者。由于我们的选择过程,账户的数量每一步都会增加。
Surprisingly, in total, we would end up performing 25 queries:
令人惊讶的是,我们最终总共会进行25次查询。
Here a problem arises: For example, Twitter API limits this type of query to 15 every 15 minutes. If we try to perform more calls than allowed, we’ll get a “Rate limit exceeded code – 88“, or “Returned in API v1.1 when a request cannot be served due to the application’s rate limit having been exhausted for the resource“. How can we overcome such a limit?
这里出现了一个问题。例如,Twitter API将这种类型的查询限制在每15分钟15次。如果我们试图执行超过允许的调用,我们会得到一个”超过速率限制的代码 – 88“,或者”在API v1.1中返回,由于应用程序的速率限制已经用完,无法提供请求“。我们怎样才能克服这样的限制呢?
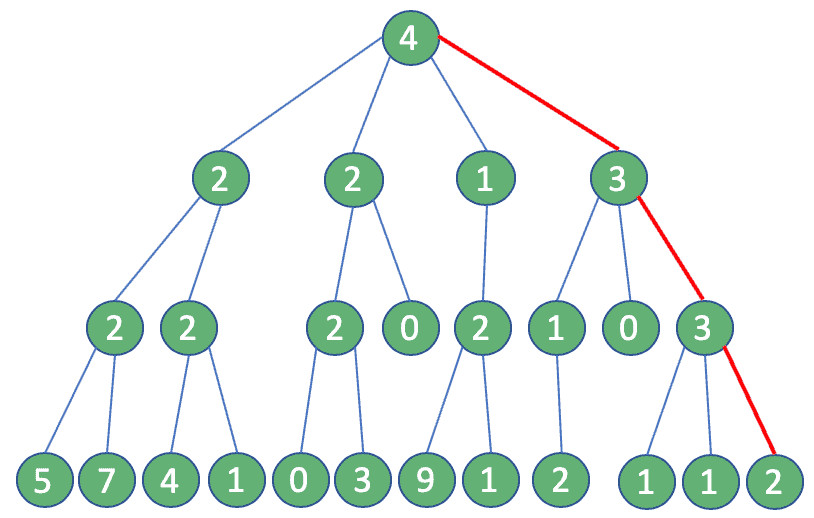
Well, the answer is right in front of us: A greedy algorithm. If we use this approach, at each step, we can assume that the user with the most followers is the only one to consider: In the end, we need only four queries. Quite an improvement!
嗯,答案就在我们面前。一个贪婪的算法。如果我们使用这种方法,在每一步,我们可以假设拥有最多追随者的用户是唯一需要考虑的用户。最后,我们只需要四个查询。这是一个相当大的进步。
The outcome of those two approaches will be different. In the first case, we get 16, the optimal solution, while in the latter, the maximum number of reachable followers is merely 12.
这两种方法的结果将是不同的。在第一种情况下,我们得到的是16,即最佳解决方案,而在后者,可达到的最大追随者数量仅仅是12。
Will this difference be so valuable? We’ll decide later.
这种差异会有这么大的价值吗?我们以后会决定。
3. Implementation
3.实施
To implement the above logic, we initialize a small Java program, where we’ll mimic the Twitter API. We’ll also make use of the Lombok library.
为了实现上述逻辑,我们初始化一个小的Java程序,在这里我们将模仿Twitter的API。我们还将利用Lombok库。
Now, let’s define our component SocialConnector in which we’ll implement our logic. Note that we’re going to put a counter to simulate calls restrictions, but we’ll lower it to four:
现在,让我们定义我们的组件SocialConnector,我们将在其中实现我们的逻辑。注意,我们要放一个计数器来模拟呼叫限制,但我们要把它降低到4。
public class SocialConnector {
private boolean isCounterEnabled = true;
private int counter = 4;
@Getter @Setter
List users;
public SocialConnector() {
users = new ArrayList<>();
}
public boolean switchCounter() {
this.isCounterEnabled = !this.isCounterEnabled;
return this.isCounterEnabled;
}
}
Then we’re going to add a method to retrieve the followers’ list of a specific account:
然后,我们将添加一个方法来检索特定账户的追随者名单。
public List getFollowers(String account) {
if (counter < 0) {
throw new IllegalStateException ("API limit reached");
} else {
if (this.isCounterEnabled) {
counter--;
}
for (SocialUser user : users) {
if (user.getUsername().equals(account)) {
return user.getFollowers();
}
}
}
return new ArrayList<>();
}
To support our process, we need some classes to model our user entity:
为了支持我们的进程,我们需要一些类来模拟我们的用户实体。
public class SocialUser {
@Getter
private String username;
@Getter
private List<SocialUser> followers;
@Override
public boolean equals(Object obj) {
return ((SocialUser) obj).getUsername().equals(username);
}
public SocialUser(String username) {
this.username = username;
this.followers = new ArrayList<>();
}
public SocialUser(String username, List<SocialUser> followers) {
this.username = username;
this.followers = followers;
}
public void addFollowers(List<SocialUser> followers) {
this.followers.addAll(followers);
}
}3.1. Greedy Algorithm
3.1.贪婪算法
Finally, it’s time to implement our greedy strategy, so let’s add a new component – GreedyAlgorithm – in which we’ll perform the recursion:
最后,是时候实现我们的贪婪策略了,所以让我们添加一个新的组件–GreedyAlgorithm–我们将在其中执行递归。
public class GreedyAlgorithm {
int currentLevel = 0;
final int maxLevel = 3;
SocialConnector sc;
public GreedyAlgorithm(SocialConnector sc) {
this.sc = sc;
}
}Then we need to insert a method findMostFollowersPath in which we’ll find the user with most followers, count them, and then proceed to the next step:
然后我们需要插入一个方法findMostFollowersPath,在这个方法中我们将找到拥有最多粉丝的用户,计算他们,然后进行下一步。
public long findMostFollowersPath(String account) {
long max = 0;
SocialUser toFollow = null;
List followers = sc.getFollowers(account);
for (SocialUser el : followers) {
long followersCount = el.getFollowersCount();
if (followersCount > max) {
toFollow = el;
max = followersCount;
}
}
if (currentLevel < maxLevel - 1) {
currentLevel++;
max += findMostFollowersPath(toFollow.getUsername());
}
return max;
}Remember: Here is where we perform a greedy choice. As such, every time we call this method, we’ll choose one and only one element from the list and move on: We won’t ever go back on our decisions!
请记住。这里是我们进行贪婪选择的地方。因此,每次我们调用这个方法时,我们将从列表中选择一个且仅有一个元素,然后继续前进。我们永远不会在我们的决定上走回头路!
Perfect! We are ready to go, and we can test our application. Before that, we need to remember to populate our tiny network and finally, execute the following unit test:
很完美!我们已经准备好了,我们可以测试我们的应用程序。在此之前,我们需要记住填充我们的小网络,最后,执行以下单元测试。
public void greedyAlgorithmTest() {
GreedyAlgorithm ga = new GreedyAlgorithm(prepareNetwork());
assertEquals(ga.findMostFollowersPath("root"), 5);
}3.2. Non-Greedy Algorithm
3.2.非补救性算法
Let’s create a non-greedy method, merely to check with our eyes what happens. So, we need to start with building a NonGreedyAlgorithm class:
让我们创建一个非贪婪的方法,仅仅是为了用我们的眼睛检查会发生什么。所以,我们需要先建立一个非贪婪算法类。
public class NonGreedyAlgorithm {
int currentLevel = 0;
final int maxLevel = 3;
SocialConnector tc;
public NonGreedyAlgorithm(SocialConnector tc, int level) {
this.tc = tc;
this.currentLevel = level;
}
}Let’s create an equivalent method to retrieve followers:
让我们创建一个同等的方法来检索追随者。
public long findMostFollowersPath(String account) {
List<SocialUser> followers = tc.getFollowers(account);
long total = currentLevel > 0 ? followers.size() : 0;
if (currentLevel < maxLevel ) {
currentLevel++;
long[] count = new long[followers.size()];
int i = 0;
for (SocialUser el : followers) {
NonGreedyAlgorithm sub = new NonGreedyAlgorithm(tc, currentLevel);
count[i] = sub.findMostFollowersPath(el.getUsername());
i++;
}
long max = 0;
for (; i > 0; i--) {
if (count[i-1] > max) {
max = count[i-1];
}
}
return total + max;
}
return total;
}As our class is ready, we can prepare some unit tests: One to verify the call limit exceeds and another one to check the value returned with a non-greedy strategy:
由于我们的类已经准备好了,我们可以准备一些单元测试。一个是验证调用限制是否超过,另一个是检查用非贪婪策略返回的值。
public void nongreedyAlgorithmTest() {
NonGreedyAlgorithm nga = new NonGreedyAlgorithm(prepareNetwork(), 0);
Assertions.assertThrows(IllegalStateException.class, () -> {
nga.findMostFollowersPath("root");
});
}
public void nongreedyAlgorithmUnboundedTest() {
SocialConnector sc = prepareNetwork();
sc.switchCounter();
NonGreedyAlgorithm nga = new NonGreedyAlgorithm(sc, 0);
assertEquals(nga.findMostFollowersPath("root"), 6);
}4. Results
4.结果
It’s time to review our work!
现在是审查我们工作的时候了
First, we tried out our greedy strategy, checking its effectiveness. Then we verified the situation with an exhaustive search, with and without the API limit.
首先,我们尝试了我们的贪婪策略,检查其有效性。然后,我们用详尽的搜索来验证这一情况,包括有无API限制。
Our quick greedy procedure, which makes locally optimal choices each time, returns a numeric value. On the other hand, we don’t get anything from the non-greedy algorithm, due to an environment restriction.
我们的快速贪婪程序,每次都做出局部最优的选择,返回一个数字值。另一方面,由于环境的限制,我们从非贪婪算法中没有得到任何东西。
Comparing the two methods’ output, we can understand how our greedy strategy saved us, even if the retrieved value that is not optimal. We can call it a local optimum.
比较两种方法的输出结果,我们可以理解我们的贪婪策略是如何拯救我们的,即使检索到的值不是最优的。我们可以称之为局部最优。
5. Conclusion
5.总结
In mutable and fast-changing contexts like social media, problems that require finding an optimal solution can become a dreadful chimera: Hard to reach and, at the same time, unrealistic.
在像社交媒体这样易变和快速变化的背景下,需要找到一个最佳解决方案的问题可能会成为一个可怕的幻象。难以达到,同时也是不现实的。
Overcoming limitations and optimizing API calls is quite a theme, but, as we’ve discussed, greedy strategies are effective. Choosing this kind of approach saves us much pain, returning valuable results in exchange.
克服限制和优化API调用是一个相当大的主题,但是,正如我们已经讨论过的,贪婪的策略是有效的。选择这种方法为我们节省了很多痛苦,换来了有价值的结果。
Keep in mind that not every situation is suitable: We need to evaluate our circumstances every time.
请记住,不是每一种情况都适合。我们每次都需要评估我们的情况。
As always, the example code from this tutorial is available over on GitHub.
一如既往,本教程的示例代码可在GitHub上获得。