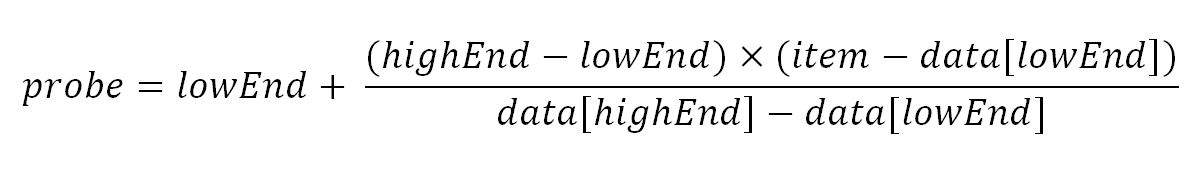1. Introduction
1.介绍
In this tutorial, we’ll walk through interpolation search algorithms and discuss their pros and cons. Furthermore, we’ll implement it in Java and talk about the algorithm’s time complexity.
在本教程中,我们将了解插值搜索算法,并讨论其优点和缺点。此外,我们将在Java中实现它,并讨论该算法的时间复杂性。
2. Motivation
2.动机
Interpolation search is an improvement over binary search tailored for uniformly distributed data.
插值搜索是对二进制搜索的改进,为均匀分布的数据量身定做。
Binary search halves the search space on each step regardless of the data distribution, thus it’s time complexity is always O(log(n)).
无论数据分布如何,二进制搜索在每一步都将搜索空间减半,因此它的时间复杂度总是O(log(n))。
On the other hand, interpolation search time complexity varies depending on the data distribution. It is faster than binary search for uniformly distributed data with the time complexity of O(log(log(n))). However, in the worst-case scenario, it can perform as poor as O(n).
另一方面,插值搜索的时间复杂度因数据分布而异。对于均匀分布的数据,它比二进制搜索快,时间复杂度为O(log(log(n))。然而,在最坏的情况下,它的表现可以差到O(n)。
3. Interpolation Search
3.插值搜索
Similar to binary search, interpolation search can only work on a sorted array. It places a probe in a calculated position on each iteration. If the probe is right on the item we are looking for, the position will be returned; otherwise, the search space will be limited to either the right or the left side of the probe.
与二进制搜索类似,插值搜索只能在一个排序的数组上工作。它在每次迭代时将探针放在一个计算好的位置上。如果探针正好在我们要找的项目上,这个位置将被返回;否则,搜索空间将被限制在探针的右边或左边。
The probe position calculation is the only difference between binary search and interpolation search.
探针位置计算是二进制搜索和插值搜索之间的唯一区别。
In binary search, the probe position is always the middlemost item of the remaining search space.
在二进制搜索中,探测位置总是剩余搜索空间的最中间一项。
In contrary, interpolation search computes the probe position based on this formula:
相反,插值搜索是根据这个公式来计算探针的位置。
Let’s take a look at each of the terms:
让我们来看看每一个术语。
- probe: the new probe position will be assigned to this parameter.
- lowEnd: the index of the leftmost item in the current search space.
- highEnd: the index of the rightmost item in the current search space.
- data[]: the array containing the original search space.
- item: the item that we are looking for.
To better understand how interpolation search works, let’s demonstrate it with an example.
为了更好地理解插值搜索的工作原理,让我们用一个例子来证明。
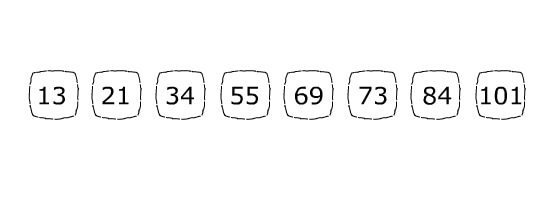
Let’s say we want to find the position of 84 in the array below:
比方说,我们想在下面的数组中找到84的位置。
The array’s length is 8, so initially highEnd = 7 and lowEnd = 0 (because array’s index starts from 0, not 1).
数组的长度是8,所以最初highEnd=7,lowEnd=0(因为数组的索引从0开始,不是1)。
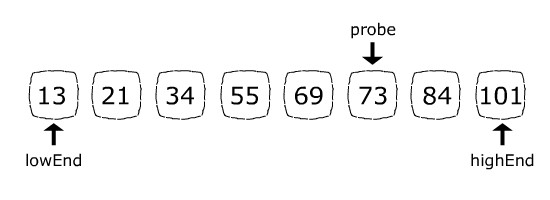
In the first step, the probe position formula will result in probe = 5:
在第一步,探针位置公式将导致probe=5。
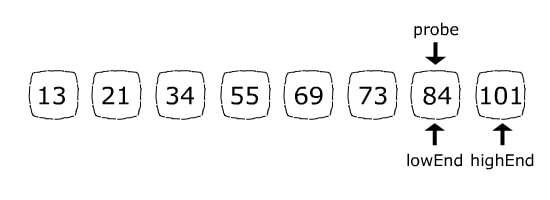
Because 84 (the item we are looking for) is greater than 73 (the current probe position item), the next step will abandon the left side of the array by assigning lowEnd = probe + 1. Now the search space consists of only 84 and 101. The probe position formula will set probe = 6 which is exactly the 84’s index:
因为84(我们要找的item)大于73(当前的probe位置项),下一步将放弃数组的左边,分配lowEnd= probe+ 1。现在搜索空间只包括84和101。probe位置公式将设置probe= 6,这正好是84的索引。
Since the item we were looking for is found, position 6 will be returned.
由于我们要找的项目已经找到,所以位置6将被返回。
4. Implementation in Java
4.用Java实现
Now that we understood how the algorithm works, let’s implement it in Java.
现在我们了解了该算法的工作原理,让我们用Java来实现它。
First, we initialize lowEnd and highEnd:
首先,我们初始化lowEnd和highEnd。
int highEnd = (data.length - 1);
int lowEnd = 0;Next, we set up a loop and in each iteration, we calculate the new probe based on the aforementioned formula. The loop condition makes sure that we are not out of the search space by comparing item to data[lowEnd] and data[highEnd]:
接下来,我们设置了一个循环,在每次迭代中,我们根据上述公式计算新的probe。循环条件通过将item与data[lowEnd]和data[highEnd]进行比较,确保我们没有离开搜索空间。
while (item >= data[lowEnd] && item <= data[highEnd] && lowEnd <= highEnd) {
int probe
= lowEnd + (highEnd - lowEnd) * (item - data[lowEnd]) / (data[highEnd] - data[lowEnd]);
}We also check if we’ve found the item after every new probe assignment.
我们还在每次新的probe任务后检查是否找到了这个项目。
Finally, we adjust lowEnd or highEnd to decrease the search space on each iteration:
最后,我们调整lowEnd或highEnd以减少每次迭代的搜索空间。
public int interpolationSearch(int[] data, int item) {
int highEnd = (data.length - 1);
int lowEnd = 0;
while (item >= data[lowEnd] && item <= data[highEnd] && lowEnd <= highEnd) {
int probe
= lowEnd + (highEnd - lowEnd) * (item - data[lowEnd]) / (data[highEnd] - data[lowEnd]);
if (highEnd == lowEnd) {
if (data[lowEnd] == item) {
return lowEnd;
} else {
return -1;
}
}
if (data[probe] == item) {
return probe;
}
if (data[probe] < item) {
lowEnd = probe + 1;
} else {
highEnd = probe - 1;
}
}
return -1;
}5. Conclusion
5.结论
In this article, we explored the interpolation search with an example. We implemented it in Java, too.
在这篇文章中,我们用一个例子探讨了插值搜索。我们也用Java实现了它。
The examples shown in this tutorial are available over on Github.
本教程中显示的例子可在Github上找到,。