1. Overview
1.概述
The maximum subarray problem is a task to find the series of contiguous elements with the maximum sum in any given array.
最大子阵列问题是一项任务,即在任何给定的阵列中找到具有最大总和的一系列连续元素。
For instance, in the below array, the highlighted subarray has the maximum sum(6):
例如,在下面的数组中,突出显示的子数组有最大的sum(6):。
In this tutorial, we’ll take a look at two solutions for finding the maximum subarray in an array. One of which we’ll design with O(n) time and space complexity.
在本教程中,我们将看一下寻找数组中最大子阵列的两种解决方案。其中一个我们将以O(n) 时间和空间复杂性来设计。
2. Brute Force Algorithm
2.蛮力算法
Brute force is an iterative approach to solve a problem. In most cases, the solution requires a number of iterations over a data structure. In the next few sections, we’ll apply this approach to solve the maximum subarray problem.
蛮力是解决一个问题的迭代方法。在大多数情况下,解决方案需要在一个数据结构上进行若干次迭代。在接下来的几节中,我们将应用这种方法来解决最大子阵列问题。
2.1. Approach
2.1.方法
Generally speaking, the first solution that comes to mind is to calculate the sum of every possible subarray and return the one with the maximum sum.
一般来说,人们想到的第一个解决方案是计算每个可能的子数组的总和,并返回总和最大的那个。
To begin with, we’ll calculate the sum of every subarray that starts at index 0. And similarly, we’ll find all subarrays starting at every index from 0 to n-1 where n is the length of the array:
首先,我们要计算从索引0开始的每个子数组的总和。同样地,我们将找到从0到n-1每个索引开始的所有子数,其中n是数组的长度。
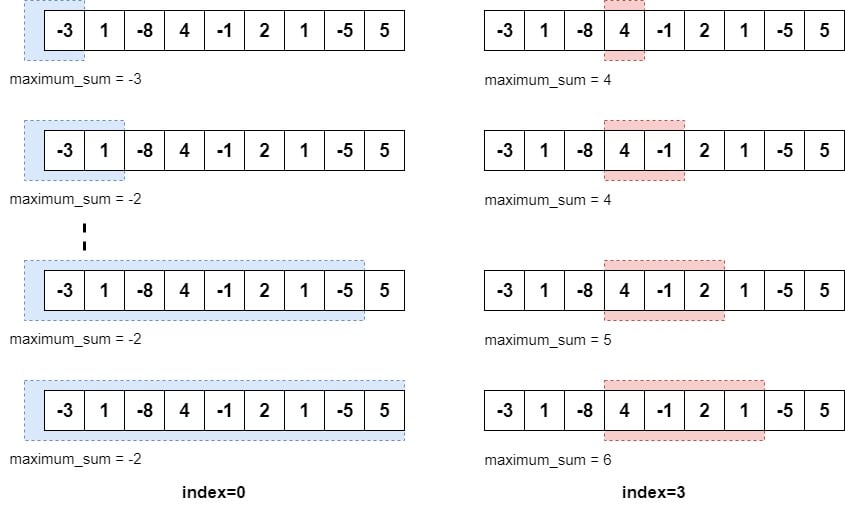
So we’ll start at index 0 and add every element to the running sum in the iteration. We’ll also keep track of the maximum sum seen so far. This iteration is shown on the left side of the image above.
所以我们将从索引0开始,在迭代中把每个元素都加到运行的总和中。我们还将跟踪到目前为止看到的最大和。这个迭代显示在上图的左边。
On the right side of the image, we can see the iteration that starts at index 3. In the last part of this image, we’ve got the subarray with the maximum sum between index 3 and 6.
在图片的右边,我们可以看到从索引3开始的迭代。在这幅图的最后部分,我们已经得到了索引3和6之间具有最大和的子数。
However, our algorithm will continue to find all subarrays starting at indices between 0 and n-1.
然而,我们的算法将继续寻找所有从0和n-1之间索引开始的子数。
2.2. Implementation
2.2.实施
Let’s now see how we can implement this solution in Java:
现在让我们看看如何在Java中实现这个解决方案。
public int maxSubArray(int[] nums) {
int n = nums.length;
int maximumSubArraySum = Integer.MIN_VALUE;
int start = 0;
int end = 0;
for (int left = 0; left < n; left++) {
int runningWindowSum = 0;
for (int right = left; right < n; right++) {
runningWindowSum += nums[right];
if (runningWindowSum > maximumSubArraySum) {
maximumSubArraySum = runningWindowSum;
start = left;
end = right;
}
}
}
logger.info("Found Maximum Subarray between {} and {}", start, end);
return maximumSubArraySum;
}As expected, we update the maximumSubArraySum if the current sum is more than the previous maximum sum. Notably, we then also update the start and end to find out the index locations of this subarray.
正如预期的那样,如果当前的总和超过了之前的最大总和,我们就会更新maximumSubArraySum。值得注意的是,我们随后也会更新start和end来找出这个子数组的索引位置。
2.3. Complexity
2.3.复杂性
Generally speaking the brute force solution iterates over the array many times in order to get every possible solution. This means the time taken by this solution grows quadratically with the number of elements in the array. This may not be a problem for arrays of a small size. But as the size of the array grows, this solution isn’t efficient.
一般来说,暴力解决方法会在数组上迭代多次,以获得所有可能的解决方案。这意味着这个解决方案所花费的时间会随着数组中元素数量的增加而呈二次增长。对于小尺寸的数组来说,这可能不是一个问题。但是随着数组大小的增长,这种解决方案就不那么有效了。
By inspecting the code, we can also see that there are two nested for loops. Therefore, we can conclude that the time complexity of this algorithm is O(n2).
通过检查代码,我们还可以看到,有两个嵌套的for 循环。因此,我们可以得出结论,这个算法的时间复杂度是O(n2)。
In the later sections, we’ll solve this problem in O(n) complexity using dynamic programming.
在后面的章节中,我们将使用动态编程以O(n)的复杂度解决这个问题。
3. Dynamic Programming
3.动态编程
Dynamic programming solves a problem by dividing it into smaller subproblems. This is very similar to the divide-and-conquer algorithm solving technique. The major difference, however, is that dynamic programming solves a subproblem only once.
动态编程通过将一个问题划分为更小的子问题来解决。这与分而治之的算法解决技术非常相似。然而,主要的区别是,动态编程只解决一个子问题一次。
It then stores the result of this subproblem and later reuses this result to solve other related subproblems. This process is known as memoization.
然后,它存储这个子问题的结果,以后再利用这个结果来解决其他相关的子问题。这个过程被称为记忆化。
3.1. Kadane’s Algorithm
3.1.卡丹的算法
Kadane’s algorithm is a popular solution to the maximum subarray problem and this solution is based on dynamic programming.
Kadane算法是最大子阵列问题的一个流行的解决方案,这个解决方案是基于动态编程的。
The most important challenge in solving a dynamic programming problem is to find the optimal subproblems.
解决动态编程问题的最重要挑战是找到最优子问题。
3.2. Approach
3.2.办法
Let’s understand this problem in a different way:
让我们以不同的方式来理解这个问题。
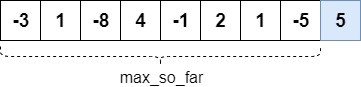
In the image above, we assume that the maximum subarray ends at the last index location. Therefore, the maximum sum of subarray will be:
在上面的图片中,我们假设最大的子阵列在最后一个索引位置结束。因此,子阵列的最大和将是。
maximumSubArraySum = max_so_far + arr[n-1]max_so_far is the maximum sum of a subarray that ends at index n-2. This is also shown in the image above.
max_so_far是指以索引n-2结束的子阵列的最大和。这也显示在上面的图片中。
Now, we can apply this assumption to any index in the array. For example, the maximum subarray sum that ends at n-2 can be calculated as:
现在,我们可以将这个假设应用于数组中的任何索引。例如,结束于n-2的最大子阵列总和可以计算为:。
maximumSubArraySum[n-2] = max_so_far[n-3] + arr[n-2]Therefore, we can conclude that:
因此,我们可以得出结论:。
maximumSubArraySum[i] = maximumSubArraySum[i-1] + arr[i]Now, since every element in the array is a special subarray of size one, we also need to check if an element is greater than the maximum sum itself:
现在,由于数组中的每个元素都是大小为1的特殊子数组,我们还需要检查一个元素是否大于最大和本身。
maximumSubArraySum[i] = Max(arr[i], maximumSubArraySum[i-1] + arr[i])By looking at these equations, we can see that we need to find the maximum subarray sum at every index of the array. Thus, we divided our problem into n subproblems. We can find the maximum sum at every index by iterating the array only once:
通过观察这些方程,我们可以看到,我们需要找到数组中每个索引的最大子数组之和。因此,我们把问题分为n个子问题。我们可以通过只迭代一次数组来找到每个索引的最大和。
The highlighted element shows the current element in the iteration. At every index, we’ll apply the equation derived earlier to calculate a value for max_ending_here. This helps us in identifying whether we should include the current element in the subarray or start a new subarray starting at this index.
突出显示的元素是迭代中的当前元素。在每个索引,我们将应用前面得出的方程式来计算max_ending_here的值。这有助于我们确定我们是否应该将当前元素包含在子阵列中,或者从这个索引开始启动一个新的子阵列。
Another variable, max_so_far is used to store the maximum subarray sum found during the iteration. Once we iterate over the last index, max_so_far will store the sum of the maximum subarray.
另一个变量,max_so_far是用来存储迭代过程中发现的最大子阵列之和。一旦我们迭代到最后一个索引,max_so_far将存储最大子阵列的和。
3.3. Implementation
3.3.实施
Again, let’s see how we can now implement the Kadane algorithm in Java, following the above approach:
同样,让我们看看现在我们如何按照上述方法在Java中实现Kadane算法。
public int maxSubArraySum(int[] arr) {
int size = arr.length;
int start = 0;
int end = 0;
int maxSoFar = arr[0], maxEndingHere = arr[0];
for (int i = 1; i < size; i++) {
if (arr[i] > maxEndingHere + arr[i]) {
start = i;
maxEndingHere = arr[i];
} else
maxEndingHere = maxEndingHere + arr[i];
if (maxSoFar < maxEndingHere) {
maxSoFar = maxEndingHere;
end = i;
}
}
logger.info("Found Maximum Subarray between {} and {}", Math.min(start, end), end);
return maxSoFar;
}Here, we updated the start and end to find the maximum subarray indices.
在这里,我们更新了开始和结束,以找到最大的子阵列索引。
Note that we take Math.min(start, end) instead of start as the start index of the maximum subarray. This is because, if the array contains only negative numbers, the maximum subarray would be the largest element itself. In this case, if (arr[i] > maxEndingHere + arr[i]) will always be true. That is, the value of start is greater than the value of end.
注意,我们取Math.min(start, end)而不是start作为最大子阵列的起始索引。这是因为,如果数组只包含负数,最大子数组将是最大元素本身。在这种情况下,if (arr[i] > maxEndingHere + arr[i])将始终是true。也就是说,start的值大于end的值。
3.4. Complexity
3.4.复杂性
Since we only need to iterate the array once, the time complexity of this algorithm is O(n).
由于我们只需要对数组进行一次迭代,这个算法的时间复杂度为O(n)。
So as we can see, the time taken by this solution grows linearly with the number of elements in the array. Consequently, it is more efficient than the brute force approach we discussed in the last section.
所以我们可以看到,这个解决方案所花费的时间与数组中的元素数量呈线性增长。因此,它比我们在上一节讨论的蛮力方法更有效率。
4. Conclusion
4.总结
In this quick tutorial, we’ve described two ways to solve the maximum subarray problem.
在这个快速教程中,我们介绍了解决最大子阵列问题的两种方法。
First, we explored a brute force approach and saw that this iterative solution resulted in quadratic time. Later, we then discussed the Kadane algorithm and used dynamic programming to solve the problem in linear time.
首先,我们探索了一种蛮力方法,并看到这种迭代式的解决方案导致了四次方的时间。后来,我们又讨论了Kadane算法,并使用动态编程在线性时间内解决这个问题。
As always, the full source code of the article is available over on GitHub.
一如既往,文章的完整源代码可在GitHub上获得。