1. Introduction
1.绪论
In this tutorial, we’re going to learn how to merge two sorted arrays into a single sorted array.
在本教程中,我们将学习如何将两个排序的数组合并成一个排序的数组。
2. Problem
2 问题
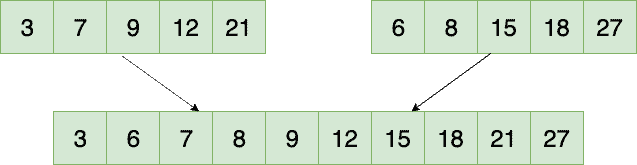
Let’s understand the problem. We have two sorted arrays and we would like to merge them into one.
让我们了解一下这个问题。我们有两个排序的数组,我们想把它们合并成一个。
3. Algorithm
3.算法
When we analyze the problem, it’s quite easy to observe that we can solve this problem by using the merge operation of Merge Sort.
当我们分析这个问题时,很容易观察到,我们可以通过使用合并排序的合并操作来解决这个问题。。
Let’s say we have two sorted arrays foo and bar of length fooLength and barLength, respectively. Next, we can declare another array merged of size fooLength + barLength.
假设我们有两个排序的数组foo和bar,长度分别为fooLength和barLength。接下来,我们可以声明另一个数组merged,其大小为fooLength + barLength。
We should then traverse both of the arrays in the same loop. We’ll maintain a current index value for each, fooPosition and barPosition. On a given iteration of our loop, we take whichever array has the smaller-valued element at their index and advance that index. This element will occupy the next position in the merged array.
然后我们应该在同一个循环中遍历这两个数组。我们将为每个数组保持一个当前的索引值,fooPosition和barPosition。在我们的循环的一个给定的迭代中,我们从数组的索引中选取数值较小的元素,并推进该索引。
Finally, once we’ve transferred all elements from one array, we’ll copy the remaining from the other into the merged array.
最后,一旦我们从一个数组中转移了所有的元素,我们将从另一个数组中复制剩余的元素到合并的数组。
Now let’s see the process in pictures to better understand the algorithm.
现在让我们用图片来看看这个过程,以便更好地理解这个算法。
Step 1:
第1步:
We start by comparing the elements in both the arrays, and we pick the smaller one.
我们首先比较两个数组中的元素,然后挑选较小的那个。
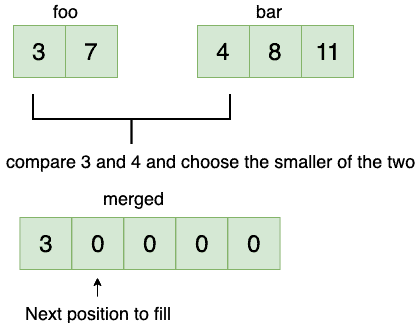
Then we increment the position in the first array.
然后我们增加first数组中的位置。
Step 2:
第2步:。
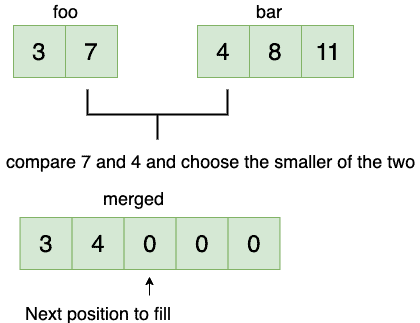
Here we increment the position in the second array and move on to the next element which is 8.
在这里,我们增加第二个数组中的位置,然后转到下一个元素,也就是8。
Step 3:
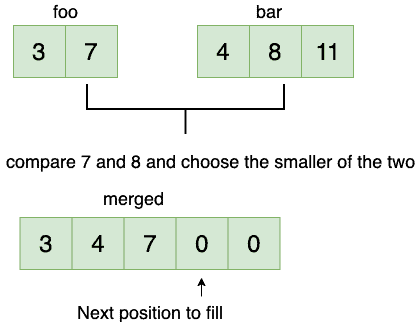
第三步:

At the end of this iteration, we’ve traversed all the elements of the first array.
在这个迭代的最后,我们已经遍历了first数组的所有元素。
Step 4:
第4步:
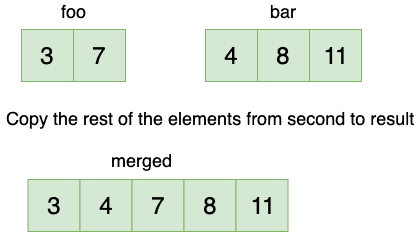
In this step, we just copy all the remaining elements from the second array to result.
在这一步,我们只是将第二个数组中的所有剩余元素复制到result。
4. Implementation
4.实施
Now let’s see how to implement it:
现在让我们来看看如何实现它。
public static int[] merge(int[] foo, int[] bar) {
int fooLength = foo.length;
int barLength = bar.length;
int[] merged = new int[fooLength + barLength];
int fooPosition, barPosition, mergedPosition;
fooPosition = barPosition = mergedPosition = 0;
while(fooPosition < fooLength && barPosition < barLength) {
if (foo[fooPosition] < bar[barPosition]) {
merged[mergedPosition++] = foo[fooPosition++];
} else {
merged[mergedPosition++] = bar[barPosition++];
}
}
while (fooPosition < fooLength) {
merged[mergedPosition++] = foo[fooPosition++];
}
while (barPosition < barLength) {
merged[mergedPosition++] = bar[barPosition++];
}
return merged;
}And let’s proceed with a brief test:
而让我们继续进行一个简短的测试。
@Test
public void givenTwoSortedArrays_whenMerged_thenReturnMergedSortedArray() {
int[] foo = { 3, 7 };
int[] bar = { 4, 8, 11 };
int[] merged = { 3, 4, 7, 8, 11 };
assertArrayEquals(merged, SortedArrays.merge(foo, bar));
}5. Complexity
5.复杂性
We traverse both the arrays and choose the smaller element. In the end, we copy the rest of the elements from the foo or the bar array. So the time complexity becomes O(fooLength + barLength). We’ve used an auxiliary array to obtain the result. So the space complexity is also O(fooLength + barLength).
我们遍历两个数组并选择较小的元素。最后,我们从foo或bar数组中复制其余元素。所以时间复杂度变成了O(fooLength + barLength)。我们使用了一个辅助数组来获得结果。所以空间复杂度也是O(fooLength + barLength)。
6. Conclusion
6.结语
In this tutorial, we learned how to merge two sorted arrays into one.
在本教程中,我们学习了如何将两个排序的数组合并成一个。
As usual, the source code for this tutorial can be found over on GitHub.
像往常一样,本教程的源代码可以在GitHub上找到。