1. Overview
1.概述
In this short tutorial, we’ll see how we can efficiently merge sorted arrays using a heap.
在这个简短的教程中,我们将看到我们如何使用堆来有效地合并排序的数组。
2. The Algorithm
2.算法
Since our problem statement is to use a heap to merge the arrays, we’ll use a min-heap to solve our problem. A min-heap is nothing but a binary tree in which the value of each node is smaller than the values of its child nodes.
由于我们的问题陈述是使用堆来合并数组,我们将使用最小堆来解决问题。最小堆只不过是一个二进制树,其中每个节点的值都小于其子节点的值。
Usually, the min-heap is implemented using an array in which the array satisfies specific rules when it comes to finding the parent and children of a node.
通常,迷你堆是用一个数组来实现的,在寻找节点的父和子时,数组要满足特定的规则。
For an array A[] and an element at index i:
对于一个数组A[]和一个位于索引i的元素。
- A[(i-1)/2] will return its parent
- A[(2*i)+1] will return the left child
- A[(2*i)+2] will return the right child
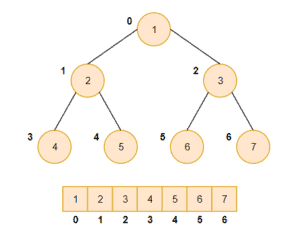
Here’s a picture of min-heap and its array representation:
这里有一张min-heap的图片和它的数组表示。
Let’s now create our algorithm that merges a set of sorted arrays:
现在让我们创建我们的算法,将一组排序的数组合并。
- Create an array to store the results, with the size determined by adding the length of all the input arrays.
- Create a second array of size equal to the number of input arrays, and populate it with the first elements of all the input arrays.
- Transform the previously created array into a min-heap by applying the min-heap rules on all nodes and their children.
- Repeat the next steps until the result array is fully populated.
- Get the root element from the min-heap and store it in the result array.
- Replace the root element with the next element from the array in which the current root is populated.
- Apply min-heap rule again on our min-heap array.
Our algorithm has a recursive flow to create the min-heap, and we have to visit all the elements of the input arrays.
我们的算法有一个递归流程来创建最小堆,而且我们必须访问输入数组的所有元素。
The time complexity of this algorithm is O(k log n), where k is the total number of elements in all the input arrays, and n is the total number of sorted arrays.
这个算法的时间complexity是O(k log n),其中k是所有输入数组中元素的总数,和n是排序数组的总数。
Let’s now see a sample input and the expected result after running the algorithm so that we can gain a better understanding of the problem. So for these arrays:
现在让我们看看输入样本和运行算法后的预期结果,这样我们就能对问题有更好的理解。那么对于这些数组
{ { 0, 6 }, { 1, 5, 10, 100 }, { 2, 4, 200, 650 } }The algorithm should return a result array:
该算法应该返回一个结果数组。
{ 0, 1, 2, 4, 5, 6, 10, 100, 200, 650 }3. Java Implementation
3.Java实现
Now that we have a basic understanding of what a min-heap is and how the merge algorithm works, let’s look at the Java implementation. We’ll use two classes — one to represent the heap nodes and the other to implement the merge algorithm.
现在我们对什么是迷你堆以及合并算法如何工作有了基本的了解,让我们看看Java的实现。我们将使用两个类–一个用来表示堆节点,另一个用来实现合并算法。
3.1. Heap Node Representation
3.1.堆节点表示法
Before implementing the algorithm itself, let’s create a class that represents a heap node. This will store the node value and two supporting fields:
在实现算法本身之前,让我们创建一个代表堆节点的类。这将存储节点的值和两个支持字段。
public class HeapNode {
int element;
int arrayIndex;
int nextElementIndex = 1;
public HeapNode(int element, int arrayIndex) {
this.element = element;
this.arrayIndex = arrayIndex;
}
}Note that we’ve purposefully omitted the getters and setters here to keep things simple. We’ll use the arrayIndex property to store the index of the array in which the current heap node element is taken. And we’ll use the nextElementIndex property to store the index of the element that we’ll be taking after moving the root node to the result array.
注意,我们特意在这里省略了getters和setters,以保持简单。我们将使用arrayIndex属性来存储当前堆节点元素所处的数组的索引。我们将使用nextElementIndex属性来存储我们在将根节点移到结果数组中后要取的元素的索引。
Initially, the value of nextElementIndex will be 1. We’ll be incrementing its value after replacing the root node of the min-heap.
最初,nextElementIndex的值将是1。我们将在替换了min-heap的根节点后增加它的值。
3.2. Min-Heap Merge Algorithm
3.2.最小海普合并算法
Our next class is to represent the min-heap itself and to implement the merge algorithm:
我们的下一个类别是表示迷你堆本身,并实现合并算法。
public class MinHeap {
HeapNode[] heapNodes;
public MinHeap(HeapNode heapNodes[]) {
this.heapNodes = heapNodes;
heapifyFromLastLeafsParent();
}
int getParentNodeIndex(int index) {
return (index - 1) / 2;
}
int getLeftNodeIndex(int index) {
return (2 * index + 1);
}
int getRightNodeIndex(int index) {
return (2 * index + 2);
}
HeapNode getRootNode() {
return heapNodes[0];
}
// additional implementation methods
}Now that we’ve created our min-heap class, let’s add a method that will heapify a subtree where the root node of the subtree is at the given index of the array:
现在我们已经创建了min-heap类,让我们添加一个方法来堆积一个子树,其中子树的根节点位于数组的给定索引处。
void heapify(int index) {
int leftNodeIndex = getLeftNodeIndex(index);
int rightNodeIndex = getRightNodeIndex(index);
int smallestElementIndex = index;
if (leftNodeIndex < heapNodes.length
&& heapNodes[leftNodeIndex].element < heapNodes[index].element) {
smallestElementIndex = leftNodeIndex;
}
if (rightNodeIndex < heapNodes.length
&& heapNodes[rightNodeIndex].element < heapNodes[smallestElementIndex].element) {
smallestElementIndex = rightNodeIndex;
}
if (smallestElementIndex != index) {
swap(index, smallestElementIndex);
heapify(smallestElementIndex);
}
}When we use an array to represent a min-heap, the last leaf node will always be at the end of the array. So when transforming an array into a min-heap by calling the heapify() method iteratively, we only need to start the iteration from the last leaf’s parent node:
当我们用一个数组来表示一个最小堆时,最后一个叶子节点将总是在数组的末端。因此,当通过反复调用heapify()方法将数组转换为最小堆时,我们只需要从最后一个叶子的父节点开始迭代。
void heapifyFromLastLeafsParent() {
int lastLeafsParentIndex = getParentNodeIndex(heapNodes.length);
while (lastLeafsParentIndex >= 0) {
heapify(lastLeafsParentIndex);
lastLeafsParentIndex--;
}
}Our next method will do the actual implementation of our algorithm. For our better understanding, let’s split the method into two parts and see how it works:
我们的下一个方法将对我们的算法进行实际实现。为了让我们更好地理解,让我们把这个方法分成两部分,看看它是如何工作的。
int[] merge(int[][] array) {
// transform input arrays
// run the minheap algorithm
// return the resulting array
}The first part transforms the input arrays into a heap node array that contains all the first array’s elements and finds the resulting array’s size:
第一部分将输入的数组转化为包含第一个数组所有元素的堆节点数组,并找出所产生的数组的大小。
HeapNode[] heapNodes = new HeapNode[array.length];
int resultingArraySize = 0;
for (int i = 0; i < array.length; i++) {
HeapNode node = new HeapNode(array[i][0], i);
heapNodes[i] = node;
resultingArraySize += array[i].length;
}And the next part populates the result array by implementing the steps 4, 5, 6, and 7 of our algorithm:
而下一部分通过实现我们算法的第4、5、6和7步来填充结果数组。
MinHeap minHeap = new MinHeap(heapNodes);
int[] resultingArray = new int[resultingArraySize];
for (int i = 0; i < resultingArraySize; i++) {
HeapNode root = minHeap.getRootNode();
resultingArray[i] = root.element;
if (root.nextElementIndex < array[root.arrayIndex].length) {
root.element = array[root.arrayIndex][root.nextElementIndex++];
} else {
root.element = Integer.MAX_VALUE;
}
minHeap.heapify(0);
}4. Testing the Algorithm
4.测试算法
Let’s now test our algorithm with the same input we mentioned previously:
现在让我们用之前提到的相同输入来测试我们的算法。
int[][] inputArray = { { 0, 6 }, { 1, 5, 10, 100 }, { 2, 4, 200, 650 } };
int[] expectedArray = { 0, 1, 2, 4, 5, 6, 10, 100, 200, 650 };
int[] resultArray = MinHeap.merge(inputArray);
assertThat(resultArray.length, is(equalTo(10)));
assertThat(resultArray, is(equalTo(expectedArray)));5. Conclusion
5.结论
In this tutorial, we learned how we can efficiently merge sorted arrays using min-heap.
在本教程中,我们学习了如何使用min-heap高效合并排序数组。
The example we’ve demonstrated here can be found over on GitHub.
我们在这里演示的例子可以在GitHub上找到over。