1. Overview
1.概述
In this tutorial, we’ll explore the concept of pattern matching of strings and how we can make it faster. Then, we’ll walk through its implementation in Java.
在本教程中,我们将探讨字符串模式匹配的概念以及如何使其更快。然后,我们将介绍其在Java中的实现。
2. Pattern Matching of Strings
2.字符串的模式匹配
2.1. Definition
2.1 定义
In strings, pattern matching is the process of checking for a given sequence of characters called a pattern in a sequence of characters called a text.
在字符串中,模式匹配是在称为文本的字符序列中检查给定的字符序列的过程,称为模式。
The basic expectations of pattern matching when the pattern is not a regular expression are:
当模式不是正则表达式时,模式匹配的基本期望是。
- the match should be exact – not partial
- the result should contain all matches – not just the first match
- the result should contain the position of each match within the text
2.2. Searching for a Pattern
2.2.搜索一个模式
Let’s use an example to understand a simple pattern matching problem:
让我们用一个例子来理解一个简单的模式匹配问题。
Pattern: NA
Text: HAVANABANANA
Match1: ----NA------
Match2: --------NA--
Match3: ----------NAWe can see that the pattern NA occurs three times in the text. To get this result, we can think of sliding the pattern down the text one character at a time and checking for a match.
我们可以看到,模式NA在文本中出现了三次。为了得到这个结果,我们可以考虑将该模式在文本中一次一次地滑动,并检查是否匹配。
However, this is a brute-force approach with time complexity O(p*t) where p is the length of the pattern, and t is the length of text.
然而,这是一种粗暴的方法,时间复杂度O(p*t),其中p是模式的长度,t是文本的长度。
Suppose we have more than one pattern to search for. Then, the time complexity also increases linearly as each pattern will need a separate iteration.
假设我们有一个以上的模式需要搜索。那么,时间复杂性也会线性增加,因为每个模式都需要单独的迭代。
2.3. Trie Data Structure to Store Patterns
2.3.用于存储模式的Trie数据结构
We can improve the search time by storing the patterns in a trie data structure, which is known for its fast retrieval of items.
我们可以通过将模式存储在trie数据结构中来改善搜索时间,该结构以快速重新trie评估项目而闻名。
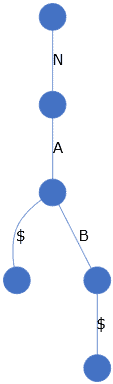
We know that a trie data structure stores the characters of a string in a tree-like structure. So, for two strings {NA, NAB}, we will get a tree with two paths:
我们知道,Trie数据结构以树状结构存储字符串的字符。因此,对于两个字符串{NA, NAB},我们将得到一个有两条路径的树。
Having a trie created makes it possible to slide a group of patterns down the text and check for matches in just one iteration.
有了创建的Trie,就有可能在文本中滑动一组模式,并在一次迭代中检查是否匹配。
Notice that we use the $ character to indicate the end of the string.
注意,我们使用$字符来表示字符串的结束。
2.4. Suffix Trie Data Structure to Store Text
2.4.储存文本的后缀Trie数据结构
A suffix trie, on the other hand, is a trie data structure constructed using all possible suffixes of a single string.
另一方面,后缀 trie是一个 trie 数据结构,使用单个字符串的所有可能的后缀来构建。
For the previous example HAVANABANANA, we can construct a suffix trie:
对于前面的例子HAVANABANANA,我们可以构建一个后缀trie。
Suffix tries are created for the text and are usually done as part of a pre-processing step. After that, searching for patterns can be done quickly by finding a path matching the pattern sequence.
后缀尝试是为文本创建的,通常作为预处理步骤的一部分进行。之后,搜索模式可以通过寻找与模式序列相匹配的路径快速完成。
However, a suffix trie is known to consume a lot of space as each character of the string is stored in an edge.
然而,众所周知,后缀三元组会消耗大量的空间,因为字符串的每个字符都被存储在一个边上。
We’ll look at an improved version of the suffix trie in the next section.
我们将在下一节看一下后缀TREE的改进版本。
3. Suffix Tree
3.词缀树
A suffix tree is simply a compressed suffix trie. What this means is that, by joining the edges, we can store a group of characters and thereby reduce the storage space significantly.
后缀tree只是一个压缩的后缀trie。这意味着,通过连接边缘,我们可以存储一组字符,从而大大减少存储空间。
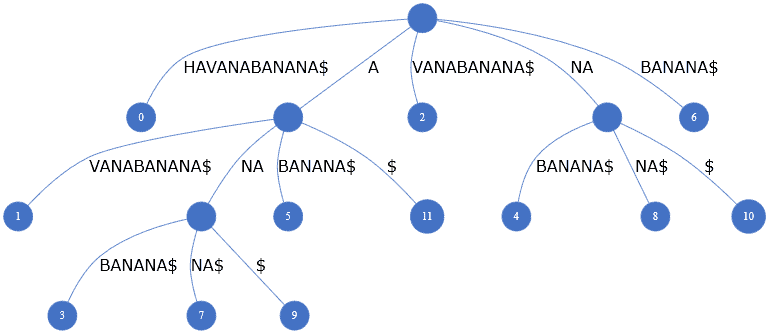
So, we can create a suffix tree for the same text HAVANABANANA:
因此,我们可以为同一个文本HAVANABANANA创建一个后缀树。
Every path starting from the root to the leaf represents a suffix of the string HAVANABANANA.
从根开始到叶的每条路径都代表了字符串HAVANABANANA的后缀。
A suffix tree also stores the position of the suffix in the leaf node. For example, BANANA$ is a suffix starting from the seventh position. Hence, its value will be six using zero-based numbering. Likewise, A->BANANA$ is another suffix starting at position five, as we see in the above picture.
后缀树还存储了叶子节点中后缀的位置。例如,BANANA$是一个从第七个位置开始的后缀。因此,它的值将是使用基于零的编号的六。同样,A->BANANA$是另一个从第五位开始的后缀,正如我们在上图中看到的。
So, putting things into perspective, we can see that a pattern match occurs when we’re able to get a path starting from the root node with edges fully matching the given pattern positionally.
因此,把事情看清楚,我们可以看到,当我们能够得到一条从根节点开始的路径,其边缘在位置上完全匹配给定的模式时,就会发生模式匹配。
If the path ends at a leaf node, we get a suffix match. Otherwise, we get just a substring match. For example, the pattern NA is a suffix of HAVANABANA[NA] and a substring of HAVA[NA]BANANA.
如果路径在一个叶子节点结束,我们得到一个后缀匹配。否则,我们只得到一个子串匹配。例如,模式NA是HAVANABANA[NA]的后缀和HAVA[NA]BANANA的子串。
In the next section, we’ll see how to implement this data structure in Java.
在下一节,我们将看到如何在Java中实现这种数据结构。
4. Data Structure
4.数据结构
Let’s create a suffix tree data structure. We’ll need two domain classes.
让我们来创建一个后缀树数据结构。我们将需要两个域类。
Firstly, we need a class to represent the tree node. It needs to store the tree’s edges and its child nodes. Additionally, when it’s a leaf node, it needs to store the positional value of the suffix.
首先,我们需要一个类来表示树节点。它需要存储树的边和它的子节点。此外,当它是一个叶子节点时,它需要存储后缀的位置值。
So, let’s create our Node class:
所以,让我们来创建我们的Node类。
public class Node {
private String text;
private List<Node> children;
private int position;
public Node(String word, int position) {
this.text = word;
this.position = position;
this.children = new ArrayList<>();
}
// getters, setters, toString()
}Secondly, we need a class to represent the tree and store the root node. It also needs to store the full text from which the suffixes are generated.
其次,我们需要一个类来表示树并存储根节点。它还需要存储生成后缀的全文。
Consequently, we have a SuffixTree class:
因此,我们有一个SuffixTree类。
public class SuffixTree {
private static final String WORD_TERMINATION = "$";
private static final int POSITION_UNDEFINED = -1;
private Node root;
private String fullText;
public SuffixTree(String text) {
root = new Node("", POSITION_UNDEFINED);
fullText = text;
}
}5. Helper Methods for Adding Data
5.添加数据的帮助方法
Before we write our core logic to store data, let’s add a few helper methods. These will prove useful later.
在我们编写存储数据的核心逻辑之前,让我们添加一些辅助方法。这些将在以后被证明是有用的。
Let’s modify our SuffixTree class to add some methods needed for constructing the tree.
让我们修改我们的SuffixTree类,添加一些构建树所需的方法。
5.1. Adding a Child Node
5.1.添加一个子节点
Firstly, let’s have a method addChildNode to add a new child node to any given parent node:
首先,让我们有一个方法addChildNode来向任何给定的父节点添加一个新的子节点。
private void addChildNode(Node parentNode, String text, int index) {
parentNode.getChildren().add(new Node(text, index));
}5.2. Finding Longest Common Prefix of Two Strings
5.2.寻找两个字符串的最长共同前缀
Secondly, we’ll write a simple utility method getLongestCommonPrefix to find the longest common prefix of two strings:
其次,我们将编写一个简单的实用方法getLongestCommonPrefix来寻找两个字符串的最长共同前缀。
private String getLongestCommonPrefix(String str1, String str2) {
int compareLength = Math.min(str1.length(), str2.length());
for (int i = 0; i < compareLength; i++) {
if (str1.charAt(i) != str2.charAt(i)) {
return str1.substring(0, i);
}
}
return str1.substring(0, compareLength);
}5.3. Splitting a Node
5.3.分割一个节点
Thirdly, let’s have a method to carve out a child node from a given parent. In this process, the parent node’s text value will get truncated, and the right-truncated string becomes the text value of the child node. Additionally, the children of the parent will get transferred to the child node.
第三,让我们有一个方法来从一个给定的父节点中挖出一个子节点。在这个过程中,父节点的text值将被截断,被截断的字符串成为子节点的text值。此外,父节点的子节点将被转移到子节点上。
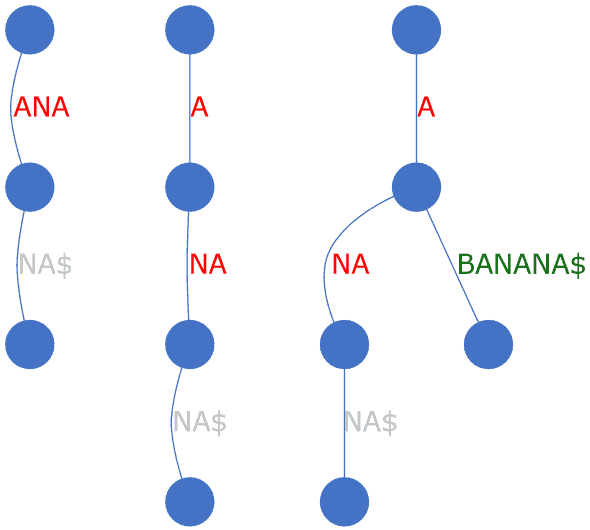
We can see from the picture below that ANA gets split to A->NA. Afterward, the new suffix ABANANA$ can be added as A->BANANA$:
我们可以从下图中看到,ANA被分割成A->NA.之后,新的后缀ABANANA$可以被添加为A->BANANA$。
In short, this is a convenience method that will come in handy when inserting a new node:
简而言之,这是一个方便的方法,在插入一个新的节点时将会很方便。
private void splitNodeToParentAndChild(Node parentNode, String parentNewText, String childNewText) {
Node childNode = new Node(childNewText, parentNode.getPosition());
if (parentNode.getChildren().size() > 0) {
while (parentNode.getChildren().size() > 0) {
childNode.getChildren()
.add(parentNode.getChildren().remove(0));
}
}
parentNode.getChildren().add(childNode);
parentNode.setText(parentNewText);
parentNode.setPosition(POSITION_UNDEFINED);
}6. Helper Method for Traversal
6.遍历的帮助方法
Let’s now create the logic to traverse the tree. We’ll use this method for both constructing the tree and searching for patterns.
现在让我们创建一个逻辑来遍历这棵树。我们将使用这个方法来构建树和搜索模式。
6.1. Partial Match vs. Full Match
6.1 部分匹配与完全匹配
First, let’s understand the concept of a partial match and a full match by considering a tree populated with a few suffixes:
首先,让我们通过考虑一棵由几个后缀填充的树来理解部分匹配和完全匹配的概念。
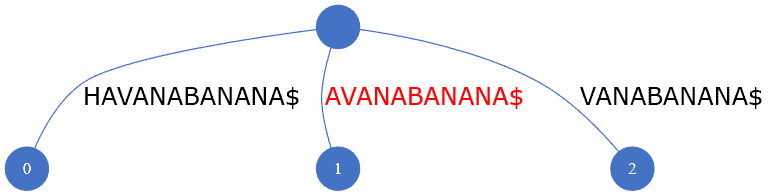
To add a new suffix ANABANANA$, we check if any node exists that can be modified or extended to accommodate the new value. For this, we compare the new text with all the nodes and find that the existing node [A]VANABANANA$ matches at first character. So, this is the node we need to modify, and this match can be called a partial match.
为了增加一个新的后缀ANABANANA$,我们检查是否有任何节点存在可以被修改或扩展以适应新的值。为此,我们将新文本与所有节点进行比较,发现现有节点[A]VANABANANA$在第一个字符处是匹配的。所以,这就是我们需要修改的节点,这种匹配可以称为部分匹配。
On the other hand, let’s consider that we’re searching for the pattern VANE on the same tree. We know that it partially matches with [VAN]ABANANA$ on the first three characters. If all the four characters had matched, we could call it a full match. For pattern search, a complete match is necessary.
另一方面,让我们考虑一下,我们正在同一棵树上搜索模式VANE。我们知道,它与[VAN]ABANANA$的前三个字符部分匹配。如果所有四个字符都匹配,我们可以称其为完全匹配。对于模式搜索,完全匹配是必要的。
So to summarize, we’ll use a partial match when constructing the tree and a full match when searching for patterns. We’ll use a flag isAllowPartialMatch to indicate the kind of match we need in each case.
所以总结一下,我们在构建树的时候会使用部分匹配,在搜索模式的时候会使用完全匹配。我们将使用一个标志isAllowPartialMatch来指示我们在每种情况下需要的匹配类型。
6.2. Traversing the Tree
6.2.遍历树
Now, let’s write our logic to traverse the tree as long as we’re able to match a given pattern positionally:
现在,让我们写下我们的逻辑,只要我们能够在位置上匹配一个给定的模式,就可以遍历这棵树。
List<Node> getAllNodesInTraversePath(String pattern, Node startNode, boolean isAllowPartialMatch) {
// ...
}We’ll call this recursively and return a list of all the nodes we find in our path.
我们将递归地调用这个,并返回一个我们在路径中找到的所有节点的列表。
We start by comparing the first character of the pattern text with the node text:
我们首先将模式文本的第一个字符与节点文本进行比较。
if (pattern.charAt(0) == nodeText.charAt(0)) {
// logic to handle remaining characters
}
For a partial match, if the pattern is shorter or equal in length to the node text, we add the current node to our nodes list and stop here:
对于部分匹配,如果模式短于或等于节点文本的长度,我们将当前节点添加到我们的nodes列表中并在此停止。
if (isAllowPartialMatch && pattern.length() <= nodeText.length()) {
nodes.add(currentNode);
return nodes;
}
Then we compare the remaining characters of this node text with that of the pattern. If the pattern has a positional mismatch with the node text, we stop here. The current node is included in nodes list only for a partial match:
然后,我们将该节点文本的剩余字符与该模式的剩余字符进行比较。如果模式与节点文本有位置上的不匹配,我们就在此停止。只有在部分匹配的情况下,当前节点才会被包含在nodes列表中。
int compareLength = Math.min(nodeText.length(), pattern.length());
for (int j = 1; j < compareLength; j++) {
if (pattern.charAt(j) != nodeText.charAt(j)) {
if (isAllowPartialMatch) {
nodes.add(currentNode);
}
return nodes;
}
}
If the pattern matched the node text, we add the current node to our nodes list:
如果模式与节点文本相匹配,我们就将当前节点添加到我们的nodes列表中。
nodes.add(currentNode);But if the pattern has more characters than the node text, we need to check the child nodes. For this, we make a recursive call passing the currentNode as the starting node and remaining portion of the pattern as the new pattern. The list of nodes returned from this call is appended to our nodes list if it’s not empty. In case it’s empty for a full match scenario, it means there was a mismatch, so to indicate this, we add a null item. And we return the nodes:
但是,如果模式的字符比节点文本多,我们需要检查子节点。为此,我们进行一个递归调用,将currentNode作为起始节点,将pattern的剩余部分作为新模式。如果我们的nodes列表不是空的,这个调用返回的节点列表将被追加到我们的nodes列表。如果它在完全匹配的情况下是空的,这意味着有一个不匹配,所以为了表明这一点,我们添加一个null项。然后我们返回nodes。
if (pattern.length() > compareLength) {
List nodes2 = getAllNodesInTraversePath(pattern.substring(compareLength), currentNode,
isAllowPartialMatch);
if (nodes2.size() > 0) {
nodes.addAll(nodes2);
} else if (!isAllowPartialMatch) {
nodes.add(null);
}
}
return nodes;Putting all this together, let’s create getAllNodesInTraversePath:
把所有这些放在一起,让我们创建getAllNodesInTraversePath。
private List<Node> getAllNodesInTraversePath(String pattern, Node startNode, boolean isAllowPartialMatch) {
List<Node> nodes = new ArrayList<>();
for (int i = 0; i < startNode.getChildren().size(); i++) {
Node currentNode = startNode.getChildren().get(i);
String nodeText = currentNode.getText();
if (pattern.charAt(0) == nodeText.charAt(0)) {
if (isAllowPartialMatch && pattern.length() <= nodeText.length()) {
nodes.add(currentNode);
return nodes;
}
int compareLength = Math.min(nodeText.length(), pattern.length());
for (int j = 1; j < compareLength; j++) {
if (pattern.charAt(j) != nodeText.charAt(j)) {
if (isAllowPartialMatch) {
nodes.add(currentNode);
}
return nodes;
}
}
nodes.add(currentNode);
if (pattern.length() > compareLength) {
List<Node> nodes2 = getAllNodesInTraversePath(pattern.substring(compareLength),
currentNode, isAllowPartialMatch);
if (nodes2.size() > 0) {
nodes.addAll(nodes2);
} else if (!isAllowPartialMatch) {
nodes.add(null);
}
}
return nodes;
}
}
return nodes;
}7. Algorithm
7.算法
7.1. Storing Data
7.1.储存数据
We can now write our logic to store data. Let’s start by defining a new method addSuffix on the SuffixTree class:
我们现在可以编写我们的逻辑来存储数据。让我们先在SuffixTree类上定义一个新方法addSuffix。
private void addSuffix(String suffix, int position) {
// ...
}The caller will provide the position of the suffix.
调用者将提供后缀的位置。
Next, let’s write the logic to handle the suffix. First, we need to check if a path exists matching the suffix partially at least by calling our helper method getAllNodesInTraversePath with isAllowPartialMatch set as true. If no path exists, we can add our suffix as a child to the root:
接下来,让我们编写处理后缀的逻辑。首先,我们需要至少通过调用我们的辅助方法getAllNodesInTraversePath并将isAllowPartialMatch设置为true,来检查是否存在与后缀部分匹配的路径。如果没有路径存在,我们可以把我们的后缀作为根的一个子节点加入。
List<Node> nodes = getAllNodesInTraversePath(pattern, root, true);
if (nodes.size() == 0) {
addChildNode(root, suffix, position);
}However, if a path exists, it means we need to modify an existing node. This node will be the last one in the nodes list. We also need to figure out what should be the new text for this existing node. If the nodes list has only one item, then we use the suffix. Otherwise, we exclude the common prefix up to the last node from the suffix to get the newText:
然而,如果存在一个路径,这意味着我们需要修改一个现有的节点。这个节点将是nodes 列表中的最后一个节点。我们还需要弄清楚这个现有节点的新文本应该是什么。如果nodes列表中只有一个项目,那么我们就使用suffix。否则,我们从suffix中排除到最后一个节点的普通前缀,得到newText。
Node lastNode = nodes.remove(nodes.size() - 1);
String newText = suffix;
if (nodes.size() > 0) {
String existingSuffixUptoLastNode = nodes.stream()
.map(a -> a.getText())
.reduce("", String::concat);
newText = newText.substring(existingSuffixUptoLastNode.length());
}For modifying the existing node, let’s create a new method extendNode, which we’ll call from where we left off in addSuffix method. This method has two key responsibilities. One is to break up an existing node to parent and child, and the other is to add a child to the newly created parent node. We break up the parent node only to make it a common node for all its child nodes. So, our new method is ready:
为了修改现有的节点,让我们创建一个新的方法extendNode,,我们将从addSuffix方法的地方调用它。这个方法有两个关键职责。一个是将现有的节点分解为父节点和子节点,另一个是向新创建的父节点添加一个子节点。我们拆分父节点只是为了让它成为所有子节点的共同节点。所以,我们的新方法已经准备好了。
private void extendNode(Node node, String newText, int position) {
String currentText = node.getText();
String commonPrefix = getLongestCommonPrefix(currentText, newText);
if (commonPrefix != currentText) {
String parentText = currentText.substring(0, commonPrefix.length());
String childText = currentText.substring(commonPrefix.length());
splitNodeToParentAndChild(node, parentText, childText);
}
String remainingText = newText.substring(commonPrefix.length());
addChildNode(node, remainingText, position);
}We can now come back to our method for adding a suffix, which now has all the logic in place:
我们现在可以回到我们添加后缀的方法,现在所有的逻辑都已经到位。
private void addSuffix(String suffix, int position) {
List<Node> nodes = getAllNodesInTraversePath(suffix, root, true);
if (nodes.size() == 0) {
addChildNode(root, suffix, position);
} else {
Node lastNode = nodes.remove(nodes.size() - 1);
String newText = suffix;
if (nodes.size() > 0) {
String existingSuffixUptoLastNode = nodes.stream()
.map(a -> a.getText())
.reduce("", String::concat);
newText = newText.substring(existingSuffixUptoLastNode.length());
}
extendNode(lastNode, newText, position);
}
}Finally, let’s modify our SuffixTree constructor to generate the suffixes and call our previous method addSuffix to add them iteratively to our data structure:
最后,让我们修改我们的SuffixTree构造函数来生成后缀,并调用我们之前的方法addSuffix来将它们迭加到我们的数据结构中。
public void SuffixTree(String text) {
root = new Node("", POSITION_UNDEFINED);
for (int i = 0; i < text.length(); i++) {
addSuffix(text.substring(i) + WORD_TERMINATION, i);
}
fullText = text;
}7.2. Searching Data
7.2.搜索数据
Having defined our suffix tree structure to store data, we can now write the logic for performing our search.
在定义了存储数据的后缀树结构后,我们现在可以编写执行搜索的逻辑。
We begin by adding a new method searchText on the SuffixTree class, taking in the pattern to search as an input:
我们首先在SuffixTree类上添加一个新的方法searchText,把要搜索的pattern作为一个输入。
public List<String> searchText(String pattern) {
// ...
}Next, to check if the pattern exists in our suffix tree, we call our helper method getAllNodesInTraversePath with the flag set for exact matches only, unlike during the adding of data when we allowed partial matches:
接下来,为了检查模式是否存在于我们的后缀树中,我们调用我们的辅助方法getAllNodesInTraversePath,并设置了仅用于精确匹配的标志,与添加数据时允许部分匹配不同。
List<Node> nodes = getAllNodesInTraversePath(pattern, root, false);We then get the list of nodes that match our pattern. The last node in the list indicates the node up to which the pattern matched exactly. So, our next step will be to get all the leaf nodes originating from this last matching node and get the positions stored in these leaf nodes.
然后我们得到符合我们模式的节点的列表。列表中的最后一个节点表示与该模式完全匹配的节点。因此,我们的下一步将是获得所有从这个最后一个匹配节点开始的叶子节点,并获得存储在这些叶子节点中的位置。
Let’s create a separate method getPositions to do this. We’ll check if the given node stores the final portion of a suffix to decide if its position value needs to be returned. And, we’ll do this recursively for every child of the given node:
让我们创建一个单独的方法getPositions来做这个。我们将检查给定节点是否存储了后缀的最后部分,以决定是否需要返回其位置值。而且,我们将对给定节点的每个子节点进行递归处理。
private List<Integer> getPositions(Node node) {
List<Integer> positions = new ArrayList<>();
if (node.getText().endsWith(WORD_TERMINATION)) {
positions.add(node.getPosition());
}
for (int i = 0; i < node.getChildren().size(); i++) {
positions.addAll(getPositions(node.getChildren().get(i)));
}
return positions;
}Once we have the set of positions, the next step is to use it to mark the patterns on the text we stored in our suffix tree. The position value indicates where the suffix starts, and the length of the pattern indicates how many characters to offset from the starting point. Applying this logic, let’s create a simple utility method:
一旦我们有了位置集,下一步就是用它来标记我们存储在后缀树上的文本的模式。位置值表示后缀开始的位置,而模式的长度表示从起点偏移多少个字符。应用这个逻辑,让我们创建一个简单的实用方法。
private String markPatternInText(Integer startPosition, String pattern) {
String matchingTextLHS = fullText.substring(0, startPosition);
String matchingText = fullText.substring(startPosition, startPosition + pattern.length());
String matchingTextRHS = fullText.substring(startPosition + pattern.length());
return matchingTextLHS + "[" + matchingText + "]" + matchingTextRHS;
}Now, we have our supporting methods ready. Therefore, we can add them to our search method and complete the logic:
现在,我们已经准备好了我们的支持方法。因此,我们可以将它们添加到我们的搜索方法中并完成逻辑。
public List<String> searchText(String pattern) {
List<String> result = new ArrayList<>();
List<Node> nodes = getAllNodesInTraversePath(pattern, root, false);
if (nodes.size() > 0) {
Node lastNode = nodes.get(nodes.size() - 1);
if (lastNode != null) {
List<Integer> positions = getPositions(lastNode);
positions = positions.stream()
.sorted()
.collect(Collectors.toList());
positions.forEach(m -> result.add((markPatternInText(m, pattern))));
}
}
return result;
}8. Testing
8.测试
Now that we have our algorithm in place, let’s test it.
现在我们的算法已经到位,让我们来测试一下。
First, let’s store a text in our SuffixTree:
首先,让我们在我们的SuffixTree中存储一个文本。
SuffixTree suffixTree = new SuffixTree("havanabanana");
Next, let’s search for a valid pattern a:
接下来,让我们搜索一个有效的模式a。
List<String> matches = suffixTree.searchText("a");
matches.stream().forEach(m -> LOGGER.debug(m));Running the code gives us six matches as expected:
运行该代码后,如预期的那样,我们得到了六个匹配。
h[a]vanabanana
hav[a]nabanana
havan[a]banana
havanab[a]nana
havanaban[a]na
havanabanan[a]Next, let’s search for another valid pattern nab:
接下来,让我们寻找另一个有效模式nab。
List<String> matches = suffixTree.searchText("nab");
matches.stream().forEach(m -> LOGGER.debug(m));
Running the code gives us only one match as expected:
运行该代码后,如预期的那样,我们只得到了一个匹配。
hava[nab]ananaFinally, let’s search for an invalid pattern nag:
最后,让我们寻找一个无效的模式nag。
List<String> matches = suffixTree.searchText("nag");
matches.stream().forEach(m -> LOGGER.debug(m));Running the code gives us no results. We see that matches have to be exact and not partial.
运行该代码,我们没有得到任何结果。我们看到,匹配必须是精确的,而不是部分的。
Thus, our pattern search algorithm has been able to satisfy all the expectations we laid out at the beginning of this tutorial.
因此,我们的模式搜索算法已经能够满足我们在本教程开始时提出的所有期望。
9. Time Complexity
9.时间的复杂性
When constructing the suffix tree for a given text of length t, the time complexity is O(t).
当为长度为t的给定文本构建后缀树时,时间复杂性为O(t)。
Then, for searching a pattern of length p, the time complexity is O(p). Recollect that for a brute-force search, it was O(p*t). Thus, pattern searching becomes faster after pre-processing of the text.
那么,对于搜索一个长度为p的模式, 时间复杂度为O(p)。请记住,对于粗暴的搜索,它是O(p*t)。 因此,在对文本进行预处理后,模式搜索变得更快。
10. Conclusion
10.结语
In this article, we first understood the concepts of three data structures – trie, suffix trie, and suffix tree. We then saw how a suffix tree could be used to compactly store suffixes.
在这篇文章中,我们首先了解了三种数据结构的概念– trie、后缀 trie 和后缀树。然后我们看到后缀树如何被用来紧凑地存储后缀。
Later, we saw how to use a suffix tree to store data and perform a pattern search.
后来,我们看到如何使用后缀树来存储数据并进行模式搜索。
As always, the source code with tests is available over on GitHub.
一如既往,带有测试的源代码可在GitHub上获得,。