1. Introduction
1.绪论
In this tutorial, we’ll study the process of generating a power set of a given set in Java.
在本教程中,我们将学习在Java中生成一个给定集合的power set的过程。
As a quick reminder, for every set of size n, there is a power set of size 2n. We’ll learn how to get it using various techniques.
作为快速提醒,对于每个大小n的集合,都有一个大小2n的幂集。我们将学习如何使用各种技术来获得它。
2. Definition of a Power Set
2.幂集的定义
The power set of a given set S is the set of all subsets of S, including S itself and the empty set.
一个给定集合S的幂集是S的所有子集的集合,包括S本身和空集。
For example, for a given set:
例如,对于一个给定的集合。
{"APPLE", "ORANGE", "MANGO"}the power set is:
权力集是。
{
{},
{"APPLE"},
{"ORANGE"},
{"APPLE", "ORANGE"},
{"MANGO"},
{"APPLE", "MANGO"},
{"ORANGE", "MANGO"},
{"APPLE", "ORANGE", "MANGO"}
}As it is also a set of subsets, the order of its internal subsets is not important and they can appear in any order:
由于它也是一个子集的集合,其内部子集的顺序并不重要,它们可以以任何顺序出现。
{
{},
{"MANGO"},
{"ORANGE"},
{"ORANGE", "MANGO"},
{"APPLE"},
{"APPLE", "MANGO"},
{"APPLE", "ORANGE"},
{"APPLE", "ORANGE", "MANGO"}
}3. Guava Library
3.番石榴图书馆
The Google Guava library has some useful Set utilities, such as the power set. Thus, we can easily use it to get the power set of the given set, too:
Google的Guava库有一些有用的Set工具,例如幂集。因此,我们也可以很容易地利用它来获得给定集合的幂集。
@Test
public void givenSet_WhenGuavaLibraryGeneratePowerSet_ThenItContainsAllSubsets() {
ImmutableSet<String> set = ImmutableSet.of("APPLE", "ORANGE", "MANGO");
Set<Set<String>> powerSet = Sets.powerSet(set);
Assertions.assertEquals((1 << set.size()), powerSet.size());
MatcherAssert.assertThat(powerSet, Matchers.containsInAnyOrder(
ImmutableSet.of(),
ImmutableSet.of("APPLE"),
ImmutableSet.of("ORANGE"),
ImmutableSet.of("APPLE", "ORANGE"),
ImmutableSet.of("MANGO"),
ImmutableSet.of("APPLE", "MANGO"),
ImmutableSet.of("ORANGE", "MANGO"),
ImmutableSet.of("APPLE", "ORANGE", "MANGO")
));
}Guava powerSet internally operates over the Iterator interface in the way when the next subset is requested, the subset is calculated and returned. So, the space complexity is reduced to O(n) instead of O(2n).
Guava powerSet在内部操作了Iterator接口,当请求下一个子集时,子集被计算并返回。因此,空间复杂度降低到了O(n)而不是O(2n)。
But, how does Guava achieve this?
但是,Guava是如何实现这一目标的?
4. Power Set Generation Approach
4.电力机组发电方式
4.1. Algorithm
4.1.算法
Let’s now discuss the possible steps for creating an algorithm for this operation.
现在让我们讨论一下为这一操作创建一个算法的可能步骤。
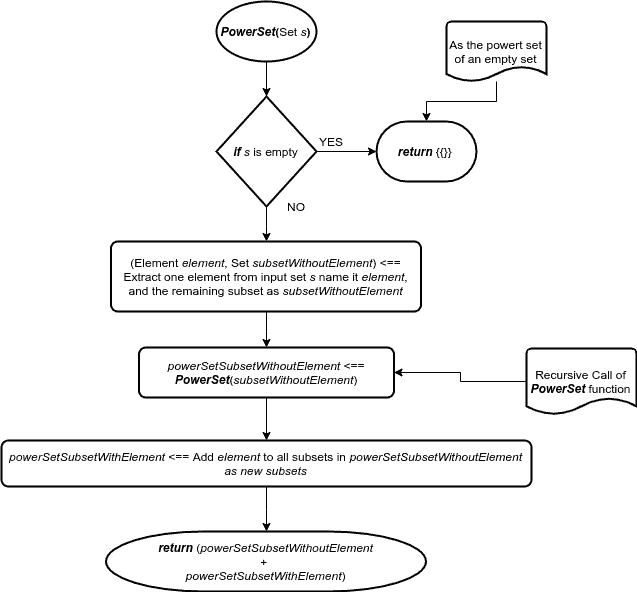
The power set of an empty set is {{}} in which it contains only one empty set, so that’s our simplest case.
空集的幂集是 {{}},其中只包含一个空集,所以这就是我们最简单的情况。
For every set S other than the empty set, we first extract one element and name it – element. Then, for the rest of the elements of a set subsetWithoutElement, we calculate their power set recursively – and name it something like powerSetSubsetWithoutElement. Then, by adding the extracted element to all sets in powerSetSubsetWithoutElement, we get powerSetSubsetWithElement.
对于除空集以外的每个集合S,我们首先提取一个元素并命名为–element。然后,对于集合subsetWithoutElement的其余元素,我们递归地计算它们的幂集–并命名为类似powerSetSubsetWithoutElement。然后,通过将提取的元素添加到powerSetSsubsetWithoutElement中的所有集合,我们得到powerSetSsubsetWithElement.。
Now, the power set S is the union of a powerSetSubsetWithoutElement and a powerSetSubsetWithElement:
现在,幂集S是powerSetSubsetWithoutElement和powerSetSubsetWithElement的联合。
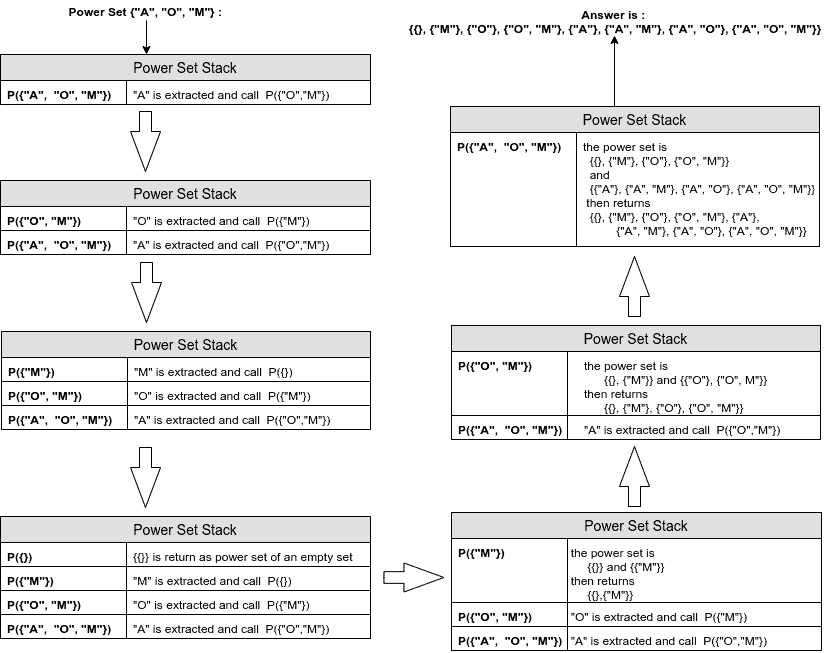
Let’s see an example of the recursive power set stack for the given set {“APPLE”, “ORANGE”, “MANGO”}.
让我们看看给定集合{“APPLE”, “ORANGE”, “MANGO”}的递归幂集栈的例子。
To improve the readability of the image we use short forms of names: P means power set function and “A”, “O”, “M” are short forms of “APPLE”, “ORANGE”, and “MANGO”, respectively:
为了提高图像的可读性,我们使用了名称的缩写形式。P表示幂集函数,“A”、”O”、”M”分别是“APPLE”、”ORANGE”和“MANGO”的缩写。
4.2. Implementation
4.2.实施
So, first, let’s write the Java code for extracting one element and get the remaining subsets:
所以,首先,让我们写出提取一个元素的Java代码,并得到剩余的子集。
T element = set.iterator().next();
Set<T> subsetWithoutElement = new HashSet<>();
for (T s : set) {
if (!s.equals(element)) {
subsetWithoutElement.add(s);
}
}We’ll then want to get the powerset of subsetWithoutElement:
然后我们要得到subsetWithoutElement的权力集。
Set<Set<T>> powersetSubSetWithoutElement = recursivePowerSet(subsetWithoutElement);Next, we need to add that powerset back into the original:
接下来,我们需要将该权力集添加到原版中。
Set<Set<T>> powersetSubSetWithElement = new HashSet<>();
for (Set<T> subsetWithoutElement : powerSetSubSetWithoutElement) {
Set<T> subsetWithElement = new HashSet<>(subsetWithoutElement);
subsetWithElement.add(element);
powerSetSubSetWithElement.add(subsetWithElement);
}Finally the union of powerSetSubSetWithoutElement and powerSetSubSetWithElement is the power set of the given input set:
最后,powerSetSubSetWithoutElement和powerSetSubSetWithElement的联合就是给定输入集的幂集。
Set<Set<T>> powerSet = new HashSet<>();
powerSet.addAll(powerSetSubSetWithoutElement);
powerSet.addAll(powerSetSubSetWithElement);If we put all our code snippets together, we can see our final product:
如果我们把所有的代码片段放在一起,我们就可以看到我们的最终产品。
public Set<Set<T>> recursivePowerSet(Set<T> set) {
if (set.isEmpty()) {
Set<Set<T>> ret = new HashSet<>();
ret.add(set);
return ret;
}
T element = set.iterator().next();
Set<T> subSetWithoutElement = getSubSetWithoutElement(set, element);
Set<Set<T>> powerSetSubSetWithoutElement = recursivePowerSet(subSetWithoutElement);
Set<Set<T>> powerSetSubSetWithElement = addElementToAll(powerSetSubSetWithoutElement, element);
Set<Set<T>> powerSet = new HashSet<>();
powerSet.addAll(powerSetSubSetWithoutElement);
powerSet.addAll(powerSetSubSetWithElement);
return powerSet;
}
4.3. Notes for Unit Tests
4.3.单元测试的注意事项
Now let’s test. We’ve got a bit of criteria here to confirm:
现在我们来测试一下。我们在这里有一点标准要确认。
- First, we check the size of the power set and it must be 2n for a set of size n.
- Then, every element will occur only one time in a subset and 2n-1 different subsets.
- Finally, every subset must appear once.
If all these conditions passed, we can be sure that our function works. Now, since we’ve used Set<Set>, we already know that there’s no repetition. In that case, we only need to check the size of the power set, and the number of occurrences of each element in the subsets.
如果所有这些条件都通过了,我们可以确定我们的函数是有效的。现在,由于我们已经使用了Set<Set>,我们已经知道不存在重复。在这种情况下,我们只需要检查幂集的大小,以及每个元素在子集中出现的次数。
To check the size of the power set we can use:
为了检查功率集的大小,我们可以使用。
MatcherAssert.assertThat(powerSet, IsCollectionWithSize.hasSize((1 << set.size())));And to check the number of occurrences of each element:
并检查每个元素的出现次数。
Map<String, Integer> counter = new HashMap<>();
for (Set<String> subset : powerSet) {
for (String name : subset) {
int num = counter.getOrDefault(name, 0);
counter.put(name, num + 1);
}
}
counter.forEach((k, v) -> Assertions.assertEquals((1 << (set.size() - 1)), v.intValue()));Finally, if we can put all together into one unit test:
最后,如果我们能把所有的东西放在一起,变成一个单元测试。
@Test
public void givenSet_WhenPowerSetIsCalculated_ThenItContainsAllSubsets() {
Set<String> set = RandomSetOfStringGenerator.generateRandomSet();
Set<Set<String>> powerSet = new PowerSet<String>().recursivePowerSet(set);
MatcherAssert.assertThat(powerSet, IsCollectionWithSize.hasSize((1 << set.size())));
Map<String, Integer> counter = new HashMap<>();
for (Set<String> subset : powerSet) {
for (String name : subset) {
int num = counter.getOrDefault(name, 0);
counter.put(name, num + 1);
}
}
counter.forEach((k, v) -> Assertions.assertEquals((1 << (set.size() - 1)), v.intValue()));
}5. Optimization
5.优化
In this section, we’ll try to minimize the space and reduce the number of internal operations to calculate the power set in an optimal way.
在本节中,我们将尝试最小化空间,减少内部操作的数量,以最佳方式计算幂集。
5.1. Data Structure
5.1.数据结构
As we can see in the given approach, we need a lot of subtractions in the recursive call, which consumes a large amount of time and memory.
正如我们在给定的方法中所看到的,我们需要在递归调用中进行大量的减法,这将消耗大量的时间和内存。
Instead, we can map each set or subset to some other notions to reduce the number of operations.
相反,我们可以将每个集合或子集映射到其他一些概念,以减少操作的数量。
First, we need to assign an increasing number starting from 0 to each object in the given set S which means we work with an ordered list of numbers.
首先,我们需要给给定集合S中的每个对象分配一个从0开始的递增数,这意味着我们要处理一个有序的数字列表。
For example for the given set {“APPLE”, “ORANGE”, “MANGO”} we get:
例如,对于给定的集合{“APPLE”, “ORANGE”, “MANGO”}我们得到。
“APPLE” -> 0
“APPLE” -> 0
“ORANGE” -> 1
“ORANGE” -> 1
“MANGO” -> 2
“MANGO” -> 2
So, from now on, instead of generating subsets of S, we generate them for the ordered list of [0, 1, 2], and as it is ordered we can simulate subtractions by a starting index.
所以,从现在开始,我们不再生成S的子集,而是为[0,1,2]的有序列表生成子集,由于它是有序的,我们可以通过一个起始索引来模拟减法的情况。
For example, if the starting index is 1 it means that we generate the power set of [1,2].
例如,如果起始指数是1,就意味着我们生成了[1,2]的幂集。
To retrieve mapped id from the object and vice-versa, we store both sides of mapping. Using our example, we store both (“MANGO” -> 2) and (2 -> “MANGO”). As the mapping of numbers started from zero, so for the reverse map there we can use a simple array to retrieve the respective object.
为了从对象中检索映射的id,反之亦然,我们要存储映射的两边。使用我们的例子,我们同时存储(“MANGO” -> 2)和(2 -> “MANGO”)。由于数字的映射是从零开始的,所以对于反向映射,我们可以使用一个简单的数组来检索各自的对象。
One of the possible implementations of this function would be:
这个函数的一个可能的实现方式是。
private Map<T, Integer> map = new HashMap<>();
private List<T> reverseMap = new ArrayList<>();
private void initializeMap(Collection<T> collection) {
int mapId = 0;
for (T c : collection) {
map.put(c, mapId++);
reverseMap.add(c);
}
}Now, to represent subsets there are two well-known ideas:
现在,为了表示子集,有两个著名的想法。
- Index representation
- Binary representation
5.2. Index Representation
5.2.索引表示法
Each subset is represented by the index of its values. For example, the index mapping of the given set {“APPLE”, “ORANGE”, “MANGO”} would be:
每个子集都由其值的索引来表示。例如,给定集合的索引映射 {“APPLE”, “ORANGE”, “MANGO”}将是。
{
{} -> {}
[0] -> {"APPLE"}
[1] -> {"ORANGE"}
[0,1] -> {"APPLE", "ORANGE"}
[2] -> {"MANGO"}
[0,2] -> {"APPLE", "MANGO"}
[1,2] -> {"ORANGE", "MANGO"}
[0,1,2] -> {"APPLE", "ORANGE", "MANGO"}
}So, we can retrieve the respective set from a subset of indices with the given mapping:
因此,我们可以通过给定的映射从索引的子集中检索出相应的集合。
private Set<Set<T>> unMapIndex(Set<Set<Integer>> sets) {
Set<Set<T>> ret = new HashSet<>();
for (Set<Integer> s : sets) {
HashSet<T> subset = new HashSet<>();
for (Integer i : s) {
subset.add(reverseMap.get(i));
}
ret.add(subset);
}
return ret;
}5.3. Binary Representation
5.3.二进制表示法
Or, we can represent each subset using binary. If an element of the actual set exists in this subset its respective value is 1; otherwise it is 0.
或者,我们可以用二进制来表示每个子集。如果实际集合中的一个元素存在于这个子集中,其各自的值就是1;否则就是0。
For our fruit example, the power set would be:
对于我们的水果例子,动力组将是。
{
[0,0,0] -> {}
[1,0,0] -> {"APPLE"}
[0,1,0] -> {"ORANGE"}
[1,1,0] -> {"APPLE", "ORANGE"}
[0,0,1] -> {"MANGO"}
[1,0,1] -> {"APPLE", "MANGO"}
[0,1,1] -> {"ORANGE", "MANGO"}
[1,1,1] -> {"APPLE", "ORANGE", "MANGO"}
}So, we can retrieve the respective set from a binary subset with the given mapping:
因此,我们可以通过给定的映射从二进制子集中检索出相应的集合。
private Set<Set<T>> unMapBinary(Collection<List<Boolean>> sets) {
Set<Set<T>> ret = new HashSet<>();
for (List<Boolean> s : sets) {
HashSet<T> subset = new HashSet<>();
for (int i = 0; i < s.size(); i++) {
if (s.get(i)) {
subset.add(reverseMap.get(i));
}
}
ret.add(subset);
}
return ret;
}5.4. Recursive Algorithm Implementation
5.4.递归算法的实现
In this step, we’ll try to implement the previous code using both data structures.
在这一步,我们将尝试使用这两种数据结构来实现前面的代码。
Before calling one of these functions, we need to call the initializeMap method to get the ordered list. Also, after creating our data structure, we need to call the respective unMap function to retrieve the actual objects:
在调用这些函数之一之前,我们需要调用initializeMap方法来获得有序的列表。另外,在创建我们的数据结构后,我们需要调用相应的unMap函数来检索实际的对象。
public Set<Set<T>> recursivePowerSetIndexRepresentation(Collection<T> set) {
initializeMap(set);
Set<Set<Integer>> powerSetIndices = recursivePowerSetIndexRepresentation(0, set.size());
return unMapIndex(powerSetIndices);
}So, let’s try our hand at the index representation:
因此,让我们来尝试一下索引的表示方法。
private Set<Set<Integer>> recursivePowerSetIndexRepresentation(int idx, int n) {
if (idx == n) {
Set<Set<Integer>> empty = new HashSet<>();
empty.add(new HashSet<>());
return empty;
}
Set<Set<Integer>> powerSetSubset = recursivePowerSetIndexRepresentation(idx + 1, n);
Set<Set<Integer>> powerSet = new HashSet<>(powerSetSubset);
for (Set<Integer> s : powerSetSubset) {
HashSet<Integer> subSetIdxInclusive = new HashSet<>(s);
subSetIdxInclusive.add(idx);
powerSet.add(subSetIdxInclusive);
}
return powerSet;
}Now, let’s see the binary approach:
现在,让我们看看二进制方法。
private Set<List<Boolean>> recursivePowerSetBinaryRepresentation(int idx, int n) {
if (idx == n) {
Set<List<Boolean>> powerSetOfEmptySet = new HashSet<>();
powerSetOfEmptySet.add(Arrays.asList(new Boolean[n]));
return powerSetOfEmptySet;
}
Set<List<Boolean>> powerSetSubset = recursivePowerSetBinaryRepresentation(idx + 1, n);
Set<List<Boolean>> powerSet = new HashSet<>();
for (List<Boolean> s : powerSetSubset) {
List<Boolean> subSetIdxExclusive = new ArrayList<>(s);
subSetIdxExclusive.set(idx, false);
powerSet.add(subSetIdxExclusive);
List<Boolean> subSetIdxInclusive = new ArrayList<>(s);
subSetIdxInclusive.set(idx, true);
powerSet.add(subSetIdxInclusive);
}
return powerSet;
}5.5. Iterate Through [0, 2n)
5.5.通过[0, 2n)进行迭代
Now, there is a nice optimization we can do with the binary representation. If we look at it, we can see that each row is equivalent to the binary format of a number in [0, 2n).
现在,我们可以对二进制表示法做一个很好的优化。如果我们看一下,我们可以看到每一行都相当于[0, 2n)中一个数字的二进制格式。
So, if we iterate through numbers from 0 to 2n, we can convert that index to binary, and use it to create a boolean representation of each subset:
因此,如果我们遍历从0到2n的数字,我们可以将该索引转换成二进制,并使用它来创建每个子集的布尔表示。
private List<List<Boolean>> iterativePowerSetByLoopOverNumbers(int n) {
List<List<Boolean>> powerSet = new ArrayList<>();
for (int i = 0; i < (1 << n); i++) {
List<Boolean> subset = new ArrayList<>(n);
for (int j = 0; j < n; j++)
subset.add(((1 << j) & i) > 0);
powerSet.add(subset);
}
return powerSet;
}5.6. Minimal Change Subsets by Gray Code
5.6.按灰色代码划分的最小变化子集
Now, if we define any bijective function from binary representation of length n to a number in [0, 2n), we can generate subsets in any order that we want.
现在,如果我们定义任何客观函数,从长度为n的二进制表示到[0, 2n)中的一个数字,我们可以按照我们想要的任何顺序产生子集。
Gray Code is a well-known function that is used to generate binary representations of numbers so that the binary representation of consecutive numbers differ by only one bit (even the difference of the last and first numbers is one).
灰色代码是一个著名的函数,用于生成数字的二进制表示,使连续的数字的二进制表示只相差一个比特(甚至最后一个和第一个数字的差别也是一个)。
We can thus optimize this just a bit further:
因此,我们可以进一步优化这一点。
private List<List<Boolean>> iterativePowerSetByLoopOverNumbersWithGrayCodeOrder(int n) {
List<List<Boolean>> powerSet = new ArrayList<>();
for (int i = 0; i < (1 << n); i++) {
List<Boolean> subset = new ArrayList<>(n);
for (int j = 0; j < n; j++) {
int grayEquivalent = i ^ (i >> 1);
subset.add(((1 << j) & grayEquivalent) > 0);
}
powerSet.add(subset);
}
return powerSet;
}6. Lazy Loading
6.懒惰的加载
To minimize the space usage of power set, which is O(2n), we can utilize the Iterator interface to fetch every subset, and also every element in each subset lazily.
为了最小化幂集的空间使用,即O(2n),我们可以利用Iterator接口来获取每个子集,以及每个子集中的每个元素。
6.1. ListIterator
6.1.ListIterator
First, to be able to iterate from 0 to 2n, we should have a special Iterator that loops over this range but not consuming the whole range beforehand.
首先,为了能够从0到2n进行迭代,我们应该有一个特殊的Iterator,在这个范围内循环,但不事先消耗整个范围。
To solve this problem, we’ll use two variables; one for the size, which is 2n, and another for the current subset index. Our hasNext() function will check that position is less than size:
为了解决这个问题,我们将使用两个变量;一个是大小,即2n,另一个是当前子集索引。我们的hasNext() 函数将检查position是否小于size:。
abstract class ListIterator<K> implements Iterator<K> {
protected int position = 0;
private int size;
public ListIterator(int size) {
this.size = size;
}
@Override
public boolean hasNext() {
return position < size;
}
}And our next() function returns the subset for the current position and increases the value of position by one:
而我们的next()函数返回当前位置的子集,并将位置的值增加1。
@Override
public Set<E> next() {
return new Subset<>(map, reverseMap, position++);
}6.2. Subset
6.2.子集
To have a lazy load Subset, we define a class that extends AbstractSet, and we override some of its functions.
为了拥有一个懒惰的加载Subset,我们定义了一个扩展AbstractSet的类,并覆盖了它的一些功能。
By looping over all bits that are 1 in the receiving mask (or position) of the Subset, we can implement the Iterator and other methods in AbstractSet.
通过在Subset的接收掩码(或位置)中的所有位上循环,我们可以实现Iterator和AbstractSet的其他方法。
For example, the size() is the number of 1s in the receiving mask:
例如,size()是接收mask中的1的数量。
@Override
public int size() {
return Integer.bitCount(mask);
}And the contains() function is just whether the respective bit in the mask is 1 or not:
而contains() 函数只是说明mask中的相应位是否是1。
@Override
public boolean contains(@Nullable Object o) {
Integer index = map.get(o);
return index != null && (mask & (1 << index)) != 0;
}We use another variable – remainingSetBits – to modify it whenever we retrieve its respective element in the subset we change that bit to 0. Then, the hasNext() checks if remainingSetBits is not zero (that is, it has at least one bit with a value of 1):
我们使用另一个变量–remainingSetBits–来修改它,每当我们在子集中检索到它各自的元素时,我们就把那个位改为0。然后,hasNext() 检查remainingSetBits 是否不为零(也就是说,它至少有一个比特的值为1)。
@Override
public boolean hasNext() {
return remainingSetBits != 0;
}And the next() function uses the right-most 1 in the remainingSetBits, then converts it to 0, and also returns the respective element:
而next()函数使用remainingSetBits中最右边的1,然后将其转换为0,并且还返回相应的元素。
@Override
public E next() {
int index = Integer.numberOfTrailingZeros(remainingSetBits);
if (index == 32) {
throw new NoSuchElementException();
}
remainingSetBits &= ~(1 << index);
return reverseMap.get(index);
}6.3. PowerSet
6.3.PowerSet
To have a lazy-load PowerSet class, we need a class that extends AbstractSet<Set<T>>.
为了拥有一个懒惰加载的PowerSet类,我们需要一个扩展AbstractSet<Set<T>>的类。
The size() function is simply 2 to the power of the set’s size:
size()函数是简单的2到集合大小的幂。
@Override
public int size() {
return (1 << this.set.size());
}As the power set will contain all possible subsets of the input set, so contains(Object o) function checks if all elements of the object o are existing in the reverseMap (or in the input set):
由于幂集将包含输入集的所有可能的子集,所以contains(Object o)函数检查object o的所有元素是否存在于reverseMap中(或输入集中)。
@Override
public boolean contains(@Nullable Object obj) {
if (obj instanceof Set) {
Set<?> set = (Set<?>) obj;
return reverseMap.containsAll(set);
}
return false;
}To check equality of a given Object with this class, we can only check if the input set is equal to the given Object:
要检查一个给定的Object与这个类的平等性,我们只能检查输入的set是否与给定的Object相等。
@Override
public boolean equals(@Nullable Object obj) {
if (obj instanceof PowerSet) {
PowerSet<?> that = (PowerSet<?>) obj;
return set.equals(that.set);
}
return super.equals(obj);
}The iterator() function returns an instance of ListIterator that we defined already:
iterator() 函数返回我们已经定义的ListIterator的一个实例。
@Override
public Iterator<Set<E>> iterator() {
return new ListIterator<Set<E>>(this.size()) {
@Override
public Set<E> next() {
return new Subset<>(map, reverseMap, position++);
}
};
}The Guava library uses this lazy-load idea and these PowerSet and Subset are the equivalent implementations of the Guava library.
Guava库使用了这种懒惰加载的思想,这些PowerSet和Subset是Guava库的等效实现。。
For more information, check their source code and documentation.
Furthermore, if we want to do parallel operation over subsets in PowerSet, we can call Subset for different values in a ThreadPool.
此外,如果我们想对PowerSet中的子集进行并行操作,我们可以针对ThreadPool中的不同值调用Subset。
7. Summary
7.摘要
To sum up, first, we studied what is a power set. Then, we generated it by using the Guava Library. After that, we studied the approach and how we should implement it, and also how to write a unit test for it.
总而言之,首先,我们研究了什么是幂集。然后,我们通过使用Guava库来生成它。之后,我们研究了方法和如何实现它,以及如何为它写一个单元测试。
Finally, we utilized the Iterator interface to optimize the space of generation of subsets and also their internal elements.
最后,我们利用迭代器接口来优化子集的生成空间,也优化其内部元素。
As always the source code is available over on GitHub.
像往常一样,源代码可在GitHub上获得超过。