1. Overview
1.概述
In this tutorial, we’ll learn how to compute the median of a stream of integers.
在本教程中,我们将学习如何计算一个整数流的中位数。
We’ll proceed by stating the problem with examples, then analyze the problem, and finally implement several solutions in Java.
我们将通过实例说明问题,然后分析问题,最后用Java实现几个解决方案。
2. Problem Statement
问题陈述
Median is the middle value of an ordered data set. For a set of integers, there are just as many elements less than the median as greater.
中位数是一个有序数据集的中间值。对于一组整数来说,小于中位数的元素和大于中位数的元素一样多。。
In an ordered set of:
在一个有序的集合中。
- odd number of integers, the middle element is the median – in the ordered set { 5, 7, 10 }, the median is 7
- even number of integers, there’s no middle element; the median is computed as the average of the two middle elements – in the ordered set {5, 7, 8, 10}, the median is (7 + 8) / 2 = 7.5
Now, let’s assume that instead of a finite set, we’re reading integers off a data stream. We can define the median of a stream of integers as the median of the set of integers read so far.
现在,让我们假设我们从数据流中读取的不是一个有限集,而是整数。我们可以把整数流的中位数定义为到目前为止所读取的整数集合的中位数。
Let’s formalize the problem statement. Given an input of a stream of integers, we must design a class that performs the following two tasks for each integer that we read:
让我们把问题陈述正式化。给定一个整数流的输入,我们必须设计一个类,为我们读取的每个整数执行以下两个任务。
- Add the integer to the set of integers
- Find the median of the integers read so far
For example:
比如说。
add 5 // sorted-set = { 5 }, size = 1
get median -> 5
add 7 // sorted-set = { 5, 7 }, size = 2
get median -> (5 + 7) / 2 = 6
add 10 // sorted-set = { 5, 7, 10 }, size = 3
get median -> 7
add 8 // sorted-set = { 5, 7, 8, 10 }, size = 4
get median -> (7 + 8) / 2 = 7.5
..
Although the stream is non-finite, we can assume that we can hold all the elements of the stream in memory at once.
虽然流是非无限的,但我们可以假设我们可以在内存中同时容纳流的所有元素。
We can represent our tasks as the following operations in code:
我们可以在代码中把我们的任务表述为以下操作。
void add(int num);
double getMedian();
3. Naive Approach
3.天真的方法
3.1. Sorted List
3.1.排序的列表
Let’s begin with a simple idea – we can compute the median of a sorted list of integers by accessing the middle element or the middle two elements of the list, by index. The time complexity of the getMedian operation is O(1).
让我们从一个简单的想法开始–我们可以通过访问列表中的中间元素或中间的两个元素,通过索引来计算一个排序的列表的中位数。getMedian操作的时间复杂性为O(1)。
While adding a new integer, we must determine its correct position in the list such that the list remains sorted. This operation can be performed in O(n) time, where n is the size of the list. So, the overall cost of adding a new element to the list and computing the new median is O(n).
在添加一个新的整数时,我们必须确定它在列表中的正确位置,从而使列表保持排序。这个操作可以在O(n)时间内完成,其中n是列表的大小。所以,向列表添加新元素和计算新中位数的总成本是O(n)。
3.2. Improving on the Naive Approach
3.2.对天真的方法进行改进
The add operation runs in linear time, which isn’t optimal. Let’s try to address that in this section.
添加操作在线性时间内运行,这并不是最佳状态。让我们在本节中尝试解决这个问题。
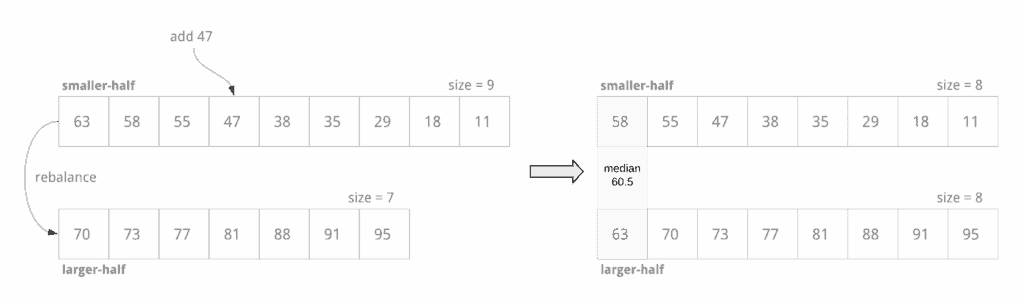
We can split the list into two sorted lists – the smaller half of the integers sorted in decreasing order, and the larger half of the integers in increasing order. We can add a new integer into the appropriate half such that the size of the lists differs by 1, at most:
我们可以将列表分成两个排序的列表—小半数的整数按递减顺序排序,大半数的整数按递增顺序排序。我们可以在相应的一半中添加一个新的整数,使列表的大小最多相差1。
if element is smaller than min. element of larger half:
insert into smaller half at appropriate index
if smaller half is much bigger than larger half:
remove max. element of smaller half and insert at the beginning of larger half (rebalance)
else
insert into larger half at appropriate index:
if larger half is much bigger than smaller half:
remove min. element of larger half and insert at the beginning of smaller half (rebalance)
Now, we can compute the median:
现在,我们可以计算出中位数。
if lists contain equal number of elements:
median = (max. element of smaller half + min. element of larger half) / 2
else if smaller half contains more elements:
median = max. element of smaller half
else if larger half contains more elements:
median = min. element of larger halfThough we have only improved the time complexity of the add operation by some constant factor, we have made progress.
尽管我们只是将add操作的时间复杂度提高了一些常数,但我们已经取得了进展。
Let’s analyze the elements we access in the two sorted lists. We potentially access each element as we shift them during the (sorted) add operation. More importantly, we access the minimum and maximum (extremums) of the larger and smaller halves respectively, during the add operation for rebalancing and during the getMedian operation.
让我们分析一下我们在两个排序的列表中访问的元素。在(排序的)add操作过程中,我们可能会访问每个元素,因为我们会对它们进行移动。更重要的是,我们在add 操作期间和getMedian 操作期间,分别访问大半和小半的最小和最大(极值),以便进行再平衡。
We can see that extremums are the first elements of their respective lists. So, we must optimize for accessing the element at index 0 for each half to improve the overall running time of the add operation.
我们可以看到,extremums是其各自列表的第一个元素。所以,我们必须优化访问每个半数的索引0的元素,以改善add操作的整体运行时间。
4. Heap-based Approach
4.基于堆的方法
Let’s refine our understanding of the problem, by applying what we’ve learned from our naive approach:
让我们通过应用我们从天真的方法中学到的东西来完善我们对这个问题的理解。
- We must get the minimum/maximum element of a dataset in O(1) time
- The elements don’t have to be kept in a sorted order as long as we can get the minimum/maximum element efficiently
- We need to find an approach for adding an element to our dataset that costs less than O(n) time
Next, we’ll look at the Heap data structure that helps us achieve our goals efficiently.
接下来,我们将看看帮助我们有效实现目标的Heap数据结构。
4.1. Heap Data Structure
4.1.堆数据结构
Heap is a data structure that is usually implemented with an array but can be thought of as a binary tree.
Heap是一种数据结构,通常用数组实现,但也可以认为是二叉树。
Heaps are constrained by the heap property:
堆是由堆的属性来制约的。
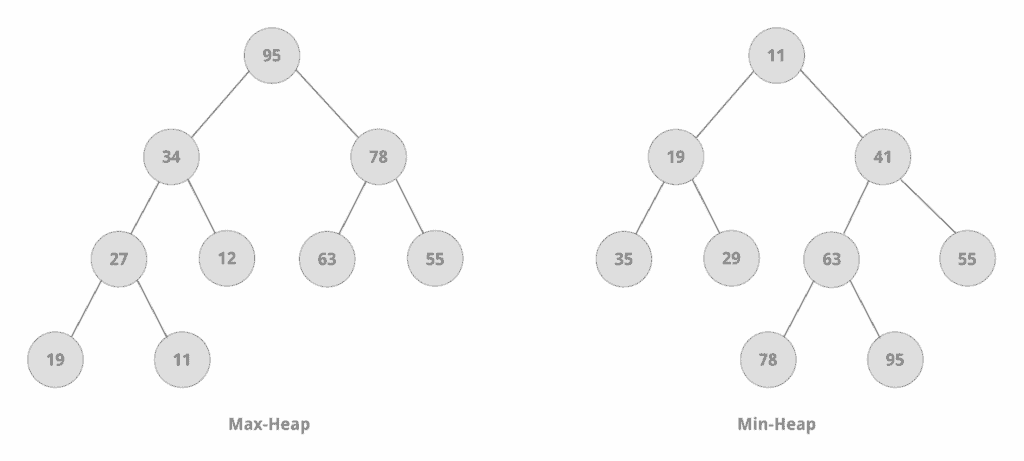
4.1.1. Max–heap Property
A (child) node can’t have a value greater than that of its parent. Hence, in a max-heap, the root node always has the largest value.
一个(子)节点的值不能大于其父节点的值。因此,在一个最大堆中,根节点总是有最大的值。
4.1.2. Min–heap Property
A (parent) node can’t have a value greater than that of its children. Thus, in a min-heap, the root node always has the smallest value.
一个(父)节点的值不能大于其子节点的值。因此,在一个min-heap中,根节点总是有最小的值。
In Java, the PriorityQueue class represents a heap. Let’s move ahead to our first solution using heaps.
在Java中,PriorityQueue类代表一个堆。让我们前进到我们的第一个使用堆的解决方案。
4.2. First Solution
4.2.第一个解决方案
Let’s replace the lists in our naive approach with two heaps:
让我们用两个堆来代替我们天真的方法中的列表。
- A min-heap that contains the larger half of the elements, with the minimum element at the root
- A max-heap that contains the smaller half of the elements, with the maximum element at the root
Now, we can add the incoming integer to the relevant half by comparing it with the root of the min-heap. Next, if after insertion, the size of one heap differs from that of the other heap by more than 1, we can rebalance the heaps, thus maintaining a size difference of at most 1:
现在,我们可以通过与最小堆的根进行比较,将传入的整数添加到相关的一半。接下来,如果在插入后,一个堆的大小与另一个堆的大小相差超过1,我们可以重新平衡这些堆,从而保持最多1的大小差异。
if size(minHeap) > size(maxHeap) + 1:
remove root element of minHeap, insert into maxHeap
if size(maxHeap) > size(minHeap) + 1:
remove root element of maxHeap, insert into minHeapWith this approach, we can compute the median as the average of the root elements of both the heaps, if the size of the two heaps is equal. Otherwise, the root element of the heap with more elements is the median.
通过这种方法,如果两个堆的大小相等,我们可以将中位数计算为两个堆的根元素的平均值。否则,有更多元素的堆的根元素就是中位数。
We’ll use the PriorityQueue class to represent the heaps. The default heap property of a PriorityQueue is min-heap. We can create a max-heap by using a Comparator.reverserOrder that uses the reverse of the natural order:
我们将使用PriorityQueue类来表示堆。PriorityQueue的默认堆属性是min-heap。我们可以通过使用Comparator.reverserOrder来创建一个最大堆,它使用的是自然顺序的反向。
class MedianOfIntegerStream {
private Queue<Integer> minHeap, maxHeap;
MedianOfIntegerStream() {
minHeap = new PriorityQueue<>();
maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
}
void add(int num) {
if (!minHeap.isEmpty() && num < minHeap.peek()) {
maxHeap.offer(num);
if (maxHeap.size() > minHeap.size() + 1) {
minHeap.offer(maxHeap.poll());
}
} else {
minHeap.offer(num);
if (minHeap.size() > maxHeap.size() + 1) {
maxHeap.offer(minHeap.poll());
}
}
}
double getMedian() {
int median;
if (minHeap.size() < maxHeap.size()) {
median = maxHeap.peek();
} else if (minHeap.size() > maxHeap.size()) {
median = minHeap.peek();
} else {
median = (minHeap.peek() + maxHeap.peek()) / 2;
}
return median;
}
}Before we analyze the running time of our code, let’s look at the time complexity of the heap operations we have used:
在分析我们代码的运行时间之前,让我们看看我们所使用的堆操作的时间复杂性。
find-min/find-max O(1)
delete-min/delete-max O(log n)
insert O(log n)
So, the getMedian operation can be performed in O(1) time as it requires the find-min and find-max functions only. The time complexity of the add operation is O(log n) – three insert/delete calls each requiring O(log n) time.
因此,getMedian操作可以在O(1)时间内执行,因为它只需要find-min和find-max函数。添加操作的时间复杂度是O(log n)–三个插入/删除调用,每个调用需要O(log n)时间。
4.3. Heap Size Invariant Solution
4.3.堆大小不变的解决方案
In our previous approach, we compared each new element with the root elements of the heaps. Let’s explore another approach using heap in which we can leverage the heap property to add a new element in the appropriate half.
在我们之前的方法中,我们将每个新元素与堆的根元素进行比较。让我们探索另一种使用堆的方法,在这种方法中,我们可以利用堆的属性,在适当的一半中添加一个新元素。
As we have done for our previous solution, we begin with two heaps – a min-heap and a max-heap. Next, let’s introduce a condition: the size of the max-heap must be (n / 2) at all times, while the size of the min-heap can be either (n / 2) or (n / 2) + 1, depending on the total number of elements in the two heaps. In other words, we can allow only the min-heap to have an extra element, when the total number of elements is odd.
就像我们之前的解决方案一样,我们从两个堆开始–一个最小堆和一个最大堆。接下来,让我们引入一个条件。最大堆的大小在任何时候都必须是(n / 2),而最小堆的大小可以是(n / 2)或(n / 2) + 1,取决于两个堆中元素的总数。换句话说,当元素总数为奇数时,我们可以只允许最小堆有一个额外的元素。
With our heap size invariant, we can compute the median as the average of the root elements of both heaps, if the sizes of both heaps are (n / 2). Otherwise, the root element of the min-heap is the median.
有了我们的堆大小不变性,如果两个堆的大小都是(n / 2),我们可以将中位数计算为两个堆的根元素的平均值。否则,最小堆的根元素就是中位数。
When we add a new integer, we have two scenarios:
当我们添加一个新的整数时,我们有两种情况。
1. Total no. of existing elements is even
size(min-heap) == size(max-heap) == (n / 2)
2. Total no. of existing elements is odd
size(max-heap) == (n / 2)
size(min-heap) == (n / 2) + 1
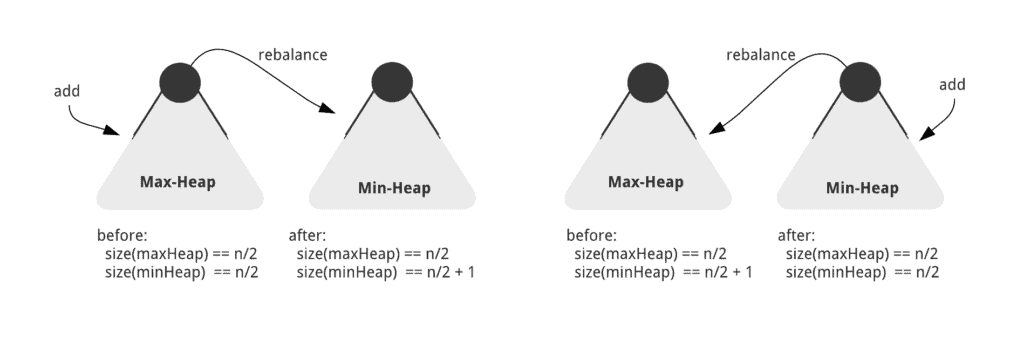
We can maintain the invariant by adding the new element to one of the heaps and rebalancing every time:
我们可以通过将新元素添加到其中一个堆中并每次重新平衡来维持这个不变性。
The rebalancing works by moving the largest element from the max-heap to the min-heap, or by moving the smallest element from the min-heap to the max-heap. This way, though we’re not comparing the new integer before adding it to a heap, the subsequent rebalancing ensures that we honor the underlying invariant of smaller and larger halves.
重新平衡的工作方式是将最大的元素从最大堆移到最小堆,或者将最小的元素从最小堆移到最大堆。这样,尽管我们在将新的整数添加到堆之前没有进行比较,但随后的再平衡确保我们尊重小半和大半的基本不变性。
Let’s implement our solution in Java using PriorityQueues:
让我们在Java中使用PriorityQueues来实现我们的解决方案。
class MedianOfIntegerStream {
private Queue<Integer> minHeap, maxHeap;
MedianOfIntegerStream() {
minHeap = new PriorityQueue<>();
maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
}
void add(int num) {
if (minHeap.size() == maxHeap.size()) {
maxHeap.offer(num);
minHeap.offer(maxHeap.poll());
} else {
minHeap.offer(num);
maxHeap.offer(minHeap.poll());
}
}
double getMedian() {
int median;
if (minHeap.size() > maxHeap.size()) {
median = minHeap.peek();
} else {
median = (minHeap.peek() + maxHeap.peek()) / 2;
}
return median;
}
}The time complexities of our operations remain unchanged: getMedian costs O(1) time, while add runs in time O(log n) with exactly the same number of operations.
我们操作的时间复杂度保持不变。getMedian花费了O(1)时间,而add的运行时间O(log n),操作数量完全相同。
Both the heap-based solutions offer similar space and time complexities. While the second solution is clever and has a cleaner implementation, the approach isn’t intuitive. On the other hand, the first solution follows our intuition naturally, and it’s easier to reason about the correctness of its add operation.
两种基于堆的解决方案都提供了类似的空间和时间的复杂性。虽然第二个解决方案很聪明,而且有一个更干净的实现,但这个方法并不直观。另一方面,第一个解决方案自然地遵循我们的直觉,而且更容易推理出其add操作的正确性。
5. Conclusion
5.结论
In this tutorial, we learned how to compute the median of a stream of integers. We evaluated a few approaches and implemented a couple of different solutions in Java using PriorityQueue.
在本教程中,我们学习了如何计算一个整数流的中位数。我们评估了几种方法,并使用PriorityQueue在Java中实现了几种不同的解决方案。
As usual, the source code for all the examples is available over on GitHub.
像往常一样,所有例子的源代码都可以在GitHub上找到。