1. Overview
1.概述
Most of the time, when we’re implementing graph-based algorithms, we also need to implement some utility functions.
大多数时候,当我们实现基于图的算法时,我们也需要实现一些效用函数。
JGraphT is an open-source Java class library which not only provides us with various types of graphs but also many useful algorithms for solving most frequently encountered graph problems.
JGraphT是一个开源的Java类库,它不仅为我们提供了各种类型的图,还提供了许多有用的算法来解决最常遇到的图问题。
In this article, we’ll see how to create different types of graphs and how convenient it is to use the provided utilities.
在这篇文章中,我们将看到如何创建不同类型的图表,以及使用所提供的工具有多方便。
2. Maven Dependency
2.Maven的依赖性
Let’s start by adding the dependency to our Maven project:
我们先把依赖关系添加到我们的Maven项目中。
<dependency>
<groupId>org.jgrapht</groupId>
<artifactId>jgrapht-core</artifactId>
<version>1.0.1</version>
</dependency>The latest version can be found at the Maven Central.
最新版本可在Maven中心找到。
3. Creating Graphs
3.创建图表
JGraphT supports various types of graphs.
JGraphT支持各种类型的图。
3.1. Simple Graphs
3.1.简单图形
For starters, let’s create a simple graph with a vertex of type String:
首先,让我们创建一个简单的图,其顶点类型为String。
Graph<String, DefaultEdge> g
= new SimpleGraph<>(DefaultEdge.class);
g.addVertex(“v1”);
g.addVertex(“v2”);
g.addEdge(v1, v2);3.2. Directed/Undirected Graphs
3.2.有向/无向图
It also allows us to create directed/undirected graphs.
它还允许我们创建有向/无向图。
In our example, we’ll create a directed graph and use it to demonstrate other utility functions and algorithms:
在我们的例子中,我们将创建一个有向图,并使用它来演示其他实用功能和算法。
DirectedGraph<String, DefaultEdge> directedGraph
= new DefaultDirectedGraph<>(DefaultEdge.class);
directedGraph.addVertex("v1");
directedGraph.addVertex("v2");
directedGraph.addVertex("v3");
directedGraph.addEdge("v1", "v2");
// Add remaining vertices and edges3.3. Complete Graphs
3.3.完整的图形
Similarly, we can also generate a complete graph:
同样地,我们也可以生成一个完整的图。
public void createCompleteGraph() {
completeGraph = new SimpleWeightedGraph<>(DefaultEdge.class);
CompleteGraphGenerator<String, DefaultEdge> completeGenerator
= new CompleteGraphGenerator<>(size);
VertexFactory<String> vFactory = new VertexFactory<String>() {
private int id = 0;
public String createVertex() {
return "v" + id++;
}
};
completeGenerator.generateGraph(completeGraph, vFactory, null);
}3.4. Multi-Graphs
3.4.多重图形
Other than simple-graphs, API also provides us with multigraphs (graphs with multiple paths between two vertices).
除了简单图之外,API还为我们提供了多图(两个顶点之间有多条路径的图)。
Besides, we can have weighted/unweighted or user-defined edges in any graph.
此外,我们可以在任何图中拥有加权/非加权或用户定义的边。
Let’s create a multigraph with weighted edges:
让我们创建一个有加权边的多图。
public void createMultiGraphWithWeightedEdges() {
multiGraph = new Multigraph<>(DefaultWeightedEdge.class);
multiGraph.addVertex("v1");
multiGraph.addVertex("v2");
DefaultWeightedEdge edge1 = multiGraph.addEdge("v1", "v2");
multiGraph.setEdgeWeight(edge1, 5);
DefaultWeightedEdge edge2 = multiGraph.addEdge("v1", "v2");
multiGraph.setEdgeWeight(edge2, 3);
}In addition to this, we can have unmodifiable (read-only) and listenable (allows external listeners to track modifications) graphs as well as subgraphs. Also, we can always create all compositions of these graphs.
除此之外,我们可以有不可修改(只读)和可监听(允许外部监听者跟踪修改)的图以及子图。另外,我们还可以随时创建这些图的所有组合。
Further API details can be found here.
进一步的API细节可以在这里找到。
4. API Algorithms
4.API算法
Now, that we’ve got full fledge graph objects, let’s look at some common problems and their solutions.
现在,我们已经有了完整的图形对象,让我们来看看一些常见的问题和它们的解决方案。
4.1. Graph Iteration
4.1.图形迭代
We can traverse the graph using various iterators such as BreadthFirstIterator, DepthFirstIterator, ClosestFirstIterator, RandomWalkIterator as per the requirement.
We simply need to create an instance of respective iterators by passing graph objects:
我们可以使用各种迭代器来遍历图形,如BreadthFirstIterator、DepthFirstIterator、ClosestFirstIterator、RandomWalkIterator,以满足要求。
我们只需要通过传递图形对象来创建各自迭代器的实例。
DepthFirstIterator depthFirstIterator
= new DepthFirstIterator<>(directedGraph);
BreadthFirstIterator breadthFirstIterator
= new BreadthFirstIterator<>(directedGraph);Once we get the iterator objects, we can perform the iteration using hasNext() and next() methods.
一旦我们得到了迭代器对象,我们就可以使用hasNext()和next()方法进行迭代。
4.2. Finding the Shortest Path
4.2.寻找最短路径
It provides implementations of various algorithms such as Dijkstra, Bellman-Ford, Astar, and FloydWarshall in the org.jgrapht.alg.shortestpath package.
它在org.jgrapht.alg.shortestpath包中提供了各种算法的实现,如Dijkstra、Bellman-Ford、Astar和FloydWarshall。
Let’s find the shortest path using Dijkstra’s algorithm:
让我们用Dijkstra算法找到最短路径。
@Test
public void whenGetDijkstraShortestPath_thenGetNotNullPath() {
DijkstraShortestPath dijkstraShortestPath
= new DijkstraShortestPath(directedGraph);
List<String> shortestPath = dijkstraShortestPath
.getPath("v1","v4").getVertexList();
assertNotNull(shortestPath);
}Similarly, to get the shortest path using the Bellman-Ford algorithm:
同样地,要用Bellman-Ford算法得到最短路径。
@Test
public void
whenGetBellmanFordShortestPath_thenGetNotNullPath() {
BellmanFordShortestPath bellmanFordShortestPath
= new BellmanFordShortestPath(directedGraph);
List<String> shortestPath = bellmanFordShortestPath
.getPath("v1", "v4")
.getVertexList();
assertNotNull(shortestPath);
}4.3. Finding Strongly Connected Subgraphs
4.3.寻找强连接的子图
Before we get into the implementation, let’s briefly look at what strongly connected subgraphs mean. A subgraph is said to be strongly connected only if there is a path between each pair of its vertices.
在我们进入实施阶段之前,让我们简单地看看强连接子图的含义。只有当一个子图的每一对顶点之间都有一条路径时,才能说它是强连接的。
In our example, {v1,v2,v3,v4} can be considered a strongly connected subgraph if we can traverse to any vertex irrespective of what the current vertex is.
在我们的例子中,{v1,v2,v3,v4}可以被认为是一个强连接的子图,如果我们可以穿越到任何顶点,不管当前顶点是什么。
We can list four such subgraphs for the directed graph shown in the above image:
{v9},{v8},{v5,v6,v7},{v1,v2,v3,v4}
我们可以为上图中的有向图列出四个这样的子图:
{v9},{v8},{v5,v6,v7},{v1,v2,v3,v4}
Implementation to list out all strongly connected subgraphs:
实现列出所有强连接子图。
@Test
public void
whenGetStronglyConnectedSubgraphs_thenPathExists() {
StrongConnectivityAlgorithm<String, DefaultEdge> scAlg
= new KosarajuStrongConnectivityInspector<>(directedGraph);
List<DirectedSubgraph<String, DefaultEdge>> stronglyConnectedSubgraphs
= scAlg.stronglyConnectedSubgraphs();
List<String> stronglyConnectedVertices
= new ArrayList<>(stronglyConnectedSubgraphs.get(3)
.vertexSet());
String randomVertex1 = stronglyConnectedVertices.get(0);
String randomVertex2 = stronglyConnectedVertices.get(3);
AllDirectedPaths<String, DefaultEdge> allDirectedPaths
= new AllDirectedPaths<>(directedGraph);
List<GraphPath<String, DefaultEdge>> possiblePathList
= allDirectedPaths.getAllPaths(
randomVertex1, randomVertex2, false,
stronglyConnectedVertices.size());
assertTrue(possiblePathList.size() > 0);
}4.4. Eulerian Circuit
4.4.欧拉电路
A Eulerian Circuit in a graph G is a circuit that includes all vertices and edges of G. A graph which has it is a Eulerian Graph.
图G中的Eulerian电路是一个包括G所有顶点和边的电路。有这种回路的图就是欧拉图。
Let’s have a look at the graph:
让我们来看看这个图。
public void createGraphWithEulerianCircuit() {
SimpleWeightedGraph<String, DefaultEdge> simpleGraph
= new SimpleWeightedGraph<>(DefaultEdge.class);
IntStream.range(1,5)
.forEach(i-> simpleGraph.addVertex("v" + i));
IntStream.range(1,5)
.forEach(i-> {
int endVertexNo = (i + 1) > 5 ? 1 : i + 1;
simpleGraph.addEdge("v" + i,"v" + endVertexNo);
});
}Now, we can test whether a graph contains Eulerian Circuit using the API:
现在,我们可以使用API来测试一个图是否包含欧拉电路。
@Test
public void givenGraph_whenCheckEluerianCycle_thenGetResult() {
HierholzerEulerianCycle eulerianCycle
= new HierholzerEulerianCycle<>();
assertTrue(eulerianCycle.isEulerian(simpleGraph));
}
@Test
public void whenGetEulerianCycle_thenGetGraphPath() {
HierholzerEulerianCycle eulerianCycle
= new HierholzerEulerianCycle<>();
GraphPath path = eulerianCycle.getEulerianCycle(simpleGraph);
assertTrue(path.getEdgeList()
.containsAll(simpleGraph.edgeSet()));
}4.5. Hamiltonian Circuit
4.5.哈密尔顿电路
A GraphPath that visits each vertex exactly once is known as Hamiltonian Path.
一个精确访问每个顶点一次的GraphPath被称为Hamilton Path。
A Hamiltonian cycle (or Hamiltonian circuit) is a Hamiltonian Path such that there is an edge (in the graph) from the last vertex to the first vertex of the path.
哈密尔顿循环(或哈密尔顿回路)是一条哈密尔顿路径,使得(图中)有一条边从路径的最后一个顶点到第一个顶点。
We can find optimal Hamiltonian Cycle for complete graph with HamiltonianCycle.getApproximateOptimalForCompleteGraph() method.
我们可以用HamiltonianCycle.getApproximateOptimalForCompleteGraph()方法找到完整图形的最优哈密尔顿循环。
This method will return an approximate minimal traveling salesman tour (Hamiltonian cycle). The optimal solution is NP-complete, so this is a decent approximation that runs in polynomial time:
这个方法将返回一个近似的最小旅行推销员之旅(哈密尔顿循环)。最佳解是NP-完全的,所以这是一个体面的近似,在多项式时间内运行。
public void
whenGetHamiltonianCyclePath_thenGetVerticeSequence() {
List<String> verticeList = HamiltonianCycle
.getApproximateOptimalForCompleteGraph(completeGraph);
assertEquals(verticeList.size(), completeGraph.vertexSet().size());
}4.6. Cycle Detector
4.6.循环检测器
We can also check if there are any cycles in the graph. Currently, CycleDetector only supports directed graphs:
我们还可以检查图中是否存在任何周期。目前,CycleDetector只支持有向图。
@Test
public void whenCheckCycles_thenDetectCycles() {
CycleDetector<String, DefaultEdge> cycleDetector
= new CycleDetector<String, DefaultEdge>(directedGraph);
assertTrue(cycleDetector.detectCycles());
Set<String> cycleVertices = cycleDetector.findCycles();
assertTrue(cycleVertices.size() > 0);
}5. Graph Visualization
5.图形可视化
JGraphT allows us to generate visualizations of graphs and save them as images, first let’s add the jgrapht-ext extension dependency from Maven Central:
JGraphT允许我们生成图形的可视化,并将其保存为图片,首先让我们从Maven中心添加jgrapht-ext扩展依赖。
<dependency>
<groupId>org.jgrapht</groupId>
<artifactId>jgrapht-ext</artifactId>
<version>1.0.1</version>
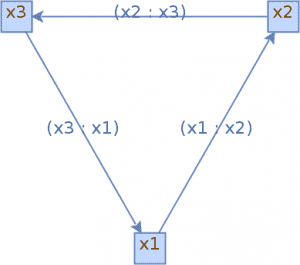
</dependency>Next, let’s create a simple directed graph with 3 vertices and 3 edges:
接下来,让我们创建一个有3个顶点和3条边的简单有向图。
@Before
public void createGraph() {
File imgFile = new File("src/test/resources/graph.png");
imgFile.createNewFile();
DefaultDirectedGraph<String, DefaultEdge> g =
new DefaultDirectedGraph<String, DefaultEdge>(DefaultEdge.class);
String x1 = "x1";
String x2 = "x2";
String x3 = "x3";
g.addVertex(x1);
g.addVertex(x2);
g.addVertex(x3);
g.addEdge(x1, x2);
g.addEdge(x2, x3);
g.addEdge(x3, x1);
}We can now visualize this graph:
我们现在可以把这个图形可视化。
@Test
public void givenAdaptedGraph_whenWriteBufferedImage_thenFileShouldExist() throws IOException {
JGraphXAdapter<String, DefaultEdge> graphAdapter =
new JGraphXAdapter<String, DefaultEdge>(g);
mxIGraphLayout layout = new mxCircleLayout(graphAdapter);
layout.execute(graphAdapter.getDefaultParent());
BufferedImage image =
mxCellRenderer.createBufferedImage(graphAdapter, null, 2, Color.WHITE, true, null);
File imgFile = new File("src/test/resources/graph.png");
ImageIO.write(image, "PNG", imgFile);
assertTrue(imgFile.exists());
}Here we have created a JGraphXAdapter which receives our graph as a constructor argument and we have applied a mxCircleLayout to it. This lays the visualization out in a circular manner.
在这里,我们创建了一个JGraphXAdapter,它接收了我们的图形作为构造参数,并且我们对它应用了一个mxCircleLayout。这将使可视化以一种圆形的方式呈现出来。
Furthermore, we use a mxCellRenderer to create a BufferedImage and then write the visualization to a png file.
此外,我们使用一个mxCellRenderer来创建一个BufferedImage,然后将可视化的内容写入一个png文件中。
We can see the final image in a browser or our favorite renderer:
我们可以在浏览器或我们最喜欢的渲染器中看到最终图像:。
We can find more details in the official documentation.
我们可以在官方文档中找到更多细节。
6. Conclusion
6.结论
JGraphT provides almost all types of graphs and variety of graph algorithms. We covered how to use few popular APIs. However, you can always explore the library on the official page.
JGraphT提供了几乎所有类型的图形和各种图形算法。我们介绍了如何使用少数流行的API。然而,你可以随时在官方页面上探索该库。
The implementation of all these examples and code snippets can be found over on Github.
所有这些例子和代码片断的实现都可以在Github上找到over。