1. Overview

1.概述

In this quick tutorial, we’ll show how to find the point of intersection of two lines defined by the linear functions in the slope-intercept form.

在这个快速教程中，我们将展示如何找到由线性函数定义的两条直线的交点，以斜面截距形式。

2. The Math Formula of Intersection

2.相交的数学公式

Any straight line (except vertical) on a plane can be defined by the linear function:

平面上的任何一条直线（垂直除外）都可以由线性函数来定义。

y = mx + b

where m is the slope and b is the y-intercept.

其中m是斜率，b是y截距。

For a vertical line, m would be equal to infinity, that’s why we’re excluding it. If two lines are parallel, they have the same slope, that is the same value of m.

对于垂直线来说，m将等于无穷大，这就是为什么我们要排除它。如果两条直线平行，它们的斜率相同，也就是m的值相同。

Let’s say we have two lines. The first function defines the first line:

假设我们有两行。第一个函数定义了第一行。

y = m1x + b1

And the second function defines the second line:

而第二个函数定义了第二行。

y = m2x + b2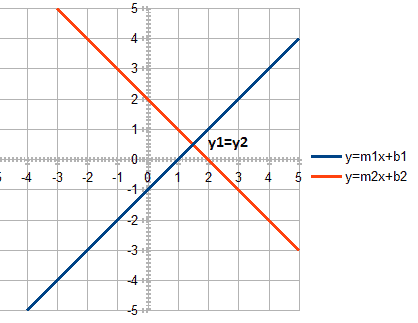

We want to find the point of intersection of these lines. Obviously, the equation is true for the point of intersection:

general-y1-y2
>
我们想找到这些线的交点。很明显，对于交点来说，方程是真实的。

y1 = y2

Let’s substitute y-variables:

让我们来替代y-变量。

m1x + b1 = m2x + b2

From the above equation we can find the x-coordinate:

从上述方程我们可以找到x-坐标：。

x(m1 - m2) = b2 - b1
x = (b2 - b1) / (m1 - m2)

Finally, we can find y-coordinate of the point of intersection:

最后，我们可以找到相交点的y坐标：。

y = m1x + b1

Let’s now move on to the implementation part.

现在让我们进入实施部分。

3. Java Implementation

3.Java实现

Firstly, we have four input variables – m1, b1 for the first line, and m2, b2 for the second line.

首先，我们有四个输入变量–m1, b1用于第一行，m2, b2用于第二行。

Secondly, we’ll convert the calculated point of intersection into the object of java.awt.Point type.

其次，我们将把计算出来的交点转换成java.awt.Point类型的对象。

Finally, lines may be parallel, hence let’s make the returned value Optional<Point>:

最后，线条可能是平行的，因此让我们把返回值变成Optional<Point>。

public Optional<Point> calculateIntersectionPoint(
    double m1, 
    double b1, 
    double m2, 
    double b2) {

    if (m1 == m2) {
        return Optional.empty();
    }

    double x = (b2 - b1) / (m1 - m2);
    double y = m1 * x + b1;

    Point point = new Point();
    point.setLocation(x, y);
    return Optional.of(point);
}

Now let’s choose some values and test the method for parallel and non-parallel lines.

现在让我们选择一些数值，测试一下平行线和非平行线的方法。

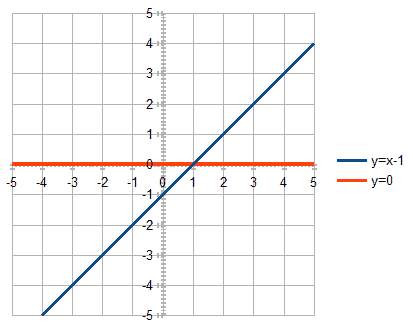
For example, let’s take the x-axis (y = 0) as the first line, and the line defined by y = x – 1 as the second line.

例如，让我们把x轴（y=0）作为第一条线，把由y=x-1定义的线作为第二条线。

For the second line, the slope m is equal to 1 which means 45 degrees, and the y-intercept is equal to -1 which means that the line intercepts the y-axis in the point (0, -1).

对于第二条直线，斜率m等于1，意味着45度，y截距等于-1，意味着直线在点（0，-1）上与y轴相交。

It’s intuitively clear that the point of intersection of the second line with the x-axis must be (1,0):

直观地讲，第二条线与x轴的交点必须是（1,0）。

Let’s check it.

让我们检查一下。

Firstly, let’s make sure that a Point is present, as the lines aren’t parallel, and then check the values of x and y:

首先，让我们确保有一个Point存在，因为这些线并不平行，然后检查x和y的值。

@Test
public void givenNotParallelLines_whenCalculatePoint_thenPresent() {
    double m1 = 0;
    double b1 = 0;
    double m2 = 1;
    double b2 = -1;

    Optional<Point> point = service.calculateIntersectionPoint(m1, b1, m2, b2);

    assertTrue(point.isPresent());
    assertEquals(point.get().getX(), 1, 0.001);
    assertEquals(point.get().getY(), 0, 0.001);
}

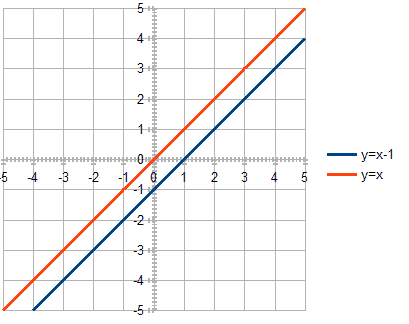
Lastly, let’s take two parallel lines and make sure that the returned value is empty:

最后，让我们采取两个平行线，并确保返回值为空。

@Test
public void givenParallelLines_whenCalculatePoint_thenEmpty() {
    double m1 = 1;
    double b1 = 0;
    double m2 = 1;
    double b2 = -1;

    Optional<Point> point = service.calculateIntersectionPoint(m1, b1, m2, b2);

    assertFalse(point.isPresent());
}

4. Conclusion

4.结论

In this tutorial, we’ve shown how to calculate the point of intersection of two lines.

在本教程中，我们已经展示了如何计算两条直线的交点。

As usual, the complete source code is available over on GitHub.

像往常一样，完整的源代码可以在GitHub上找到，。