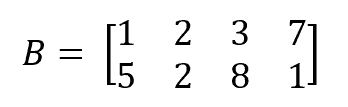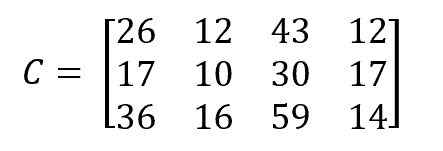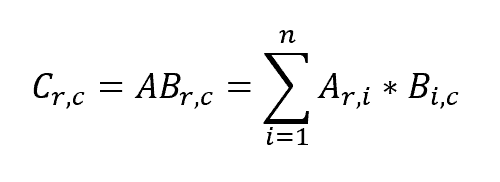1. Overview
1.概述
In this tutorial, we’ll have a look at how we can multiply two matrices in Java.
在本教程中,我们将看看如何在Java中实现两个矩阵的相乘。
As the matrix concept doesn’t exist natively in the language, we’ll implement it ourselves, and we’ll also work with a few libraries to see how they handle matrices multiplication.
由于矩阵的概念在语言中并不存在,我们将自己实现它,我们还将与一些库合作,看它们如何处理矩阵乘法。
In the end, we’ll do a little benchmarking of the different solutions we explored in order to determinate the fastest one.
最后,我们将对我们探索的不同解决方案做一个小小的基准测试,以确定最快的方案。
2. The Example
2.例子
Let’s begin by setting up an example we’ll be able to refer to throughout this tutorial.
让我们从设置一个例子开始,我们可以在本教程中参考。
First, we’ll imagine a 3×2 matrix:
首先,我们将想象一个3×2的矩阵。
Let’s now imagine a second matrix, two rows by four columns this time:
现在让我们想象一下第二个矩阵,这次是两行四列。
Then, the multiplication of the first matrix by the second matrix, which will result in a 3×4 matrix:
然后,第一个矩阵与第二个矩阵相乘,将得到一个3×4的矩阵。
As a reminder, this result is obtained by computing each cell of the resulting matrix with this formula:
作为提醒,这个结果是通过用这个公式计算所得矩阵的每个单元格而得到的。
Where r is the number of rows of matrix A, c is the number of columns of matrix B and n is the number of columns of matrix A, which must match the number of rows of matrix B.
其中,r是矩阵A的行数,c是矩阵B的列数,n是矩阵A的列数,必须与矩阵B的行数一致。
3. Matrix Multiplication
3.矩阵乘法
3.1. Own Implementation
3.1.自己的实施
Let’s start with our own implementation of matrices.
让我们从我们自己的矩阵的实现开始。
We’ll keep it simple and just use two dimensional double arrays:
我们将保持简单,只是使用二维的double arrays。
double[][] firstMatrix = {
new double[]{1d, 5d},
new double[]{2d, 3d},
new double[]{1d, 7d}
};
double[][] secondMatrix = {
new double[]{1d, 2d, 3d, 7d},
new double[]{5d, 2d, 8d, 1d}
};Those are the two matrices of our example. Let’s create the one expected as the result of their multiplication:
这就是我们例子中的两个矩阵。让我们创建一个预期的矩阵,作为它们相乘的结果。
double[][] expected = {
new double[]{26d, 12d, 43d, 12d},
new double[]{17d, 10d, 30d, 17d},
new double[]{36d, 16d, 59d, 14d}
};Now that everything is set up, let’s implement the multiplication algorithm. We’ll first create an empty result array and iterate through its cells to store the expected value in each one of them:
现在一切都设置好了,让我们来实现乘法算法。我们首先创建一个空的结果数组,然后遍历它的单元格,在每一个单元格中存储预期值:。
double[][] multiplyMatrices(double[][] firstMatrix, double[][] secondMatrix) {
double[][] result = new double[firstMatrix.length][secondMatrix[0].length];
for (int row = 0; row < result.length; row++) {
for (int col = 0; col < result[row].length; col++) {
result[row][col] = multiplyMatricesCell(firstMatrix, secondMatrix, row, col);
}
}
return result;
}Finally, let’s implement the computation of a single cell. In order to achieve that, we’ll use the formula shown earlier in the presentation of the example:
最后,让我们来实现单个单元格的计算。为了实现这一点,我们将使用前面介绍的公式。
double multiplyMatricesCell(double[][] firstMatrix, double[][] secondMatrix, int row, int col) {
double cell = 0;
for (int i = 0; i < secondMatrix.length; i++) {
cell += firstMatrix[row][i] * secondMatrix[i][col];
}
return cell;
}Finally, let’s check that the result of the algorithm matches our expected result:
最后,让我们检查一下该算法的结果是否与我们的预期结果相符。
double[][] actual = multiplyMatrices(firstMatrix, secondMatrix);
assertThat(actual).isEqualTo(expected);3.2. EJML
3.2 EJML
The first library we’ll look at is EJML, which stands for Efficient Java Matrix Library. At the time of writing this tutorial, it’s one of the most recently updated Java matrix libraries. Its purpose is to be as efficient as possible regarding calculation and memory usage.
我们要看的第一个库是EJML,它代表Efficient Java Matrix Library。在编写本教程时,它是最近更新的Java矩阵库之一。其目的是在计算和内存使用方面尽可能地高效。
We’ll have to add the dependency to the library in our pom.xml:
我们必须在我们的pom.xml中添加对该库的依赖性。
<dependency>
<groupId>org.ejml</groupId>
<artifactId>ejml-all</artifactId>
<version>0.38</version>
</dependency>We’ll use pretty much the same pattern as before: creating two matrices according to our example and check that the result of their multiplication is the one we calculated earlier.
我们将使用与之前基本相同的模式:根据我们的例子创建两个矩阵,并检查它们相乘的结果是否就是我们之前计算的结果。
So, let’s create our matrices using EJML. In order to achieve this, we’ll use the SimpleMatrix class offered by the library.
所以,让我们用EJML创建我们的矩阵。为了达到这个目的,我们将使用库中提供的SimpleMatrix类。
It can take a two dimension double array as input for its constructor:
它可以接受一个二维的double数组作为其构造函数的输入。
SimpleMatrix firstMatrix = new SimpleMatrix(
new double[][] {
new double[] {1d, 5d},
new double[] {2d, 3d},
new double[] {1d ,7d}
}
);
SimpleMatrix secondMatrix = new SimpleMatrix(
new double[][] {
new double[] {1d, 2d, 3d, 7d},
new double[] {5d, 2d, 8d, 1d}
}
);And now, let’s define our expected matrix for the multiplication:
现在,让我们定义一下我们的预期矩阵,用于乘法。
SimpleMatrix expected = new SimpleMatrix(
new double[][] {
new double[] {26d, 12d, 43d, 12d},
new double[] {17d, 10d, 30d, 17d},
new double[] {36d, 16d, 59d, 14d}
}
);Now that we’re all set up, let’s see how to multiply the two matrices together. The SimpleMatrix class offers a mult() method taking another SimpleMatrix as a parameter and returning the multiplication of the two matrices:
现在我们都准备好了,让我们看看如何将两个矩阵相乘。SimpleMatrix类提供了一个mult()方法,以另一个SimpleMatrix为参数,返回两个矩阵的乘法。
SimpleMatrix actual = firstMatrix.mult(secondMatrix);Let’s check if the obtained result matches the expected one.
让我们检查一下获得的结果是否与预期的一致。
As SimpleMatrix doesn’t override the equals() method, we can’t rely on it to do the verification. But, it offers an alternative: the isIdentical() method which takes not only another matrix parameter but also a double fault tolerance one to ignore small differences due to double precision:
由于SimpleMatrix没有覆盖equals()方法,我们不能依靠它来做验证。但是,它提供了一个替代方法:isIdentical()方法,它不仅需要另一个矩阵参数,还需要一个double容错参数,以忽略由于双精度造成的小差异。
assertThat(actual).matches(m -> m.isIdentical(expected, 0d));That concludes matrices multiplication with the EJML library. Let’s see what the other ones are offering.
EJML库的矩阵乘法就这样结束了。让我们看看其他的库都提供了什么。
3.3. ND4J
3.3.ND4J
Let’s now try the ND4J Library. ND4J is a computation library and is part of the deeplearning4j project. Among other things, ND4J offers matrix computation features.
现在让我们试试ND4J库。ND4J是一个计算库,是deeplearning4j项目的一部分。在其他方面,ND4J提供了矩阵计算功能。
First of all, we’ve to get the library dependency:
首先,我们要获得库的依赖性。
<dependency>
<groupId>org.nd4j</groupId>
<artifactId>nd4j-native</artifactId>
<version>1.0.0-beta4</version>
</dependency>Note that we’re using the beta version here because there seems to have some bugs with GA release.
请注意,我们在这里使用的是测试版,因为GA版似乎有一些错误。
For the sake of brevity, we won’t rewrite the two dimensions double arrays and just focus on how they are used with each library. Thus, with ND4J, we must create an INDArray. In order to do that, we’ll call the Nd4j.create() factory method and pass it a double array representing our matrix:
为了简洁起见,我们不会重写两个维度的double数组,而只是关注它们如何在每个库中使用。因此,对于ND4J,我们必须创建一个INDArray。为了做到这一点,我们将调用Nd4j.create()工厂方法,并传递给它一个代表我们的矩阵的double array。
INDArray matrix = Nd4j.create(/* a two dimensions double array */);As in the previous section, we’ll create three matrices: the two we’re going to multiply together and the one being the expected result.
和上一节一样,我们将创建三个矩阵:两个我们要相乘的矩阵和一个是预期结果。
After that, we want to actually do the multiplication between the first two matrices using the INDArray.mmul() method:
之后,我们要用INDArray.mmul()方法实际做前两个矩阵之间的乘法。
INDArray actual = firstMatrix.mmul(secondMatrix);Then, we check again that the actual result matches the expected one. This time we can rely on an equality check:
然后,我们再次检查实际结果是否与预期结果相符。这一次,我们可以依靠平等检查。
assertThat(actual).isEqualTo(expected);This demonstrates how the ND4J library can be used to do matrix calculations.
这展示了如何使用ND4J库来进行矩阵计算。
3.4. Apache Commons
3.4.Apache Commons
Let’s now talk about the Apache Commons Math3 module, which provides us with mathematic computations including matrices manipulations.
现在让我们来谈谈Apache Commons Math3模块,它为我们提供了数学计算,包括矩阵的操作。
Again, we’ll have to specify the dependency in our pom.xml:
同样,我们必须在我们的pom.xml中指定的依赖性。
<dependency>
<groupId>org.apache.commons</groupId>
<artifactId>commons-math3</artifactId>
<version>3.6.1</version>
</dependency>Once set up, we can use the RealMatrix interface and its Array2DRowRealMatrix implementation to create our usual matrices. The constructor of the implementation class takes a two-dimensional double array as its parameter:
一旦设置好,我们就可以使用RealMatrix接口及其Array2DRowRealMatrix实现来创建我们常用的矩阵。实现类的构造函数需要一个二维的double数组作为其参数。
RealMatrix matrix = new Array2DRowRealMatrix(/* a two dimensions double array */);As for matrices multiplication, the RealMatrix interface offers a multiply() method taking another RealMatrix parameter:
至于矩阵的乘法,RealMatrix接口提供了一个multiply()方法,接受另一个RealMatrix参数。
RealMatrix actual = firstMatrix.multiply(secondMatrix);We can finally verify that the result is equal to what we’re expecting:
我们最终可以验证结果是否等于我们所期望的。
assertThat(actual).isEqualTo(expected);Let’s see the next library!
让我们看看下一个图书馆!
3.5. LA4J
3.5.LA4J
This one’s named LA4J, which stands for Linear Algebra for Java.
这个名为LA4J,代表Java的线性代数。
Let’s add the dependency for this one as well:
让我们也为这个人添加依赖性。
<dependency>
<groupId>org.la4j</groupId>
<artifactId>la4j</artifactId>
<version>0.6.0</version>
</dependency>Now, LA4J works pretty much like the other libraries. It offers a Matrix interface with a Basic2DMatrix implementation that takes a two-dimensional double array as input:
现在,LA4J的工作方式与其他库差不多。它提供了一个Matrix接口,有一个Basic2DMatrix实现,它接受一个二维double数组作为输入。
Matrix matrix = new Basic2DMatrix(/* a two dimensions double array */);As in the Apache Commons Math3 module, the multiplication method is multiply() and takes another Matrix as its parameter:
和Apache Commons Math3模块一样,乘法方法是multiply(),并接受另一个Matrix作为其参数。
Matrix actual = firstMatrix.multiply(secondMatrix);Once again, we can check that the result matches our expectations:
再一次,我们可以检查结果是否符合我们的预期。
assertThat(actual).isEqualTo(expected);Let’s now have a look at our last library: Colt.
现在让我们来看看我们的最后一个图书馆。驹子。
3.6. Colt
3.6.驹子
Colt is a library developed by CERN. It provides features enabling high performance scientific and technical computing.
Colt是一个由CERN开发的库。它提供的功能使高性能的科学和技术计算成为可能。
As with the previous libraries, we must get the right dependency:
与之前的库一样,我们必须获得正确的依赖性。
<dependency>
<groupId>colt</groupId>
<artifactId>colt</artifactId>
<version>1.2.0</version>
</dependency>In order to create matrices with Colt, we must make use of the DoubleFactory2D class. It comes with three factory instances: dense, sparse and rowCompressed. Each is optimized to create the matching kind of matrix.
为了用Colt创建矩阵,我们必须利用DoubleFactory2D类。它有三个工厂实例。密集、稀疏和行压缩。每个实例都被优化以创建匹配的矩阵类型。
For our purpose, we’ll use the dense instance. This time, the method to call is make() and it takes a two-dimensional double array again, producing a DoubleMatrix2D object:
为了我们的目的,我们将使用dense实例。这一次,要调用的方法是make(),它再次接收一个二维的double array,产生一个DoubleMatrix2D对象。
DoubleMatrix2D matrix = doubleFactory2D.make(/* a two dimensions double array */);Once our matrices are instantiated, we’ll want to multiply them. This time, there’s no method on the matrix object to do that. We’ve got to create an instance of the Algebra class which has a mult() method taking two matrices for parameters:
一旦我们的矩阵被实例化了,我们就想把它们相乘。这一次,矩阵对象上没有任何方法可以做到这一点。我们必须创建一个Algebra类的实例,该类有一个mult()方法,以两个矩阵作为参数。
Algebra algebra = new Algebra();
DoubleMatrix2D actual = algebra.mult(firstMatrix, secondMatrix);Then, we can compare the actual result to the expected one:
然后,我们可以将实际结果与预期结果进行比较。
assertThat(actual).isEqualTo(expected);4. Benchmarking
4.基准测试
Now that we’re done with exploring the different possibilities of matrix multiplication, let’s check which are the most performant.
现在我们已经完成了对矩阵乘法的不同可能性的探索,让我们来检查一下哪些是最有性能的。
4.1. Small Matrices
4.1.小矩阵
Let’s begin with small matrices. Here, a 3×2 and a 2×4 matrices.
让我们从小矩阵开始。这里有一个3×2和一个2×4的矩阵。
In order to implement the performance test, we’ll use the JMH benchmarking library. Let’s configure a benchmarking class with the following options:
为了实现性能测试,我们将使用JMH基准测试库。让我们用以下选项来配置一个基准测试类。
public static void main(String[] args) throws Exception {
Options opt = new OptionsBuilder()
.include(MatrixMultiplicationBenchmarking.class.getSimpleName())
.mode(Mode.AverageTime)
.forks(2)
.warmupIterations(5)
.measurementIterations(10)
.timeUnit(TimeUnit.MICROSECONDS)
.build();
new Runner(opt).run();
}This way, JMH will make two full runs for each method annotated with @Benchmark, each with five warmup iterations (not taken into the average computation) and ten measurement ones. As for the measurements, it’ll gather the average time of execution of the different libraries, in microseconds.
这样,JMH将为每个注有@Benchmark的方法进行两次完整的运行,每次有五个热身迭代(不计入平均计算)和十个测量迭代。至于测量,它将收集不同库的平均执行时间,以微秒为单位。
We then have to create a state object containing our arrays:
然后我们必须创建一个包含我们的数组的状态对象。
@State(Scope.Benchmark)
public class MatrixProvider {
private double[][] firstMatrix;
private double[][] secondMatrix;
public MatrixProvider() {
firstMatrix =
new double[][] {
new double[] {1d, 5d},
new double[] {2d, 3d},
new double[] {1d ,7d}
};
secondMatrix =
new double[][] {
new double[] {1d, 2d, 3d, 7d},
new double[] {5d, 2d, 8d, 1d}
};
}
}That way, we make sure arrays initialization is not part of the benchmarking. After that, we still have to create methods that do the matrices multiplication, using the MatrixProvider object as the data source. We won’t repeat the code here as we saw each library earlier.
这样,我们就能确保数组的初始化不是基准测试的一部分。在这之后,我们仍然要创建做矩阵乘法的方法,使用MatrixProvider对象作为数据源。我们不会在这里重复代码,因为我们在前面看到了每个库。
Finally, we’ll run the benchmarking process using our main method. This gives us the following result:
最后,我们将使用我们的main方法运行基准测试过程。这给了我们以下的结果。
Benchmark Mode Cnt Score Error Units
MatrixMultiplicationBenchmarking.apacheCommonsMatrixMultiplication avgt 20 1,008 ± 0,032 us/op
MatrixMultiplicationBenchmarking.coltMatrixMultiplication avgt 20 0,219 ± 0,014 us/op
MatrixMultiplicationBenchmarking.ejmlMatrixMultiplication avgt 20 0,226 ± 0,013 us/op
MatrixMultiplicationBenchmarking.homemadeMatrixMultiplication avgt 20 0,389 ± 0,045 us/op
MatrixMultiplicationBenchmarking.la4jMatrixMultiplication avgt 20 0,427 ± 0,016 us/op
MatrixMultiplicationBenchmarking.nd4jMatrixMultiplication avgt 20 12,670 ± 2,582 us/opAs we can see, EJML and Colt are performing really well with about a fifth of a microsecond per operation, where ND4j is less performant with a bit more than ten microseconds per operation. The other libraries have performances situated in between.
我们可以看到,EJML和Colt的性能非常好,每次操作只需五分之一微秒,而ND4j的性能较差,每次操作要超过十微秒。其他库的性能介于两者之间。
Also, it’s worth noting that when increasing the number of warmup iterations from 5 to 10, performance is increasing for all the libraries.
另外,值得注意的是,当热身迭代次数从5次增加到10次时,所有库的性能都在增加。
4.2. Large Matrices
4.2.大型矩阵
Now, what happens if we take larger matrices, like 3000×3000? To check what happens, let’s first create another state class providing generated matrices of that size:
现在,如果我们采取更大的矩阵,如3000×3000,会发生什么?为了检查会发生什么,让我们首先创建另一个状态类,提供生成该尺寸的矩阵。
@State(Scope.Benchmark)
public class BigMatrixProvider {
private double[][] firstMatrix;
private double[][] secondMatrix;
public BigMatrixProvider() {}
@Setup
public void setup(BenchmarkParams parameters) {
firstMatrix = createMatrix();
secondMatrix = createMatrix();
}
private double[][] createMatrix() {
Random random = new Random();
double[][] result = new double[3000][3000];
for (int row = 0; row < result.length; row++) {
for (int col = 0; col < result[row].length; col++) {
result[row][col] = random.nextDouble();
}
}
return result;
}
}As we can see, we’ll create 3000×3000 two-dimensions double arrays filled with random real numbers.
正如我们所看到的,我们将创建3000×3000个充满随机实数的二维数组。
Let’s now create the benchmarking class:
现在让我们来创建基准测试类。
public class BigMatrixMultiplicationBenchmarking {
public static void main(String[] args) throws Exception {
Map<String, String> parameters = parseParameters(args);
ChainedOptionsBuilder builder = new OptionsBuilder()
.include(BigMatrixMultiplicationBenchmarking.class.getSimpleName())
.mode(Mode.AverageTime)
.forks(2)
.warmupIterations(10)
.measurementIterations(10)
.timeUnit(TimeUnit.SECONDS);
new Runner(builder.build()).run();
}
@Benchmark
public Object homemadeMatrixMultiplication(BigMatrixProvider matrixProvider) {
return HomemadeMatrix
.multiplyMatrices(matrixProvider.getFirstMatrix(), matrixProvider.getSecondMatrix());
}
@Benchmark
public Object ejmlMatrixMultiplication(BigMatrixProvider matrixProvider) {
SimpleMatrix firstMatrix = new SimpleMatrix(matrixProvider.getFirstMatrix());
SimpleMatrix secondMatrix = new SimpleMatrix(matrixProvider.getSecondMatrix());
return firstMatrix.mult(secondMatrix);
}
@Benchmark
public Object apacheCommonsMatrixMultiplication(BigMatrixProvider matrixProvider) {
RealMatrix firstMatrix = new Array2DRowRealMatrix(matrixProvider.getFirstMatrix());
RealMatrix secondMatrix = new Array2DRowRealMatrix(matrixProvider.getSecondMatrix());
return firstMatrix.multiply(secondMatrix);
}
@Benchmark
public Object la4jMatrixMultiplication(BigMatrixProvider matrixProvider) {
Matrix firstMatrix = new Basic2DMatrix(matrixProvider.getFirstMatrix());
Matrix secondMatrix = new Basic2DMatrix(matrixProvider.getSecondMatrix());
return firstMatrix.multiply(secondMatrix);
}
@Benchmark
public Object nd4jMatrixMultiplication(BigMatrixProvider matrixProvider) {
INDArray firstMatrix = Nd4j.create(matrixProvider.getFirstMatrix());
INDArray secondMatrix = Nd4j.create(matrixProvider.getSecondMatrix());
return firstMatrix.mmul(secondMatrix);
}
@Benchmark
public Object coltMatrixMultiplication(BigMatrixProvider matrixProvider) {
DoubleFactory2D doubleFactory2D = DoubleFactory2D.dense;
DoubleMatrix2D firstMatrix = doubleFactory2D.make(matrixProvider.getFirstMatrix());
DoubleMatrix2D secondMatrix = doubleFactory2D.make(matrixProvider.getSecondMatrix());
Algebra algebra = new Algebra();
return algebra.mult(firstMatrix, secondMatrix);
}
}When we run this benchmarking, we obtain completely different results:
当我们运行这个基准测试时,我们得到了完全不同的结果。
Benchmark Mode Cnt Score Error Units
BigMatrixMultiplicationBenchmarking.apacheCommonsMatrixMultiplication avgt 20 511.140 ± 13.535 s/op
BigMatrixMultiplicationBenchmarking.coltMatrixMultiplication avgt 20 197.914 ± 2.453 s/op
BigMatrixMultiplicationBenchmarking.ejmlMatrixMultiplication avgt 20 25.830 ± 0.059 s/op
BigMatrixMultiplicationBenchmarking.homemadeMatrixMultiplication avgt 20 497.493 ± 2.121 s/op
BigMatrixMultiplicationBenchmarking.la4jMatrixMultiplication avgt 20 35.523 ± 0.102 s/op
BigMatrixMultiplicationBenchmarking.nd4jMatrixMultiplication avgt 20 0.548 ± 0.006 s/opAs we can see, the homemade implementations and the Apache library are now way worse than before, taking nearly 10 minutes to perform the multiplication of the two matrices.
我们可以看到,现在自制的实现和Apache库比以前差多了,要花将近10分钟才能完成两个矩阵的乘法。
Colt is taking a bit more than 3 minutes, which is better but still very long. EJML and LA4J are performing pretty well as they run in nearly 30 seconds. But, it’s ND4J which wins this benchmarking performing in under a second on a CPU backend.
驹子的时间比3分钟多一点,这要好一些,但仍然很漫长。EJML和LA4J的表现相当好,它们的运行时间接近30秒。但是,ND4J在CPU后端上以不到一秒的时间表现赢得了这项基准测试。
4.3. Analysis
4.3.分析报告
That shows us that the benchmarking results really depend on the matrices’ characteristics and therefore it’s tricky to point out a single winner.
这向我们表明,基准测试结果确实取决于矩阵的特性,因此要指出一个单一的赢家是很棘手的。
5. Conclusion
5.总结
In this article, we’ve learned how to multiply matrices in Java, either by ourselves or with external libraries. After exploring all solutions, we did a benchmark of all of them and saw that, except for ND4J, they all performed pretty well on small matrices. On the other hand, on larger matrices, ND4J is taking the lead.
在这篇文章中,我们已经学会了如何在Java中进行矩阵乘法,可以自己操作,也可以使用外部库。在探索了所有的解决方案之后,我们对所有的解决方案做了一个基准测试,看到除了ND4J之外,它们在小矩阵上的表现都相当好。另一方面,在较大的矩阵上,ND4J则处于领先地位。
As usual, the full code for this article can be found over on GitHub.
像往常一样,本文的完整代码可以在GitHub上找到超过。