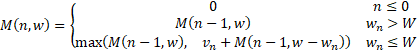1. Introduction

1.绪论

The knapsack problem is a combinatorial optimization problem that has many applications. In this tutorial, we’ll solve this problem in Java.

结包问题是一个组合优化问题，有很多应用。在本教程中，我们将用Java解决这个问题。

2. The Knapsack Problem

2.结包问题

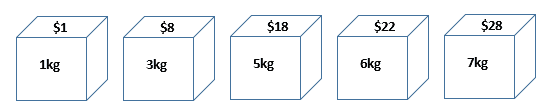
In the knapsack problem, we have a set of items. Each item has a weight and a worth value:

在knapsack问题中，我们有一组物品。每个项目都有一个权重和一个价值。

We want to put these items into a knapsack. However, it has a weight limit:

我们想把这些物品放进一个背包里。然而，它有一个重量限制。

Therefore, we need to choose the items whose total weight does not exceed the weight limit, and their total value is as high as possible. For example, the best solution for the above example is to choose the 5kg item and 6kg item, which gives a maximum value of $40 within the weight limit.

因此，我们需要选择总重量不超过重量限制的物品，并且其总价值越高越好。例如，上述例子的最佳方案是选择5公斤的物品和6公斤的物品，这样在重量限制范围内的最高价值为40美元。

The knapsack problem has several variations. In this tutorial, we will focus on the 0-1 knapsack problem. In the 0-1 knapsack problem, each item must either be chosen or left behind. We cannot take a partial amount of an item. Also, we cannot take an item multiple times.

结包问题有几种变化。在本教程中，我们将重点讨论0-1 knapsack问题。在0-1结包问题中，每个项目都必须被选择或留下。此外，我们也不能多次取走一个物品。

3. Mathematical Definition

3.数学定义

Let’s now formalize the 0-1 knapsack problem in mathematical notation. Given a set of n items and the weight limit W, we can define the optimization problem as:

现在让我们用数学符号来正式说明0-1背包问题。给定一组n物品和重量限制W，我们可以将优化问题定义为：。

This problem is NP-hard. Therefore, there is no polynomial-time algorithm to solve it currently. However, there is a pseudo-polynomial time algorithm using dynamic programming for this problem.

这个问题是NP-hard。因此，目前还没有解决它的多项式时间算法。然而，有一个伪多项式时间算法使用动态编程来解决这个问题。

4. Recursive Solution

4.递归解决方案

We can use a recursion formula to solve this problem:

我们可以用一个递归公式来解决这个问题。

In this formula, M(n,w) is the optimal solution for n items with a weight limit w. It is the maximum of the following two values:

在这个公式中，M(n,w)是n物品的最佳解决方案，重量限制w。它是以下两个值的最大值。

The optimal solution from (n-1) items with the weight limit w (excluding the n-th item)
Value of the n-th item plus the optimal solution from (n-1) items and w minus weight of the n-th item (including the n-th item)

If the weight of the n-th item is more than the current weight limit, we don’t include it. Therefore, it is in the first category of the above two cases.

如果n-th物品的重量超过当前的重量限制，我们不包括它。因此，它属于上述两种情况中的第一类。

We can implement this recursion formula in Java:

我们可以用Java实现这个递归公式。

int knapsackRec(int[] w, int[] v, int n, int W) {
    if (n <= 0) { 
        return 0; 
    } else if (w[n - 1] > W) {
        return knapsackRec(w, v, n - 1, W);
    } else {
        return Math.max(knapsackRec(w, v, n - 1, W), v[n - 1] 
          + knapsackRec(w, v, n - 1, W - w[n - 1]));
    }
}

In each recursion step, we need to evaluate two sub-optimal solutions. Therefore, the running time of this recursive solution is O(2ⁿ).

在每个递归步骤中，我们需要评估两个次优解。因此，这个递归解决方案的运行时间为O(2ⁿ)。

5. Dynamic Programming Solution

5.动态编程解决方案

Dynamic programming is a strategy for linearizing otherwise exponentially-difficult programming problems. The idea is to store the results of subproblems so that we do not have to re-compute them later.

动态编程是一种将其他指数级困难的编程问题线性化的策略。其理念是存储子问题的结果，这样我们就不必在以后重新计算。

We can also solve the 0-1 knapsack problem with dynamic programming. To use dynamic programming, we first create a 2-dimensional table with dimensions from 0 to n and 0 to W. Then, we use a bottom-up approach to calculate the optimal solution with this table:

我们也可以用动态编程来解决0-1 knapsack问题。为了使用动态编程，我们首先创建一个二维表，尺寸从0到n和0到W。然后，我们用一个自下而上的方法来计算这个表的最优解。

int knapsackDP(int[] w, int[] v, int n, int W) {
    if (n <= 0 || W <= 0) {
        return 0;
    }

    int[][] m = new int[n + 1][W + 1];
    for (int j = 0; j <= W; j++) {
        m[0][j] = 0;
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= W; j++) { 
            if (w[i - 1] > j) {
                m[i][j] = m[i - 1][j];
            } else {
                m[i][j] = Math.max(
                  m[i - 1][j], 
                  m[i - 1][j - w[i - 1]] + v[i - 1]);
            }
        }
    }
    return m[n][W];
}

In this solution, we have a nested loop over the item number n and the weight limit W. Therefore, it’s running time is O(nW).

在这个解决方案中，我们对物品数量n和重量限制W有一个嵌套循环。因此，它的运行时间是O（nW）。

6. Conclusion

6.结语

In this tutorial, we showed a math definition of the 0-1 knapsack problem. Then we provided a recursive solution to this problem with Java implementation. Finally, we used dynamic programming to solve this problem.

在本教程中，我们展示了0-1结包问题的数学定义。然后，我们为这个问题提供了一个用Java实现的递归解决方案。最后，我们用动态编程来解决这个问题。

As always, the source code for the article is available over on GitHub.

一如既往，该文章的源代码可在GitHub上获取。