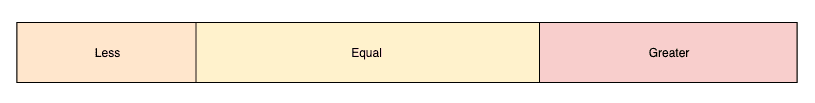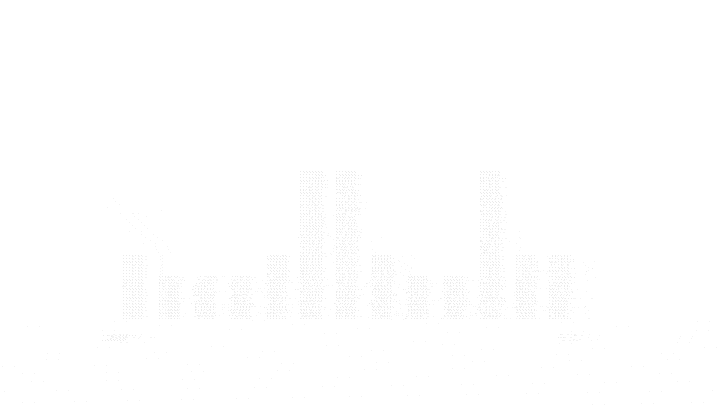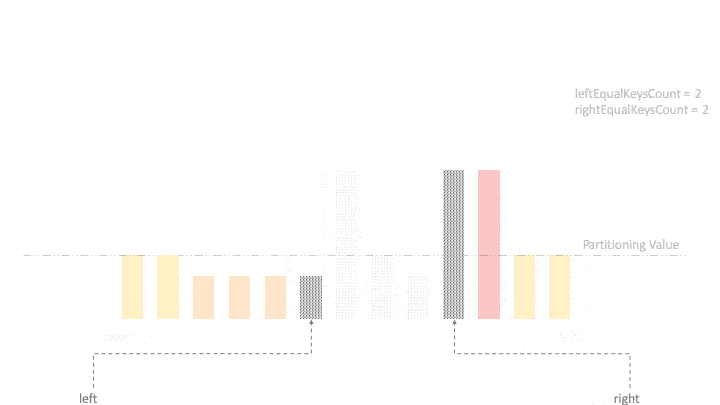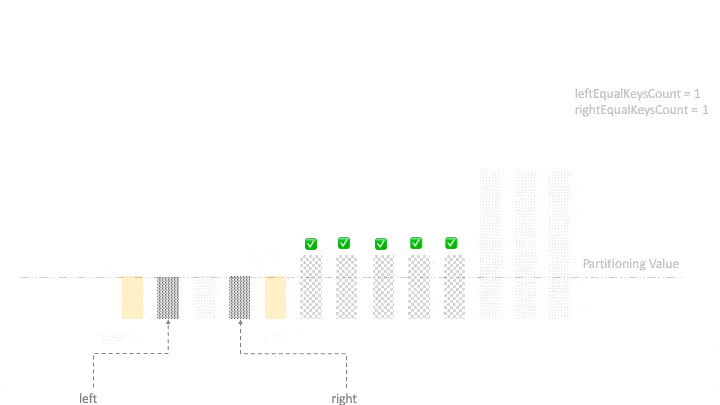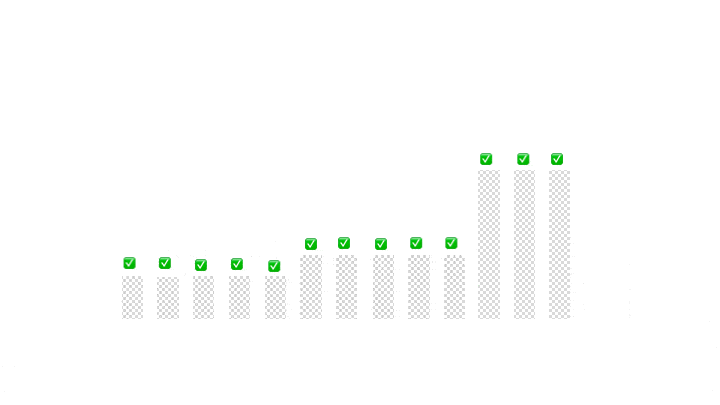Partitioning and Sorting Arrays with Many Repeated Entries with Java Examples – 用Java实例对有许多重复条目的数组进行分区和排序

1. Overview

1.概述

The run-time complexity of algorithms is often dependent on the nature of the input.

算法的运行时间复杂性往往取决于输入的性质。

In this tutorial, we’ll see how the trivial implementation of the Quicksort algorithm has a poor performance for repeated elements.

在本教程中，我们将看到Quicksort算法的简单实现对于重复元素的性能是如何的差。

Further, we’ll learn a few Quicksort variants to efficiently partition and sort inputs with a high density of duplicate keys.

此外，我们将学习一些Quicksort的变体，以有效地划分和排序具有高密度重复键的输入。

2. Trivial Quicksort

2.琐碎的quicksort

Quicksort is an efficient sorting algorithm based on the divide and conquer paradigm. Functionally speaking, it operates in-place on the input array and rearranges the elements with simple comparison and swap operations.

Quicksort是一种基于分而治之范式的高效排序算法。从功能上讲，它对输入数组进行就地操作，并通过简单的比较和交换操作重新排列元素。

2.1. Single-pivot Partitioning

2.1.单支点分区

A trivial implementation of the Quicksort algorithm relies heavily on a single-pivot partitioning procedure. In other words, partitioning divides the array A=[a_p, a_p+1, a_p+2,…, a_r] into two parts A[p..q] and A[q+1..r] such that:

Quicksort算法的一个微不足道的实现在很大程度上依赖于一个单支点的分区程序。换句话说，分区将数组A=[a_p, a_p+1, a_p+2,…, a_r]分为两部分A[p…q]和A[q+1…r]，这样。

• All elements in the first partition, A[p..q] are lesser than or equal to the pivot value A[q]
• All elements in the second partition, A[q+1..r] are greater than or equal to the pivot value A[q]

After that, the two partitions are treated as independent input arrays and fed themselves to the Quicksort algorithm. Let’s see Lomuto’s Quicksort in action:

之后，这两个分区被视为独立的输入数组，并将它们自己送入Quicksort算法。让我们看看Lomuto的Quicksort的运行情况。

2.2. Performance with Repeated Elements

2.2.重复元素的性能

Let’s say we have an array A = [4, 4, 4, 4, 4, 4, 4] that has all equal elements.

假设我们有一个数组A=[4，4，4，4，4，4]，它的元素都是相等的。

On partitioning this array with the single-pivot partitioning scheme, we’ll get two partitions. The first partition will be empty, while the second partition will have N-1 elements. Further, each subsequent invocation of the partition procedure will reduce the input size by only one. Let’s see how it works:

在用单支点分区方案对这个数组进行分区时，我们会得到两个分区。第一个分区将是空的，而第二个分区将有N-1个元素。此外，每个后续的分区程序的调用将使输入的大小只减少一个。让我们看看它是如何工作的。

Since the partition procedure has linear time complexity, the overall time complexity, in this case, is quadratic. This is the worst-case scenario for our input array.

由于分区程序具有线性时间复杂度，在这种情况下，整体时间复杂度是二次的。这是我们的输入阵列的最坏情况。

3. Three-way Partitioning

3.三向分区

To efficiently sort an array having a high number of repeated keys, we can choose to handle the equal keys more responsibly. The idea is to place them in the right position when we first encounter them. So, what we’re looking for is a three partition state of the array:

为了有效地对一个有大量重复键的数组进行排序，我们可以选择更负责任地处理相等键。我们的想法是，当我们第一次遇到它们时，把它们放在正确的位置上。所以，我们要找的是数组的三个分区状态。

• The left-most partition contains elements which are strictly less than the partitioning key
• The middle partition contains all elements which are equal to the partitioning key
• The right-most partition contains all elements which are strictly greater than the partitioning key

We’ll now dive deeper into a couple of approaches that we can use to achieve three-way partitioning.

现在我们将深入探讨我们可以用来实现三向分区的几种方法。

4. Dijkstra’s Approach

4.Dijkstra的方法

Dijkstra’s approach is an effective way of doing three-way partitioning. To understand this, let’s look into a classic programming problem.

Dijkstra的方法是一种有效的三向划分的方法。为了理解这一点，我们来看看一个经典的编程问题。

4.1. Dutch National Flag Problem

4.1.荷兰国旗问题

Inspired by the tricolor flag of the Netherlands, Edsger Dijkstra proposed a programming problem called the Dutch National Flag Problem (DNF).

受荷兰三色国旗的启发，Edsger Dijkstra提出了一个称为荷兰国旗问题（DNF）的编程问题。

In a nutshell, it’s a rearrangement problem where we’re given balls of three colors placed randomly in a line, and we’re asked to group the same colored balls together. Moreover, the rearrangement must ensure that groups follow the correct order.

简而言之，这是一个重新排列的问题，我们得到了随机放在一条线上的三种颜色的球，我们被要求将相同颜色的球组合在一起。此外，重新排列必须确保分组遵循正确的顺序。

Interestingly, the DNF problem makes a striking analogy with the 3-way partitioning of an array with repeated elements.

有趣的是，DNF问题与具有重复元素的数组的3-way分区有着惊人的相似性。

We can categorize all the numbers of an array into three groups with respect to a given key:

我们可以将一个数组的所有数字按照给定的键分为三组。

• The Red group contains all elements that are strictly lesser than the key
• The White group contains all elements that are equal to the key
• The Blue group contains all elements that strictly greater than the key

4.2. Algorithm

4.2.算法

One of the approaches to solve the DNF problem is to pick the first element as the partitioning key and scan the array from left to right. As we check each element, we move it to its correct group, namely Lesser, Equal, and Greater.

解决DNF问题的方法之一是挑选第一个元素作为分区键，从左到右扫描数组。当我们检查每个元素时，我们把它移到正确的组中，即小、等、大。

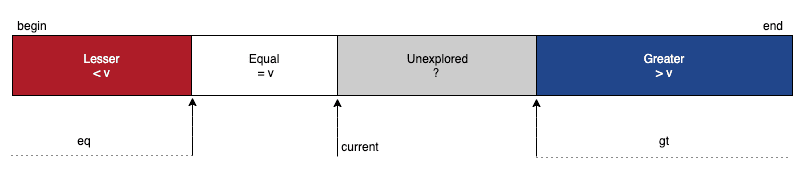
To keep track of our partitioning progress, we’d need the help of three pointers, namely lt, current, and gt. At any point in time, the elements to the left of lt will be strictly less than the partitioning key, and the elements to the right of gt will be strictly greater than the key.

为了跟踪我们的分区进度，我们需要三个指针的帮助，即lt、current和gt。在任何时间点，lt左边的元素将严格小于分区键，而gt右边的元素将严格大于键。

Further, we’ll use the current pointer for scanning, which means that all elements lying between the current and gt pointers are yet to be explored:

此外，我们将使用current指针进行扫描，这意味着位于current和gt指针之间的所有元素都有待探索。

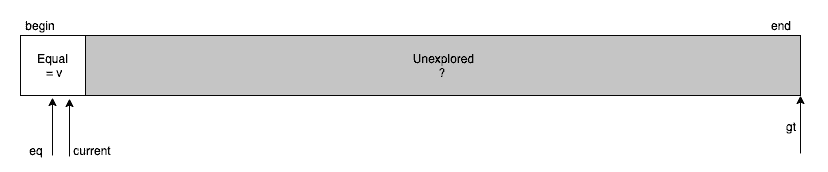
To begin with, we can set lt and current pointers at the very beginning of the array and the gt pointer at the very end of it:

首先，我们可以在数组的最开始设置lt和current指针，在数组的最末端设置gt指针。

For each element read via the current pointer, we compare it with the partitioning key and take one of the three composite actions:

对于每个通过current指针读取的元素，我们将其与分区键进行比较，并采取三种复合行动之一。

• If input[current] < key, then we exchange input[current] and input[lt] and increment both current and lt pointers
• If input[current] == key, then we increment current pointer
• If input[current] > key, then we exchange input[current] and input[gt] and decrement gt

Eventually, we’ll stop when the current and gt pointers cross each other. With that, the size of the unexplored region reduces to zero, and we’ll be left with only three required partitions.

最终，当current和gt指针相互交叉时，我们会停止。这样一来，未开发区域的大小就减少到了零，我们将只剩下三个需要的分区。

Finally, let’s see how this algorithm works on an input array having duplicate elements:

最后，让我们看看这个算法在一个有重复元素的输入数组上是如何工作的。

4.3. Implementation

4.3.实施

First, let’s write a utility procedure named compare() to do a three-way comparison between two numbers:

首先，让我们编写一个名为compare()的实用程序，在两个数字之间做一个三向比较。

public static int compare(int num1, int num2) {
    if (num1 > num2)
        return 1;
    else if (num1 < num2)
        return -1;
    else
        return 0;
}

Next, let’s add a method called swap() to exchange elements at two indices of the same array:

接下来，让我们添加一个名为swap()的方法来交换同一数组中两个索引上的元素。

public static void swap(int[] array, int position1, int position2) {
    if (position1 != position2) {
        int temp = array[position1];
        array[position1] = array[position2];
        array[position2] = temp;
    }
}

To uniquely identify a partition in the array, we’ll need its left and right boundary-indices. So, let’s go ahead and create a Partition class:

为了唯一地识别数组中的一个分区，我们需要它的左右边界索引。所以，让我们继续创建一个Partition类。

public class Partition {
    private int left;
    private int right;
}

Now, we’re ready to write our three-way partition() procedure:

现在，我们准备编写我们的三方partition()过程。

public static Partition partition(int[] input, int begin, int end) {
    int lt = begin, current = begin, gt = end;
    int partitioningValue = input[begin];

    while (current <= gt) {
        int compareCurrent = compare(input[current], partitioningValue);
        switch (compareCurrent) {
            case -1:
                swap(input, current++, lt++);
                break;
            case 0:
                current++;
                break;
            case 1:
                swap(input, current, gt--);
                break;
        }
    }
    return new Partition(lt, gt);
}

Finally, let’s write a quicksort() method that leverages our 3-way partitioning scheme to sort the left and right partitions recursively:

最后，让我们写一个quicksort()方法，利用我们的3-way分区方案对左右分区进行递归排序。

public static void quicksort(int[] input, int begin, int end) {
    if (end <= begin)
        return;

    Partition middlePartition = partition(input, begin, end);

    quicksort(input, begin, middlePartition.getLeft() - 1);
    quicksort(input, middlePartition.getRight() + 1, end);
}

5. Bentley-McIlroy’s Approach

5.本特利-麦克罗伊的方法

Jon Bentley and Douglas McIlroy co-authored an optimized version of the Quicksort algorithm. Let’s understand and implement this variant in Java:

Jon Bentley和Douglas McIlroy合著了一个Quicksort算法的优化版本。让我们来了解并在Java中实现这个变体。

5.1. Partitioning Scheme

5.1.分区方案

The crux of the algorithm is an iteration-based partitioning scheme. In the start, the entire array of numbers is an unexplored territory for us:

该算法的核心是一个基于迭代的分区方案。在开始时，整个数组对我们来说是一个未开发的领域。

We then start exploring the elements of the array from the left and right direction. Whenever we enter or leave the loop of exploration, we can visualize the array as a composition of five regions:

然后我们开始从左右两个方向探索数组中的元素。每当我们进入或离开探索的循环时，我们可以将数组可视化为五个区域的组成。

• On the extreme two ends, lies the regions having elements that are equal to the partitioning value
• The unexplored region stays in the center and its size keeps on shrinking with each iteration
• On the left of the unexplored region lies all elements lesser than the partitioning value
• On the right side of the unexplored region are elements greater than the partitioning value

Eventually, our loop of exploration terminates when there are no elements to be explored anymore. At this stage, the size of the unexplored region is effectively zero, and we’re left with only four regions:

最终，我们的探索循环在不再有任何元素可供探索时终止。在这个阶段，未探索区域的大小实际上是零，而我们只剩下四个区域。

Next, we move all the elements from the two equal-regions in the center so that there is only one equal-region in the center surrounding by the less-region on the left and the greater-region on the right. To do so, first, we swap the elements in the left equal-region with the elements on the right end of the less-region. Similarly, the elements in the right equal-region are swapped with the elements on the left end of the greater-region.

接下来，我们将所有的元素从中间的两个等区中移出，这样中间就只有一个等区，由左边的小区和右边的大区围绕。要做到这一点，首先，我们将左边等区的元素与少区右端的元素进行交换。同样地，右等区的元素与大区的左端元素互换。

Finally, we’ll be left with only three partitions, and we can further use the same approach to partition the less and the greater regions.

最后，我们将只剩下三个分区，我们可以进一步用同样的方法来划分小区域和大区域。

5.2. Implementation

5.2.实施

In our recursive implementation of the three-way Quicksort, we’ll need to invoke our partition procedure for sub-arrays that’ll have a different set of lower and upper bounds. So, our partition() method must accept three inputs, namely the array along with its left and right bounds.

在我们的三向Quicksort的递归实现中，我们需要为子数组调用我们的partition程序，这些子数组将有一组不同的下限和上限。因此，我们的partition()方法必须接受三个输入，即数组和它的左、右边界。

public static Partition partition(int input[], int begin, int end){
	// returns partition window
}

For simplicity, we can choose the partitioning value as the last element of the array. Also, let’s define two variables left=begin and right=end to explore the array inward.

为了简单起见，我们可以选择分区值作为数组的最后一个元素。另外，让我们定义两个变量left=begin和right=end来向内探索阵列。

Further, We’ll also need to keep track of the number of equal elements lying on the leftmost and rightmost. So, let’s initialize leftEqualKeysCount=0 and rightEqualKeysCount=0, and we’re now ready to explore and partition the array.

此外，我们还需要跟踪位于最左边和最右边的相等元素的数量。所以，让我们初始化leftEqualKeysCount=0和rightEqualKeysCount=0，我们现在准备探索和分割数组。

First, we start moving from both the directions and find an inversion where an element on the left is not less than partitioning value, and an element on the right is not greater than partitioning value. Then, unless the two pointers left and right have crossed each other, we swap the two elements.

首先，我们从两个方向开始移动，找到一个反转，其中左边的一个元素不小于分区值，而右边的一个元素不大于分区值。然后，除非左右两个指针相互交叉，否则我们将这两个元素交换。

In each iteration, we move elements equal to partitioningValue towards the two ends and increment the appropriate counter:

在每个迭代中，我们将等于partitioningValue的元素向两端移动，并增加相应的计数器。

while (true) {
    while (input[left] < partitioningValue) left++; 
    
    while (input[right] > partitioningValue) {
        if (right == begin)
            break;
        right--;
    }

    if (left == right && input[left] == partitioningValue) {
        swap(input, begin + leftEqualKeysCount, left);
        leftEqualKeysCount++;
        left++;
    }

    if (left >= right) {
        break;
    }

    swap(input, left, right);

    if (input[left] == partitioningValue) {
        swap(input, begin + leftEqualKeysCount, left);
        leftEqualKeysCount++;
    }

    if (input[right] == partitioningValue) {
        swap(input, right, end - rightEqualKeysCount);
        rightEqualKeysCount++;
    }
    left++; right--;
}

In the next phase, we need to move all the equal elements from the two ends in the center. After we exit the loop, the left-pointer will be at an element whose value is not less than partitioningValue. Using this fact, we start moving equal elements from the two ends towards the center:

在下一阶段，我们需要将所有相等的元素从两端移到中间。在我们退出循环后，左指针将处于一个值不小于partitioningValue的元素处。利用这个事实，我们开始从两端向中心移动相等的元素。

right = left - 1;
for (int k = begin; k < begin + leftEqualKeysCount; k++, right--) { 
    if (right >= begin + leftEqualKeysCount)
        swap(input, k, right);
}
for (int k = end; k > end - rightEqualKeysCount; k--, left++) {
    if (left <= end - rightEqualKeysCount)
        swap(input, left, k);
}

In the last phase, we can return the boundaries of the middle partition:

在最后阶段，我们可以返回中间分区的边界。

return new Partition(right + 1, left - 1);

Finally, let’s take a look at a demonstration of our implementation on a sample input

最后，让我们看一下我们在一个样本输入上的实现演示

6. Algorithm Analysis

6.算法分析

In general, the Quicksort algorithm has an average-case time complexity of O(n*log(n)) and worst-case time complexity of O(n²). With a high density of duplicate keys, we almost always get the worst-case performance with the trivial implementation of Quicksort.

一般来说，Quicksort算法的平均时间复杂度为O(n*log(n))，最坏情况下的时间复杂度为O(n²)。在重复键密度很高的情况下，我们几乎总是能通过Quicksort的琐碎实现获得最坏情况下的性能。

However, when we use the three-way partitioning variant of Quicksort, such as DNF partitioning or Bentley’s partitioning, we’re able to prevent the negative effect of duplicate keys. Further, as the density of duplicate keys increase, the performance of our algorithm improves as well. As a result, we get the best-case performance when all keys are equal, and we get a single partition containing all equal keys in linear time.

然而，当我们使用Quicksort的三方分割变体，如DNF分割或Bentley分割时，我们就能防止重复键的负面影响。此外，随着重复键密度的增加，我们的算法的性能也在提高。因此，当所有的键都相等时，我们得到了最好的情况下的性能，我们在线性时间内得到一个包含所有相等键的单一分区。

Nevertheless, we must note that we’re essentially adding overhead when we switch to a three-way partitioning scheme from the trivial single-pivot partitioning.

尽管如此，我们必须注意到，当我们从琐碎的单支点分区切换到三支点分区方案时，我们基本上是在增加开销。

For DNF based approach, the overhead doesn’t depend on the density of repeated keys. So, if we use DNF partitioning for an array with all unique keys, then we’ll get poor performance as compared to the trivial implementation where we’re optimally choosing the pivot.

对于基于DNF的方法，开销并不取决于重复键的密度。因此，如果我们对一个具有所有唯一键的数组使用DNF分区，那么与我们优化选择枢轴的琐碎实现相比，我们会得到较差的性能。

But, Bentley-McIlroy’s approach does a smart thing as the overhead of moving the equal keys from the two extreme ends is dependent on their count. As a result, if we use this algorithm for an array with all unique keys, even then, we’ll get reasonably good performance.

但是，Bentley-McIlroy的方法做了一件很聪明的事情，因为从两个极端末端移动等价键的开销取决于它们的数量。因此，如果我们对一个拥有所有唯一键的数组使用这种算法，即使这样，我们也会得到相当好的性能。

In summary, the worst-case time complexity of both single-pivot partitioning and three-way partitioning algorithms is O(nlog(n)). However, the real benefit is visible in the best-case scenarios, where we see the time complexity going from O(nlog(n)) for single-pivot partitioning to O(n) for three-way partitioning.

综上所述，单支点分区和三向分区算法的最坏情况下的时间复杂度都是O(nlog(n))。然而，真正的好处在最佳情况下是可见的，我们看到时间复杂度从单枢纽分区的O(nlog(n))到三向分区的O(n)。

7. Conclusion

7.结语

In this tutorial, we learned about the performance issues with the trivial implementation of the Quicksort algorithm when the input has a large number of repeated elements.

在本教程中，我们了解了当输入有大量的重复元素时，Quicksort算法的琐碎实现的性能问题。

With a motivation to fix this issue, we learned different three-way partitioning schemes and how we can implement them in Java.

带着解决这个问题的动机，我们学习了不同的三方分区方案以及如何在Java中实现它们。

As always, the complete source code for the Java implementation used in this article is available on GitHub.

一如既往，本文中使用的Java实现的完整源代码可在GitHub上获得。