1. Overview
1.概述
In this tutorial, we’ll take a look at the Java implementation of Boruvka’s algorithm for finding a Minimum Spanning Tree (MST) of an edge-weighted graph.
在本教程中,我们将看一下Boruvka算法的Java实现,该算法用于寻找边加权图的最小生成树(MST)。
It predates Prim’s and Kruskal’s algorithms, but still can be considered a cross between the two.
它比Prim的算法和Kruskal的算法要早,但仍然可以认为是两者的交叉。
2. Boruvka’s Algorithm
2.博鲁夫卡的算法
We’ll jump right into the algorithm at hand. Let’s look at a bit of history and then the algorithm itself.
我们将直接跳入手头的算法。让我们先看一下历史,然后看一下算法本身。
2.1. History
2.1.历史
A way to find an MST of a given graph was first formulated by Otakar Boruvka in 1926. This was way before computers even existed, and was in fact modeled to design an efficient electricity distribution system.
找到给定图形的MST的方法是由Otakar Boruvka在1926年首次提出的。这是在计算机出现之前的事情,实际上是为了设计一个高效的电力分配系统而建立的模型。
Georges Sollin rediscovered it in 1965 and used it in parallel computing.
乔治-索林在1965年重新发现了它,并将其用于并行计算。
2.2. The Algorithm
2.2.算法
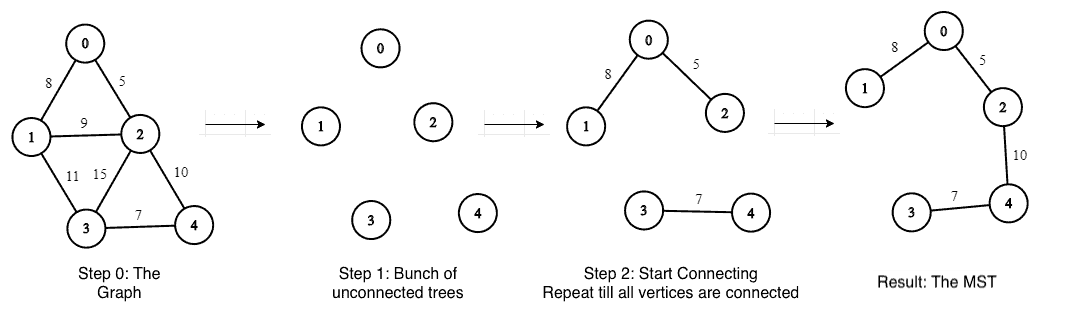
The central idea of the algorithm is to start with a bunch of trees with each vertex representing an isolated tree. Then, we need to keep adding edges to reduce the number of isolated trees until we have a single connected tree.
该算法的中心思想是以一堆树开始,每个顶点代表一棵孤立的树。然后,我们需要不断添加边来减少孤立树的数量,直到我们有一棵连接的树。
Let’s see this in steps with an example graph:
让我们通过一个例子图来看看这个步骤。
- Step 0: create a graph
- Step 1: start with a bunch of unconnected trees (number of trees = number of vertices)
- Step 2: while there are unconnected trees, for each unconnected tree:
- find its edge with lesser weight
- add this edge to connect another tree
3. Java Implementation
3.java实现
Now let’s see how we can implement this in Java.
现在让我们看看如何在Java中实现这一点。
3.1. The UnionFind Data Structure
3.1.UnionFind数据结构
To start with, we need a data structure to store the parents and ranks of our vertices.
首先,我们需要一个数据结构来存储我们顶点的父辈和等级。
Let’s define a class UnionFind for this purpose, with two methods: union, and find:
让我们为此定义一个UnionFind类,有两个方法。union, 和find。
public class UnionFind {
private int[] parents;
private int[] ranks;
public UnionFind(int n) {
parents = new int[n];
ranks = new int[n];
for (int i = 0; i < n; i++) {
parents[i] = i;
ranks[i] = 0;
}
}
public int find(int u) {
while (u != parents[u]) {
u = parents[u];
}
return u;
}
public void union(int u, int v) {
int uParent = find(u);
int vParent = find(v);
if (uParent == vParent) {
return;
}
if (ranks[uParent] < ranks[vParent]) {
parents[uParent] = vParent;
} else if (ranks[uParent] > ranks[vParent]) {
parents[vParent] = uParent;
} else {
parents[vParent] = uParent;
ranks[uParent]++;
}
}
}
We may think of this class as a helper structure for maintaining relationships between our vertices and gradually building up our MST.
我们可以把这个类看作是维护顶点之间关系的辅助结构,并逐渐建立起我们的MST。
To find out whether two vertices u and v belong to the same tree, we see if find(u) returns the same parent as find(v). The union method is used to combine trees. We’ll see this usage shortly.
要找出两个顶点u和v是否属于同一棵树,我们要看find(u)是否与find(v)返回同一个父节点。union方法被用来组合树。我们很快就会看到这种用法。
3.2. Input a Graph From the User
3.2.从用户那里输入一个图形
Now we need a way to get a graph’s vertices and edges from the user and map them to objects we can use in our algorithm at runtime.
现在我们需要一种方法来从用户那里获得图形的顶点和边,并将它们映射为我们在运行时可以在算法中使用的对象。
Since we’ll use JUnit to test out our algorithm, this part goes in a @Before method:
由于我们将使用JUnit来测试我们的算法,这部分将放在@Before方法中。
@Before
public void setup() {
graph = ValueGraphBuilder.undirected().build();
graph.putEdgeValue(0, 1, 8);
graph.putEdgeValue(0, 2, 5);
graph.putEdgeValue(1, 2, 9);
graph.putEdgeValue(1, 3, 11);
graph.putEdgeValue(2, 3, 15);
graph.putEdgeValue(2, 4, 10);
graph.putEdgeValue(3, 4, 7);
}
Here, we’ve used Guava’s MutableValueGraph<Integer, Integer> to store our graph. Then we used ValueGraphBuilder to construct an undirected weighted graph.
在这里,我们使用Guava的MutableValueGraph<Integer, Integer>来存储我们的图。然后我们使用ValueGraphBuilder来构建一个无向加权图。
The method putEdgeValue takes three arguments, two Integers for the vertices, and the third Integer for its weight, as specified by MutableValueGraph‘s generic type declaration.
方法putEdgeValue需要三个参数,两个Integer代表顶点,第三个Integer代表其权重,正如MutableValueGraph的通用类型声明所指定的。
As we can see, this is the same input as shown in our diagram from earlier.
正如我们所看到的,这与我们之前的图表中显示的输入相同。
3.3. Derive Minimum Spanning Tree
3.3.推导出最小生成树
Finally, we come to the crux of the matter, the implementation of the algorithm.
最后,我们来到了问题的关键,即算法的实施。
We’ll do this in a class we’ll call BoruvkaMST. First, let’s declare a couple of instance variables:
我们将在一个名为BoruvkaMST的类中完成这一工作。首先,让我们声明几个实例变量。
public class BoruvkaMST {
private static MutableValueGraph<Integer, Integer> mst = ValueGraphBuilder.undirected().build();
private static int totalWeight;
}
As we can see, we are making use of MutableValueGraph<Integer, Integer> here to represent the MST.
我们可以看到,我们在这里利用MutableValueGraph<Integer, Integer>来表示MST。
Second, we’ll define a constructor, where all the magic happens. It takes one argument – the graph we built earlier.
其次,我们将定义一个构造函数,所有的魔法都在这里发生。它需要一个参数–我们之前构建的graph。
The first thing it does is to initialize a UnionFind of the input graph’s vertices. Initially, all vertices are their own parents, each with a rank of 0:
它做的第一件事是初始化输入图的顶点的UnionFind。 最初,所有顶点都是它们自己的父辈,每个顶点的等级为0。
public BoruvkaMST(MutableValueGraph<Integer, Integer> graph) {
int size = graph.nodes().size();
UnionFind uf = new UnionFind(size);
Next, we’ll create a loop that defines the number of iterations required to create the MST – at most log V times or until we have V-1 edges, where V is the number of vertices:
接下来,我们将创建一个循环,定义创建MST所需的迭代次数–最多对数V次或直到我们有V-1条边,其中V是顶点的数量。
for (int t = 1; t < size && mst.edges().size() < size - 1; t = t + t) {
EndpointPair<Integer>[] closestEdgeArray = new EndpointPair[size];
Here we also initialize an array of edges, closestEdgeArray – to store the closest, lesser-weighted edges.
这里我们也初始化了一个边缘数组,closestEdgeArray – 来存储最接近的、权重较低的边缘。
After that, we’ll define an inner for loop to iterate over all the edges of the graph to populate our closestEdgeArray.
之后,我们将定义一个内部for循环,遍历图形的所有边,以填充我们的closestEdgeArray。
If the parents of the two vertices are the same, it’s the same tree and we don’t add it to the array. Otherwise, we compare the current edge’s weight to the weight of its parent vertices’ edges. If it’s lesser, then we add it to closestEdgeArray:
如果两个顶点的父顶点是一样的,那就是同一棵树,我们就不把它加到数组中。否则,我们将当前边的权重与它的父顶点的边的权重进行比较。如果它较小,那么我们就把它添加到closestEdgeArray:。
for (EndpointPair<Integer> edge : graph.edges()) {
int u = edge.nodeU();
int v = edge.nodeV();
int uParent = uf.find(u);
int vParent = uf.find(v);
if (uParent == vParent) {
continue;
}
int weight = graph.edgeValueOrDefault(u, v, 0);
if (closestEdgeArray[uParent] == null) {
closestEdgeArray[uParent] = edge;
}
if (closestEdgeArray[vParent] == null) {
closestEdgeArray[vParent] = edge;
}
int uParentWeight = graph.edgeValueOrDefault(closestEdgeArray[uParent].nodeU(),
closestEdgeArray[uParent].nodeV(), 0);
int vParentWeight = graph.edgeValueOrDefault(closestEdgeArray[vParent].nodeU(),
closestEdgeArray[vParent].nodeV(), 0);
if (weight < uParentWeight) {
closestEdgeArray[uParent] = edge;
}
if (weight < vParentWeight) {
closestEdgeArray[vParent] = edge;
}
}
Then, we’ll define a second inner loop to create a tree. We’ll add edges from the above step to this tree without adding the same edge twice. Additionally, we’ll perform a union on our UnionFind to derive and store parents and ranks of the newly created trees’ vertices:
然后,我们将定义第二个内循环来创建一棵树。我们将把上述步骤中的边添加到这棵树上,而不会把同一个边添加两次。此外,我们将对我们的UnionFind执行一个union,以得出并存储新创建的树的顶点的父级和等级。
for (int i = 0; i < size; i++) {
EndpointPair<Integer> edge = closestEdgeArray[i];
if (edge != null) {
int u = edge.nodeU();
int v = edge.nodeV();
int weight = graph.edgeValueOrDefault(u, v, 0);
if (uf.find(u) != uf.find(v)) {
mst.putEdgeValue(u, v, weight);
totalWeight += weight;
uf.union(u, v);
}
}
}
After repeating these steps at most log V times or until we have V-1 edges, the resulting tree is our MST.
在重复这些步骤最多对数V次或直到我们有V-1条边之后,得到的树就是我们的MST。
4. Testing
4.测试
Finally, let’s see a simple JUnit to verify our implementation:
最后,让我们看看一个简单的JUnit来验证我们的实现。
@Test
public void givenInputGraph_whenBoruvkaPerformed_thenMinimumSpanningTree() {
BoruvkaMST boruvkaMST = new BoruvkaMST(graph);
MutableValueGraph<Integer, Integer> mst = boruvkaMST.getMST();
assertEquals(30, boruvkaMST.getTotalWeight());
assertEquals(4, mst.getEdgeCount());
}
As we can see, we got the MST with a weight of 30 and 4 edges, the same as the pictorial example.
我们可以看到,我们得到的MST的权重为30,有4条边,与图例相同。
5. Conclusion
5.总结
In this tutorial, we saw the Java implementation of the Boruvka Algorithm. Its time complexity is O(E log V), where E is the number of edges and V is the number of vertices.
在本教程中,我们看到了Boruvka算法的Java实现。其时间复杂度为O(E log V),其中E为边的数量,V为顶点的数量。
As always, source code is available over on GitHub.
一如既往,源代码可以在GitHub上获得。