1. Overview
1.概述
In a previous article, we introduced Prim’s algorithm to find the minimum spanning trees. In this article, we’ll use another approach, Kruskal’s algorithm, to solve the minimum and maximum spanning tree problems.
在前一篇文章中,我们介绍了Prim的算法来寻找最小生成树。在这篇文章中,我们将使用另一种方法,即Kruskal算法,来解决最小和最大生成树问题。
2. Spanning Tree
2.生成树
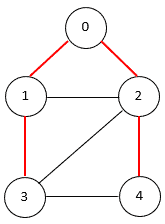
A spanning tree of an undirected graph is a connected subgraph that covers all the graph nodes with the minimum possible number of edges. In general, a graph may have more than one spanning tree. The following figure shows a graph with a spanning tree (edges of the spanning tree are in red):
无向图的生成树是一个连接子图,它以尽可能少的边数覆盖所有的图节点。一般来说,一个图可能有不止一棵生成树。下图显示了一个有生成树的图形(生成树的边为红色)。
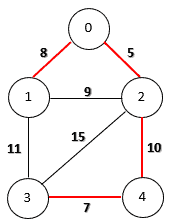
If the graph is edge-weighted, we can define the weight of a spanning tree as the sum of the weights of all its edges. A minimum spanning tree is a spanning tree whose weight is the smallest among all possible spanning trees. The following figure shows a minimum spanning tree on an edge-weighted graph:
如果图是边加权的,我们可以将生成树的权重定义为其所有边的权重之和。最小生成树是指其权重在所有可能的生成树中最小的生成树。下图显示了一个边加权图上的最小生成树。
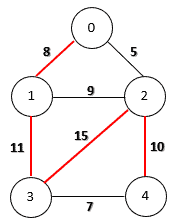
Similarly, a maximum spanning tree has the largest weight among all spanning trees. The following figure shows a maximum spanning tree on an edge-weighted graph:
同样地,最大生成树在所有生成树中具有最大的权重。下图显示了一个边加权图上的最大生成树。
3. Kruskal’s Algorithm
3 克鲁斯卡的算法
Given a graph, we can use Kruskal’s algorithm to find its minimum spanning tree. If the number of nodes in a graph is V, then each of its spanning trees should have (V-1) edges and contain no cycles. We can describe Kruskal’s algorithm in the following pseudo-code:
给定一个图,我们可以用Kruskal的算法来寻找它的最小生成树。如果一个图的节点数是V,那么它的每一棵生成树都应该有(V-1)条边,并且不包含循环。我们可以用下面的伪代码来描述Kruskal的算法。
Initialize an empty edge set T.
Sort all graph edges by the ascending order of their weight values.
foreach edge in the sorted edge list
Check whether it will create a cycle with the edges inside T.
If the edge doesn't introduce any cycles, add it into T.
If T has (V-1) edges, exit the loop.
return TLet’s run Kruskal’s algorithm for a minimum spanning tree on our sample graph step-by-step:
让我们在我们的样本图上逐步运行Kruskal的最小生成树的算法。
Firstly, we choose the edge (0, 2) because it has the smallest weight. Then, we can add edges (3, 4) and (0, 1) as they do not create any cycles. Now the next candidate is edge (1, 2) with weight 9. However, if we include this edge, we’ll produce a cycle (0, 1, 2). Therefore, we discard this edge and continue to choose the next smallest one. Finally, the algorithm finishes by adding the edge (2, 4) of weight 10.
首先,我们选择边(0,2),因为它具有最小的权重。然后,我们可以添加边(3,4)和(0,1),因为它们不会产生任何循环。现在,下一个候选边是权重为9的边(1,2)。然而,如果我们加入这条边,我们将产生一个循环(0,1,2)。因此,我们放弃这条边,继续选择下一条最小的边。最后,该算法通过添加权重为10的边(2,4)来完成。
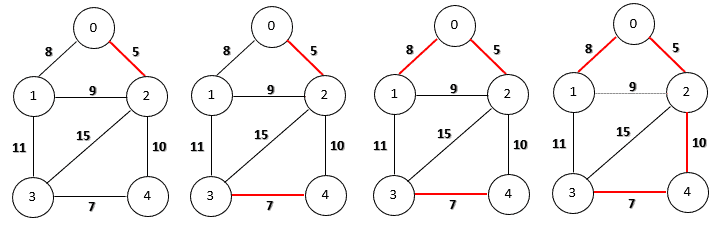
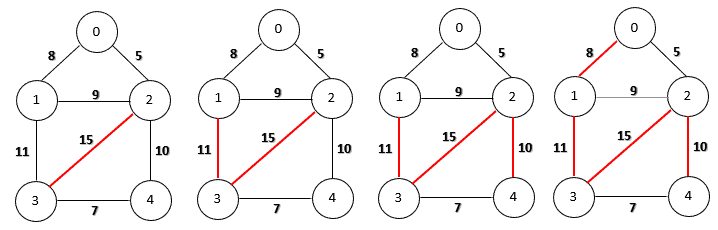
To calculate the maximum spanning tree, we can change the sorting order to descending order. The other steps remain the same. The following figure shows the step-by-step construction of a maximum spanning tree on our sample graph.
为了计算最大生成树,我们可以将排序顺序改为降序。其他步骤保持不变。下图显示了在我们的样本图上一步步构建最大生成树的过程。
4. Cycle Detection with a Disjoint Set
4.循环检测与不相交集
In Kruskal’s algorithm, the crucial part is to check whether an edge will create a cycle if we add it to the existing edge set. There are several graph cycle detection algorithms we can use. For example, we can use a depth-first search (DFS) algorithm to traverse the graph and detect whether there is a cycle.
在Kruskal的算法中,关键的部分是检查一条边是否会产生一个循环,如果我们把它添加到现有的边集上。我们可以使用几种图形循环检测算法。例如,我们可以使用深度优先搜索(DFS)算法来遍历图形并检测是否存在周期。
However, we need to do a cycle detection on existing edges each time when we test a new edge. A faster solution is to use the Union-Find algorithm with the disjoint data structure because it also uses an incremental edge adding approach to detect cycles. We can fit this into our spanning tree construction process.
然而,我们需要在每次测试新边时对现有边进行循环检测。一个更快的解决方案是使用Union-Find算法与disjoint数据结构,因为它也 使用增量的边添加方法来检测周期。我们可以将其纳入我们的生成树构建过程。
4.1. Disjoint Set and Spanning Tree Construction
4.1.交叉集和生成树的构建
Firstly, we treat each node of the graph as an individual set that contains only one node. Then, each time we introduce an edge, we check whether its two nodes are in the same set. If the answer is yes, then it will create a cycle. Otherwise, we merge the two disjoint sets into one set and include the edge for the spanning tree.
首先,我们将图中的每个节点视为一个单独的集合,只包含一个节点。然后,每次我们引入一条边时,我们检查它的两个节点是否在同一个集合中。如果答案是肯定的,那么它将创建一个循环。否则,我们将这两个互不相干的集合合并为一个集合,并包括生成树的边。
We can repeat the above steps until we construct the whole spanning tree.
我们可以重复上述步骤,直到我们构建整个生成树。
For example, in the above minimum spanning tree construction, we first have 5 node sets: {0}, {1}, {2}, {3}, {4}. When we check the first edge (0, 2), its two nodes are in different node sets. Therefore, we can include this edge and merge {0} and {2} into one set {0, 2}.
例如,在上述最小生成树构建中,我们首先有5个节点集。{0}, {1}, {2}, {3}, {4}.当我们检查第一条边(0,2)时,它的两个节点在不同的节点集中。因此,我们可以包括这条边,并将{0}和{2}合并为一个集合{0,2}。
We can do similar operations for the edges (3, 4) and (0, 1). The node sets then become {0, 1, 2} and {3, 4}. When we check the next edge (1, 2), we can see that both nodes of this edge are in the same set. Therefore, we discard this edge and continue to check the next one. Finally, the edge (2, 4) satisfies our condition, and we can include it for the minimum spanning tree.
我们可以对边(3,4)和(0,1)做类似的操作。节点集就变成了{0,1,2}和{3,4}。当我们检查下一条边(1,2)时,我们可以看到这条边的两个节点都在同一个集合中。因此,我们放弃这条边,继续检查下一条。最后,边(2,4)满足了我们的条件,我们可以把它纳入最小生成树中。
4.2. Disjoint Set Implementation
4.2.交叉集的实现
We can use a tree structure to represent a disjoint set. Each node has a parent pointer to reference its parent node. In each set, there is a unique root node that represents this set. The root node has a self-referenced parent pointer.
我们可以用一个树形结构来表示一个不相交的集合。每个节点都有一个parent指针来引用其父节点。在每个集合中,有一个唯一的根节点,代表这个集合。根节点有一个自我引用的parent指针。
Let’s use a Java class to define the disjoint set information:
让我们用一个Java类来定义不相交集的信息。
public class DisjointSetInfo {
private Integer parentNode;
DisjointSetInfo(Integer parent) {
setParentNode(parent);
}
//standard setters and getters
}Let’s label each graph node with an integer number, starting from 0. We can use a list data structure, List<DisjointSetInfo> nodes, to store the disjoint set information of a graph. In the beginning, each node is the representative member of its own set:
我们可以使用一个列表数据结构,List<DisjointSetInfo>nodes,来存储图的不相干集合信息。在开始时,每个节点都是它自己集合的代表成员。
void initDisjointSets(int totalNodes) {
nodes = new ArrayList<>(totalNodes);
for (int i = 0; i < totalNodes; i++) {
nodes.add(new DisjointSetInfo(i));
}
}
4.3. Find Operation
4.3 查找操作
To find the set that a node belongs to, we can follow the node’s parent chain upwards until we reach the root node:
为了找到一个节点所属的集合,我们可以沿着该节点的父链往上走,直到到达根节点。
Integer find(Integer node) {
Integer parent = nodes.get(node).getParentNode();
if (parent.equals(node)) {
return node;
} else {
return find(parent);
}
}It is possible to have a highly unbalanced tree structure for a disjoint set. We can improve the find operation by using the path compression technique.
对于一个不相交集来说,有可能出现一个高度不平衡的树状结构。我们可以通过使用path压缩技术来改善find操作。
Since each node we visit on the way to the root node is part of the same set, we can attach the root node to its parent reference directly. The next time when we visit this node, we need one lookup path to get the root node:
由于我们在通往根节点的路上所访问的每个节点都是同一个集合的一部分,我们可以直接将根节点附加到其parent reference上。下次当我们访问这个节点时,我们需要一个查找路径来获得根节点。
Integer pathCompressionFind(Integer node) {
DisjointSetInfo setInfo = nodes.get(node);
Integer parent = setInfo.getParentNode();
if (parent.equals(node)) {
return node;
} else {
Integer parentNode = find(parent);
setInfo.setParentNode(parentNode);
return parentNode;
}
}4.4. Union Operation
4.4.联盟运作
If the two nodes of an edge are in different sets, we’ll combine these two sets into one. We can achieve this union operation by setting the root of one representative node to the other representative node:
如果一条边的两个节点在不同的集合中,我们将把这两个集合合并成一个。我们可以通过将一个代表节点的根设置为另一个代表节点来实现这个union操作。
void union(Integer rootU, Integer rootV) {
DisjointSetInfo setInfoU = nodes.get(rootU);
setInfoU.setParentNode(rootV);
}This simple union operation could produce a highly unbalanced tree as we chose a random root node for the merged set. We can improve the performance using a union by rank technique.
这种简单的联合操作可能会产生一个非常不平衡的树,因为我们为合并后的集合随机选择了一个根节点。我们可以使用按等级联合技术来提高性能。
Since it is tree depth that affects the running time of the find operation, we attach the set with the shorter tree to the set with the longer tree. This technique only increases the depth of the merged tree if the original two trees have the same depth.
由于影响查找操作的运行时间的是树的深度,我们将具有较短树的集合附加到具有较长树的集合。这种技术只在原始的两棵树具有相同深度的情况下增加合并后的树的深度。
To achieve this, we first add a rank property to the DisjointSetInfo class:
为了实现这一点,我们首先向DisjointSetInfo类添加一个rank属性。
public class DisjointSetInfo {
private Integer parentNode;
private int rank;
DisjointSetInfo(Integer parent) {
setParentNode(parent);
setRank(0);
}
//standard setters and getters
}In the beginning, a single node disjoint has a rank of 0. During the union of two sets, the root node with a higher rank becomes the root node of the merged set. We increase the new root node’s rank by one only if the original two ranks are the same:
在开始的时候,一个单节点disjoint的等级是0。在两个集合的合并过程中,等级较高的根节点成为合并后的集合的根节点。只有在原来的两个等级相同的情况下,我们才将新的根节点的等级增加1。
void unionByRank(int rootU, int rootV) {
DisjointSetInfo setInfoU = nodes.get(rootU);
DisjointSetInfo setInfoV = nodes.get(rootV);
int rankU = setInfoU.getRank();
int rankV = setInfoV.getRank();
if (rankU < rankV) {
setInfoU.setParentNode(rootV);
} else {
setInfoV.setParentNode(rootU);
if (rankU == rankV) {
setInfoU.setRank(rankU + 1);
}
}
}4.5. Cycle Detection
4.5.循环检测
We can determine whether two nodes are in the same disjoint set by comparing the results of two find operations. If they have the same representive root node, then we’ve detected a cycle. Otherwise, we merge the two disjoint sets by using a union operation:
我们可以通过比较两个find操作的结果来确定两个节点是否在同一个不相交集中。如果它们有相同的代表根节点,那么我们就发现了一个循环。否则,我们通过使用union操作来合并这两个不相干的集合。
boolean detectCycle(Integer u, Integer v) {
Integer rootU = pathCompressionFind(u);
Integer rootV = pathCompressionFind(v);
if (rootU.equals(rootV)) {
return true;
}
unionByRank(rootU, rootV);
return false;
}
The cycle detection, with the union by rank technique alone, has a running time of O(logV). We can achieve better performance with both path compression and union by rank techniques. The running time is O(α(V)), where α(V) is the inverse Ackermann function of the total number of nodes. It is a small constant that is less than 5 in our real-world computations.
单独使用union by rank技术进行周期检测,的运行时间为O(logV)。我们可以通过路径压缩和按等级合并技术实现更好的性能。运行时间是 O(α(V)),其中α(V)是节点总数的逆Ackermann函数。它是一个小常数,在我们的实际计算中小于5。
5. Java Implementation of Kruskal’s Algorithm
5.克鲁斯克算法的Java实现
We can use the ValueGraph data structure in Google Guava to represent an edge-weighted graph.
我们可以使用ValueGraph中的数据结构来表示一个边加权图。
To use ValueGraph, we first need to add the Guava dependency to our project’s pom.xml file:
要使用ValueGraph,我们首先需要将Guava依赖性添加到我们项目的pom.xml文件中。
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>31.0.1-jre</version>
</dependency>We can wrap the above cycle detection methods into a CycleDetector class and use it in Kruskal’s algorithm. Since the minimum and maximum spanning tree construction algorithms only have a slight difference, we can use one general function to achieve both constructions:
我们可以将上述周期检测方法包装成一个CycleDetector类,并在Kruskal的算法中使用它。由于最小生成树和最大生成树的构造算法只有微小的差别,我们可以使用一个通用函数来实现这两种构造。
ValueGraph<Integer, Double> spanningTree(ValueGraph<Integer, Double> graph, boolean minSpanningTree) {
Set<EndpointPair> edges = graph.edges();
List<EndpointPair> edgeList = new ArrayList<>(edges);
if (minSpanningTree) {
edgeList.sort(Comparator.comparing(e -> graph.edgeValue(e).get()));
} else {
edgeList.sort(Collections.reverseOrder(Comparator.comparing(e -> graph.edgeValue(e).get())));
}
int totalNodes = graph.nodes().size();
CycleDetector cycleDetector = new CycleDetector(totalNodes);
int edgeCount = 0;
MutableValueGraph<Integer, Double> spanningTree = ValueGraphBuilder.undirected().build();
for (EndpointPair edge : edgeList) {
if (cycleDetector.detectCycle(edge.nodeU(), edge.nodeV())) {
continue;
}
spanningTree.putEdgeValue(edge.nodeU(), edge.nodeV(), graph.edgeValue(edge).get());
edgeCount++;
if (edgeCount == totalNodes - 1) {
break;
}
}
return spanningTree;
}In Kruskal’s algorithm, we first sort all graph edges by their weights. This operation takes O(ElogE) time, where E is the total number of edges.
在Kruskal的算法中,我们首先按权重对所有图的边进行排序。这个操作需要O(ElogE)时间,其中E是边的总数。
Then we use a loop to go through the sorted edge list. In each iteration, we check whether a cycle will be formed by adding the edge into the current spanning tree edge set. This loop with the cycle detection takes at most O(ElogV) time.
然后,我们使用一个循环来浏览排序后的边缘列表。在每次迭代中,我们通过将边缘加入当前生成树边缘集来检查是否会形成一个循环。这个带有循环检测的循环最多需要O(ElogV) 时间。
Therefore, the overall running time is O(ELogE + ELogV). Since the value of E is in the scale of O(V2), the time complexity of Kruskal’s algorithm is O(ElogE) or O(ElogV).
因此,总体运行时间是O(ELogE+ELogV)。由于E的值在O(V2)的范围内,Kruskal算法的时间复杂性是O(ElogE)或O(ElogV)。
6. Conclusion
6.结语
In this article, we learned how to use Kruskal’s algorithm to find a minimum or maximum spanning tree of a graph. As always, the source code for the article is available over on GitHub.
在这篇文章中,我们学习了如何使用Kruskal的算法来寻找图的最小或最大生成树。像往常一样,本文的源代码可在GitHub上获得。