1. Overview

1.概述

In this quick tutorial, we’ll learn how we can detect a cycle in a given directed graph.

在这个快速教程中，我们将学习如何在给定的有向图中检测一个周期。

2. Graph Representation

2.图形表示法

For this tutorial, we’ll stick with the adjacency list graph representation.

在本教程中，我们将坚持使用邻接列表graph representation。

Firstly, let’s start by defining a Vertex in Java:

首先，让我们先在Java中定义一个Vertex。

public class Vertex {

    private String label;
    private boolean beingVisited;
    private boolean visited;
    private List<Vertex> adjacencyList;

    public Vertex(String label) {
        this.label = label;
        this.adjacencyList = new ArrayList<>();
    }

    public void addNeighbor(Vertex adjacent) {
        this.adjacencyList.add(adjacent);
    }
    //getters and setters
}

Here, the adjacencyList of a vertex v holds a list of all vertices adjacent to v. The addNeighbor() method adds a neighboring vertex to the adjacency list of v.

在这里，顶点的adjacencyList持有与v相邻的所有顶点的列表。 addNeighbor()方法将一个相邻的顶点添加到v的邻接列表。

We’ve also defined two boolean parameters, beingVisited and visited, which represent whether the node is currently being visited or has already been visited.

我们还定义了两个boolean参数，beingVisited和visited，它们代表节点是否正在被访问或已经被访问。

A graph can be thought of as a group of vertices or nodes connected through the edges.

一个图可以被认为是一组通过边连接的顶点或节点。

So, let’s now quickly represent a Graph in Java:

所以，现在让我们在Java中快速表示一个Graph。

public class Graph {

    private List<Vertex> vertices;

    public Graph() {
        this.vertices = new ArrayList<>();
    }

    public void addVertex(Vertex vertex) {
        this.vertices.add(vertex);
    }

    public void addEdge(Vertex from, Vertex to) {
        from.addNeighbor(to);
    }

   // ...
}

We’ll use the addVertex() and addEdge() methods to add new vertices and edges in our graph.

我们将使用addVertex()和addEdge()方法来在我们的图中添加新的顶点和边。

3. Cycle Detection

3.循环检测

To detect a cycle in a directed graph, we’ll use a variation of DFS traversal:

为了检测有向图中的循环，我们将使用DFS遍历的一个变体：。

Pick up an unvisited vertex v and mark its state as beingVisited
For each neighboring vertex u of v, check:
- If u is already in the beingVisited state, it clearly means there exists a backward edge and so a cycle has been detected
- If u is yet in an unvisited state, we’ll recursively visit u in a depth-first manner
Update the vertex v‘s beingVisited flag to false and its visited flag to true

Note that all the vertices of our graph are initially in an unvisited state as both their beingVisited and visited flags are initialized with false.

请注意，我们图中的所有顶点最初都处于未访问状态，因为它们的beingVisited和visited标志都被初始化为false。

Let’s now look at our Java solution:

现在让我们来看看我们的Java解决方案。

public boolean hasCycle(Vertex sourceVertex) {
    sourceVertex.setBeingVisited(true);

    for (Vertex neighbor : sourceVertex.getAdjacencyList()) {
        if (neighbor.isBeingVisited()) {
            // backward edge exists
            return true;
        } else if (!neighbor.isVisited() && hasCycle(neighbor)) {
            return true;
        }
    }

    sourceVertex.setBeingVisited(false);
    sourceVertex.setVisited(true);
    return false;
}

We can use any vertex in a graph to be the source or the starting vertex.

我们可以使用图中的任何顶点作为源点或起始顶点。

For a disconnected graph, we’ll have to add an additional wrapper method:

对于断开连接的图，我们必须添加一个额外的封装方法：。

public boolean hasCycle() {
    for (Vertex vertex : vertices) {
        if (!vertex.isVisited() && hasCycle(vertex)) {
            return true;
        }
    }
    return false;
}

This is to ensure that we visit every component of a disconnected graph for detecting a cycle.

这是为了确保我们在检测周期时访问不连接图的每一个组件。

4. Implementation Testing

4.实施测试

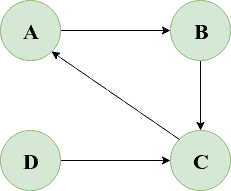
Let’s consider the below cyclic directed graph:

让我们考虑下面这个循环有向图。

We can quickly write a JUnit to verify our hasCycle() method for this graph:

我们可以快速编写一个JUnit来验证我们的hasCycle()方法对这个图的作用。

@Test
public void givenGraph_whenCycleExists_thenReturnTrue() {

    Vertex vertexA = new Vertex("A");
    Vertex vertexB = new Vertex("B");
    Vertex vertexC = new Vertex("C")
    Vertex vertexD = new Vertex("D");

    Graph graph = new Graph();
    graph.addVertex(vertexA);
    graph.addVertex(vertexB);
    graph.addVertex(vertexC);
    graph.addVertex(vertexD);

    graph.addEdge(vertexA, vertexB);
    graph.addEdge(vertexB, vertexC);
    graph.addEdge(vertexC, vertexA);
    graph.addEdge(vertexD, vertexC);

    assertTrue(graph.hasCycle());

}

Here, our hasCycle() method returned true denoting that our graph is cyclic.

这里，我们的hasCycle()方法返回true，表示我们的图是循环的。

5. Conclusion

5.总结

In this tutorial, we learned how to check if a cycle exists in a given directed graph in Java.

在本教程中，我们学习了如何在Java中检查一个给定的有向图中是否存在一个周期。

As usual, the code implementation with examples is available over on Github.

像往常一样，带有示例的代码实现可在Github上获得。