1. Overview
1.概述
In this tutorial, we’ll look at the basic concepts of a graph as a data structure.
在本教程中,我们将了解图作为一种数据结构的基本概念。
We’ll also explore its implementation in Java along with various operations possible on a graph. We will also discuss the Java libraries offering graph implementations.
我们还将探讨它在Java中的实现,以及在图上可能的各种操作。我们还将讨论提供图形实现的Java库。
2. Graph Data Structure
2.图表数据结构
A graph is a data structure for storing connected data such as a network of people on a social media platform.
图是一种数据结构,用于存储连接的数据,如社交媒体平台上的人际网络。
A graph consists of vertices and edges. A vertex represents the entity (e.g., people) and an edge represents the relationship between entities (e.g., a person’s friendships).
一个图由顶点和边组成。一个顶点代表实体(例如,人),一条边代表实体之间的关系(例如,一个人的友谊)。
Let’s define a simple Graph to understand this better:
让我们定义一个简单的图表来更好地理解这一点。
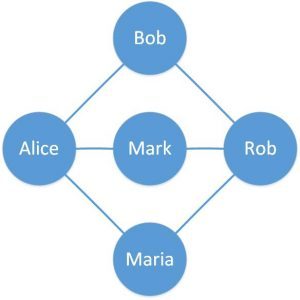
Here we’ve defined a simple graph with five vertices and six edges. The circles are vertices representing people and the lines connecting two vertices are edges representing friends on an online portal.
这里我们定义了一个有五个顶点和六条边的简单图形。圆圈是代表人的顶点,连接两个顶点的线是代表在线门户的朋友的边。
There are a few variations of this simple graph depending on the properties of the edges. Let’s briefly go through them in the next sections.
根据边的属性,这个简单的图有一些变化。让我们在接下来的章节中简单介绍一下。
However, we’ll only focus on the simple graph presented here for the Java examples in this tutorial.
然而,在本教程的Java例子中,我们将只关注这里介绍的简单图形。
2.1. Directed Graph
2.1.有向图
The graph we’ve defined so far has edges without any direction. If these edges feature a direction in them, the resulting graph is known as a directed graph.
到目前为止,我们所定义的图有没有任何方向的边。如果这些边具有方向性,那么产生的图就被称为directed graph。
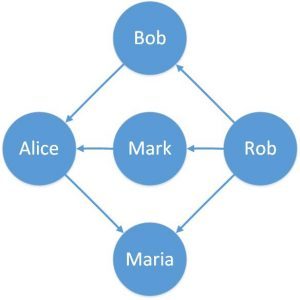
An example of this can be representing who sent the friend request in a friendship on the online portal:
这方面的一个例子可以代表谁在网上门户的友谊中发出了朋友请求。
Here we can see that the edges have a fixed direction. The edges can be bidirectional as well.
在这里我们可以看到,边缘有一个固定的方向。边缘也可以是双向的。
2.2. Weighted Graph
2.2.加权图
Again, our simple graph has edges that are unbiased or unweighted.
同样,我们的简单图的边是无偏的或无权的。
If instead these edges carry relative weight, this graph is known as a weighted graph.
如果这些边带有相对的权重,这个图就被称为加权图。
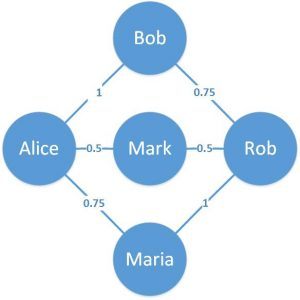
An example of a practical application of this can be representing how relatively old a friendship is on the online portal:
这方面的一个实际应用的例子可以是代表在线门户上的友谊有多大。
Here we can see that the edges have weights associated with them. This provides a relative meaning to these edges.
在这里我们可以看到,这些边有与之相关的权重。这为这些边提供了一个相对的意义。
3. Graph Representations
3.图形表示法
A graph can be represented in different forms such as adjacency matrix and adjacency list. Each one has their pros and cons in a different setup.
图可以用不同的形式表示,如邻接矩阵和邻接列表。在不同的设置中,每一种都有其优点和缺点。
We’ll introduce these graph representations in this section.
我们将在本节中介绍这些图的表示方法。
3.1. Adjacency Matrix
3.1.邻接矩阵
An adjacency matrix is a square matrix with dimensions equivalent to the number of vertices in the graph.
邻接矩阵是一个尺寸相当于图中顶点数量的方形矩阵。
The elements of the matrix typically have values 0 or 1. A value of 1 indicates adjacency between the vertices in the row and column and a value of 0 otherwise.
矩阵的元素通常有0或1的值。值为1表示该行和该列的顶点之间相邻,否则值为0。
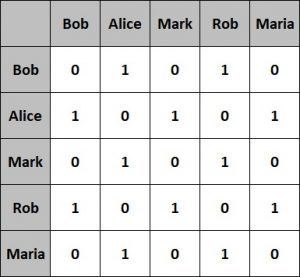
Let’s see what the adjacency matrix looks like for our simple graph from the previous section:
让我们看看上一节中我们的简单图的邻接矩阵是什么样子的。
This representation is fairly easier to implement and efficient to query as well. However, it’s less efficient with respect to space occupied.
这种表示法在实现上相当容易,在查询上也很高效。然而,在占用空间方面,它的效率较低。
3.2. Adjacency List
3.2.邻接列表
An adjacency list is nothing but an array of lists. The size of the array is equivalent to the number of vertices in the graph.
一个邻接列表只不过是一个列表的数组。数组的大小相当于图中顶点的数量。
The list at a specific index of the array represents the adjacent vertices of the vertex represented by that array index.
数组中某一特定索引的列表代表该数组索引所代表的顶点的相邻顶点。
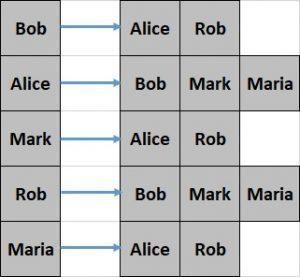
Let’s see what the adjacency list looks like for our simple graph from the previous section:
让我们看看上一节中我们的简单图的邻接列表是什么样子的。
This representation is comparatively difficult to create and less efficient to query. However, it offers better space efficiency.
这种表示方法相对难以创建,而且查询效率较低。然而,它提供了更好的空间效率。
We’ll use the adjacency list to represent the graph in this tutorial.
在本教程中,我们将使用邻接列表来表示图。
4. Graphs in Java
4.Java中的图表
Java doesn’t have a default implementation of the graph data structure.
Java没有一个默认的图数据结构的实现。
However, we can implement the graph using Java Collections.
然而,我们可以用Java集合来实现图。
Let’s begin by defining a vertex:
让我们首先定义一个顶点。
class Vertex {
String label;
Vertex(String label) {
this.label = label;
}
// equals and hashCode
}The above definition of vertex just features a label, but this can represent any possible entity such as Person or City.
上述顶点的定义只是以一个标签为特征,但这可以代表任何可能的实体,如Person或City。
Also, note that we have to override the equals() and hashCode() methods as these are necessary to work with Java Collections.
此外,请注意我们必须覆盖equals()和hashCode()方法,因为这些方法对于使用Java集合是必要的。
As we discussed earlier, a graph is nothing but a collection of vertices and edges that can be represented as either an adjacency matrix or an adjacency list.
正如我们前面所讨论的,图只不过是一个顶点和边的集合,可以表示为邻接矩阵或邻接列表。
Let’s see how we can define this using an adjacency list here:
让我们看看我们如何在这里用邻接列表来定义这个。
class Graph {
private Map<Vertex, List<Vertex>> adjVertices;
// standard constructor, getters, setters
}As we can see, the class Graph is using Map from Java Collections to define the adjacency list.
我们可以看到,Graph类使用Java集合中的Map来定义邻接列表。
There are several operations possible on a graph data structure, such as creating, updating or searching through the graph.
在图数据结构上有几种可能的操作,如创建、更新或搜索通过图。
We’ll go through some of the more common operations and see how we can implement them in Java.
我们将通过一些比较常见的操作,看看我们如何在Java中实现它们。
5. Graph Mutation Operations
5.图谱突变操作
To start with, we’ll define some methods to mutate the graph data structure.
首先,我们将定义一些方法来突变图的数据结构。
Let’s define methods to add and remove vertices:
我们来定义添加和删除顶点的方法。
void addVertex(String label) {
adjVertices.putIfAbsent(new Vertex(label), new ArrayList<>());
}
void removeVertex(String label) {
Vertex v = new Vertex(label);
adjVertices.values().stream().forEach(e -> e.remove(v));
adjVertices.remove(new Vertex(label));
}These methods simply add and remove elements from the vertices Set.
这些方法只是从顶点集中添加和删除元素。
Now let’s also define a method to add an edge:
现在让我们也定义一个方法来添加一个边缘。
void addEdge(String label1, String label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
adjVertices.get(v1).add(v2);
adjVertices.get(v2).add(v1);
}This method creates a new Edge and updates the adjacent vertices Map.
该方法创建一个新的Edge并更新相邻的顶点Map。
In a similar way, we’ll define the removeEdge() method:
以类似的方式,我们将定义removeEdge()方法。
void removeEdge(String label1, String label2) {
Vertex v1 = new Vertex(label1);
Vertex v2 = new Vertex(label2);
List<Vertex> eV1 = adjVertices.get(v1);
List<Vertex> eV2 = adjVertices.get(v2);
if (eV1 != null)
eV1.remove(v2);
if (eV2 != null)
eV2.remove(v1);
}Next, let’s see how we can create the simple graph we drew earlier using the methods we’ve defined so far:
接下来,让我们看看如何使用我们到目前为止定义的方法来创建我们之前画的简单图形。
Graph createGraph() {
Graph graph = new Graph();
graph.addVertex("Bob");
graph.addVertex("Alice");
graph.addVertex("Mark");
graph.addVertex("Rob");
graph.addVertex("Maria");
graph.addEdge("Bob", "Alice");
graph.addEdge("Bob", "Rob");
graph.addEdge("Alice", "Mark");
graph.addEdge("Rob", "Mark");
graph.addEdge("Alice", "Maria");
graph.addEdge("Rob", "Maria");
return graph;
}Finally, we’ll define a method to get the adjacent vertices of a particular vertex:
最后,我们将定义一个方法来获取某个特定顶点的相邻顶点。
List<Vertex> getAdjVertices(String label) {
return adjVertices.get(new Vertex(label));
}6. Traversing a Graph
6.遍历图形
Now that we have the graph data structure and functions to create and update it defined, we can define some additional functions for traversing the graph.
现在我们已经定义了图的数据结构以及创建和更新它的函数,我们可以定义一些额外的函数来遍历图。
We need to traverse a graph to perform any meaningful action, such as search within the graph.
我们需要遍历一个图来执行任何有意义的行动,比如在图中搜索。
There are two possible ways to traverse a graph: depth-first traversal and breadth-first traversal.
有两种可能的方法来遍历一个图:深度优先遍历和广度优先遍历。
6.1. Depth-First Traversal
6.1.深度优先遍历
A depth-first traversal starts at an arbitrary root vertex and explores vertices as deep as possible along each branch before exploring vertices at the same level.
一个深度优先遍历从一个任意的根顶点开始,沿每个分支尽可能深入地探索顶点,然后再探索同一层次的顶点。
Let’s define a method to perform the depth-first traversal:
让我们定义一个方法来执行深度优先的遍历。
Set<String> depthFirstTraversal(Graph graph, String root) {
Set<String> visited = new LinkedHashSet<String>();
Stack<String> stack = new Stack<String>();
stack.push(root);
while (!stack.isEmpty()) {
String vertex = stack.pop();
if (!visited.contains(vertex)) {
visited.add(vertex);
for (Vertex v : graph.getAdjVertices(vertex)) {
stack.push(v.label);
}
}
}
return visited;
}Here, we’re using a Stack to store the vertices that need to be traversed.
这里,我们使用一个Stack来存储需要遍历的顶点。
Let’s run this on the graph we created in the previous subsection:
让我们在上一小节中创建的图形上运行这个程序。
assertEquals("[Bob, Rob, Maria, Alice, Mark]", depthFirstTraversal(graph, "Bob").toString());Please note that we’re using vertex “Bob” as our root for traversal here, but this can be any other vertex.
请注意,我们在这里使用顶点 “Bob “作为我们的遍历根,但这可以是任何其他顶点。
6.2. Breadth-First Traversal
6.2.广度优先遍历
Comparatively, a breadth-first traversal starts at an arbitrary root vertex and explores all neighboring vertices at the same level before going deeper in the graph.
相对而言,广度优先遍历从一个任意的根顶点开始,在深入到图中之前,先探索同一层次的所有相邻顶点。
Now let’s define a method to perform the breadth-first traversal:
现在让我们定义一个方法来执行广度优先的遍历。
Set<String> breadthFirstTraversal(Graph graph, String root) {
Set<String> visited = new LinkedHashSet<String>();
Queue<String> queue = new LinkedList<String>();
queue.add(root);
visited.add(root);
while (!queue.isEmpty()) {
String vertex = queue.poll();
for (Vertex v : graph.getAdjVertices(vertex)) {
if (!visited.contains(v.label)) {
visited.add(v.label);
queue.add(v.label);
}
}
}
return visited;
}Note that a breadth-first traversal makes use of Queue to store the vertices that need to be traversed.
请注意,广度优先遍历使用Queue来存储需要遍历的顶点。
Let’s again run this traversal on the same graph:
让我们再次在同一个图上运行这个遍历。
assertEquals(
"[Bob, Alice, Rob, Mark, Maria]", breadthFirstTraversal(graph, "Bob").toString());Again, the root vertex, which is “Bob” here, can just as well be any other vertex.
同样,根顶点,也就是这里的 “鲍勃”,也可以是任何其他顶点。
7. Java Libraries for Graphs
7.图形的Java库
It’s not necessary to always implement the graph from scratch in Java. There are several open source and mature libraries available that offer graph implementations.
没有必要总是用Java从头开始实现图。有几个开源和成熟的库可以提供图的实现。
In the next few subsections, we’ll go through some of these libraries.
在接下来的几个小节中,我们将对这些库中的一些进行介绍。
7.1. JGraphT
7.1. JGraphT
JGraphT is one of the most popular libraries in Java for the graph data structure. It allows the creation of a simple graph, directed graph and weighted graph, among others.
JGraphT是Java中最流行的图数据结构库之一。它允许创建简单图、有向图和加权图等。
Additionally, it offers many possible algorithms on the graph data structure. One of our previous tutorials covers JGraphT in much more detail.
此外,它还提供了许多关于图数据结构的可能算法。我们以前的一个教程更详细地介绍了JGraphT。
7.2. Google Guava
7.2.Google Guava
Google Guava is a set of Java libraries that offer a range of functions including graph data structure and its algorithms.
Google Guava是一组Java库,提供一系列功能,包括图数据结构及其算法。
It supports creating simple Graph, ValueGraph and Network. These can be defined as Mutable or Immutable.
它支持创建简单的Graph、ValueGraph和Network。这些可以被定义为Mutable或Immutable。
7.3. Apache Commons
7.3.阿帕奇共享空间
Apache Commons is an Apache project that offers reusable Java components. This includes Commons Graph that offers a toolkit to create and manage graph data structure. This also provides common graph algorithms to operate on the data structure.
Apache Commons是一个Apache项目,提供可重用的Java组件。其中包括Commons Graph,它提供了一个用于创建和管理图形数据结构的工具包。这也提供了常见的图算法,以便对数据结构进行操作。
7.4. Sourceforge JUNG
7.4.Sourceforge JUNG
Java Universal Network/Graph (JUNG) is a Java framework that provides extensible language for modeling, analysis and visualization of any data that can be represented as a graph.
Java通用网络/图形(JUNG)是一个Java框架,为任何可以表示为图形的数据的建模、分析和可视化提供可扩展的语言。
JUNG supports many algorithms that include routines such as clustering, decomposition and optimization.
JUNG支持许多算法,包括聚类、分解和优化等程序。
These libraries provide a number of implementations based on the graph data structure. There are also more powerful frameworks based on graphs, such as Apache Giraph, currently used at Facebook to analyze the graphs formed by their users, and Apache TinkerPop, commonly used on top of graph databases.
这些库提供了一些基于图数据结构的实现。还有一些基于图的更强大的框架,例如Apache Giraph,目前在Facebook用于分析其用户形成的图,以及Apache TinkerPop,通常用于图数据库之上。
8. Conclusion
8.结论
In this article, we discussed the graph as a data structure along with its representations. We defined a very simple graph in Java using Java Collections and also defined common traversals for the graph.
在这篇文章中,我们讨论了作为数据结构的图及其表示方法。我们在Java中使用Java集合定义了一个非常简单的图,还为图定义了常见的遍历方法。
We also talked briefly about various libraries available in Java outside the Java platform that provide graph implementations.
我们还简单地谈到了Java平台之外的各种提供图实现的库。
As always, the code for the examples is available over on GitHub.
像往常一样,这些例子的代码可以在GitHub上找到over。