1. Introduction
1.绪论
In this tutorial, we’ll discuss the gravity sort algorithm and its single-threaded implementation in Java.
在本教程中,我们将讨论重力排序算法及其在Java中的单线程实现。
2. The Algorithm
2.算法
Gravity sort is a natural sorting algorithm inspired by natural events – in this case, the force of gravity. Also known as Bead Sort, this algorithm simulates the force of gravity to sort a list of positive integers.
重力排序是一种自然的排序算法,其灵感来自于自然事件–在这种情况下,就是重力。也被称为珠子排序,这种算法模拟引力对正整数列表进行排序。
The idea of the algorithm is to represent positive integers using beads in vertical rods and horizontal levels – similar to an abacus, except that every level represents a single number of the input list. The next step is to drop the beads to their lowest possible position, which results in the abacus having an ascending order of the numbers:
该算法的想法是用垂直杆和水平层的珠子来表示正整数–类似于算盘,只不过每一层都代表输入列表中的一个数字。下一步是将珠子降到它们可能的最低位置,这导致算盘上的数字呈升序排列。
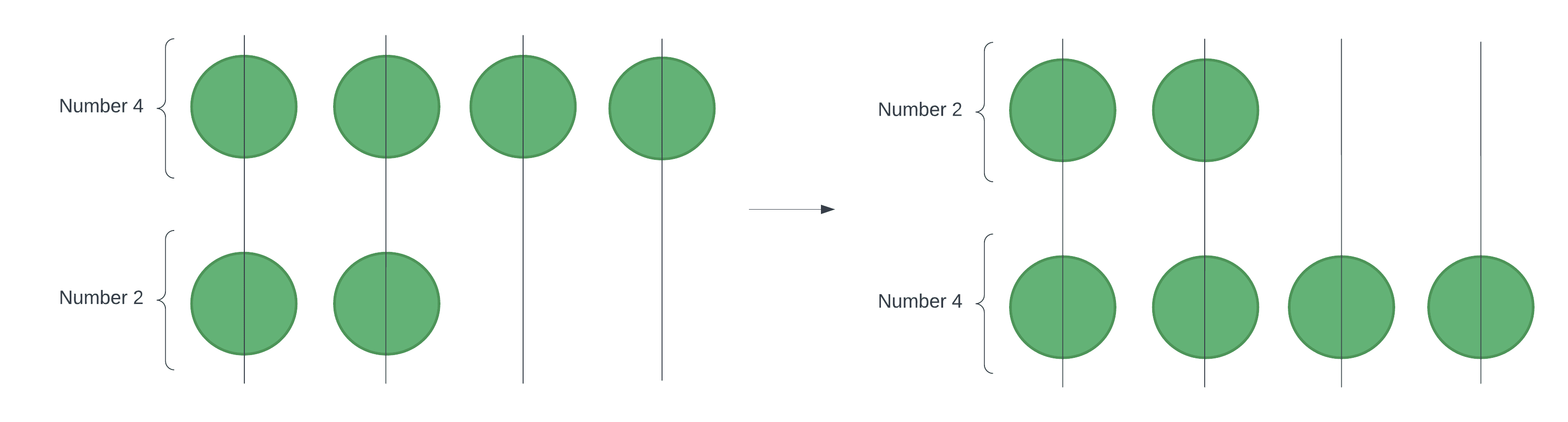
For example, here’s the process of sorting an input list of [4, 2]:
例如,下面是对一个输入列表[4, 2]进行排序的过程。
We apply the force of gravity to the abacus. Subsequently, all beads will be at their lowest possible position after falling. The resulting state of the abacus is now an ascending order of positive integers from top to bottom.
我们对算盘施加重力。随后,所有的珠子在落下后都会处于可能的最低位置。现在,算盘的结果状态是正整数从上到下的升序。
In reality, gravity drops all the beads at the same time. However, in software, we must simulate the beads falling in different iterations. Next, we’ll look at how we can represent the abacus as a two-dimensional array, and how we can simulate the falling beads to sort the numbers of the list.
在现实中,重力使所有的珠子在同一时间掉落。然而,在软件中,我们必须模拟珠子以不同的迭代方式落下。接下来,我们将看看如何将算盘表示为一个二维数组,以及如何模拟珠子的下落来对列表的数字进行排序。
3. Implementation
3.实施
To implement gravity sort in software, we’ll follow the pseudocode in this article to write the code in Java.
为了在软件中实现重力排序,我们将按照本文中的伪代码,在Java中编写代码。
First, we need to transform the input list into an abacus. We’ll use a two-dimensional array to represent the rods (columns) and levels (rows) as the dimensions of the matrix. Additionally, we’ll use true or false to indicate a bead or an empty cell, respectively.
首先,我们需要将输入列表转化为一个算盘。我们将使用一个二维数组来表示棒(列)和水平(行)作为矩阵的尺寸。此外,我们将使用true或false来分别表示一个珠子或一个空单元。
Before setting up our abacus, let’s find the dimensions of the matrix. The number of columns m equals the largest element in the list. Therefore, let’s create a method to find this number:
在设置我们的算盘之前,让我们先找出矩阵的尺寸。列数m等于列表中最大的元素。因此,让我们创建一个方法来寻找这个数字。
static int findMax(int[] A) {
int max = A[0];
for (int i = 1; i < A.length; i++) {
if (A[i] > max) {
max = A[i];
}
}
return max;
}Now, we’re able to assign the largest number to m:
现在,我们能够把最大的数字分配给m。
int[] A = {1, 3, 4, 2};
int m = findMax(A);With m, we are now able to create a representation of the abacus. We’ll use the setupAbacus() method to do this:
通过m,我们现在能够创建一个算盘的表示。我们将使用setupAbacus()方法来完成这个任务。
static boolean[][] setupAbacus(int[] A, int m) {
boolean[][] abacus = new boolean[A.length][m];
for (int i = 0; i < abacus.length; i++) {
int number = A[i];
for (int j = 0; j < abacus[0].length && j < number; j++) {
abacus[A.length - 1 - i][j] = true;
}
}
return abacus;
}The setupAbacus() method returns the initial state of the abacus. The method goes through every cell in the matrix, assigning a bead or an empty cell.
setupAbacus()方法返回算盘的初始状态。该方法遍历矩阵中的每一个单元格,分配一个珠子或一个空单元格。
At every level in the matrix, we’ll use the ith number in list A to determine the number of beads in a row. Moreover, we iterate through every column j, and if number is greater than the jth column index, we mark this cell true to indicate a bead. Otherwise, the loop terminates early, leaving the rest of the cells empty or false in the ith row.
在矩阵的每一级,我们将使用列表i中的第number来确定一行中的珠子数量。此外,我们遍历每一列j,如果number大于j第1列索引,我们将此单元格标记为true以表示有珠子。否则,循环就会提前终止,让其余的单元格为空或false在i第行。
Let’s create the abacus:
让我们来创造算盘。
boolean[][] abacus = setupAbacus(A, m);We’re now ready to let gravity sort the beads by dropping them to their lowest possible positions:
我们现在准备让重力对珠子进行分类,把它们丢到它们可能的最低位置。
static void dropBeads(boolean[][] abacus, int[] A, int m) {
for (int i = 1; i < A.length; i++) {
for (int j = m - 1; j >= 0; j--) {
if (abacus[i][j] == true) {
int x = i;
while (x > 0 && abacus[x - 1][j] == false) {
boolean temp = abacus[x - 1][j];
abacus[x - 1][j] = abacus[x][j];
abacus[x][j] = temp;
x--;
}
}
}
}
}Initially, the dropBeads() method loops through every cell in the matrix. Starting at 1, i is the row to start with, since there won’t be any beads to drop from the bottom-most level 0. With respect to the columns, we start with j = m – 1 to start dropping the beads from right to left.
最初,dropBeads()方法会循环查看矩阵中的每个单元。从1开始,i是要开始的行,因为不会有任何珠子从最底层的0级开始掉落。关于列,我们从j = m – 1 开始,从右到左开始投掷珠子。
In every iteration, we check whether the current cell, abacus[i][j], contains a bead. If so, we use a variable x to store the current level of the falling bead. We drop the bead by decreasing x as long as it’s not the bottom-most level, and the cell below is an empty space.
在每个迭代中,我们检查当前单元格abacus[i][j]是否包含一个珠子。如果是的话,我们用一个变量x来存储当前下降的珠子的水平。 我们通过减少x来下降珠子,只要它不是最底层,并且下面的单元格是一个空的空间。
Lastly, we need to transform the final state of the abacus into a sorted array. The toSortedList() method takes in the abacus as a parameter, along with the original input list, and modifies the array accordingly:
最后,我们需要将算盘的最终状态转化为一个排序的数组。toSortedList()方法将算盘和原始输入列表作为一个参数,并对数组进行相应的修改。
static void toSortedList(boolean[][] abacus, int[] A) {
int index = 0;
for (int i = abacus.length - 1; i >=0; i--) {
int beads = 0;
for (int j = 0; j < abacus[0].length && abacus[i][j] == true; j++) {
beads++;
}
A[index++] = beads;
}
}We can recall that the number of beads in every row represents a single number in the list. For that reason, the method iterates through every level in the abacus, counts the beads, and assigns the value to the list. The method sets the values in ascending order starting at the highest row value. However, starting with i = 0, it places the numbers in descending order.
我们可以回顾一下,每一行的珠子数量代表了列表中的一个数字。出于这个原因,该方法迭代了算盘中的每一层,对珠子进行计数,并将数值分配给列表。该方法按升序设置数值从最高行数值开始。然而,从i = 0开始,它将数字按降序排列。
Let’s put all pieces of the algorithm together into a single gravitySort() method:
让我们把算法的所有部分整合到一个单一的gravitySort()方法中:。
static void gravitySort(int[] A) {
int m = findMax(A);
boolean[][] abacus = setupAbacus(A, m);
dropBeads(abacus, A, m);
transformToList(abacus, A);
}We can confirm the algorithm works by creating a unit test:
我们可以通过创建一个单元测试来确认该算法的工作。
@Test
public void givenIntegerArray_whenSortedWithGravitySort_thenGetSortedArray() {
int[] actual = {9, 9, 100, 3, 57, 12, 3, 78, 0, 2, 2, 40, 21, 9};
int[] expected = {0, 2, 2, 3, 3, 9, 9, 9, 12, 21, 40, 57, 78, 100};
GravitySort.sort(actual);
Assert.assertArrayEquals(expected, actual);
}4. Complexity Analysis
4.复杂度分析
We saw that the gravity sort algorithm entails a lot of processing. Therefore, let’s break it down into time and space complexity.
我们看到,重力排序算法需要大量的处理。因此,让我们把它分解成时间和空间的复杂性。
4.1. Time Complexity
4.1.时间复杂度
The implementation of the gravity sort algorithm starts with finding the maximum number m in the input list. This process is an O(n) runtime operation as we pass through the array once. Once we obtain m, we set up the initial state of the abacus. Because the abacus is really a matrix, visiting every cell in every row and column results in an O(m * n) operation where n is the number of rows.
重力排序算法的实现从寻找输入列表中的最大数字m开始。这个过程是一个O(n)运行时的操作,因为我们在数组中传递了一次。一旦我们得到m,我们就设置了算盘的初始状态。因为算盘实际上是一个矩阵,访问每一行和每一列的每一个单元格都会产生O(m * n)操作,其中n是行的数量。
Once our setup is ready, we must drop the beads to their lowest possible position in the matrix, as though gravity is affecting our abacus. Again, we’re visiting every cell in the matrix along with an inner loop that drops the beads at most n levels in every column. This process has an O(n * n * m) runtime.
一旦我们的设置准备好了,我们必须把珠子丢到矩阵中的最低位置,就像重力影响我们的算盘一样。同样,我们要访问矩阵中的每一个单元格,同时还有一个内循环,把珠子丢到每一列的最多n级。这个过程有一个O(n * n * m)运行时间。
Further, we must perform O(n) additional steps to recreate our list based on the sorted representation in the abacus.
此外,我们必须执行O(n)额外步骤,根据算盘中的排序表示重新创建我们的列表。
Overall, gravity sort is an O(n * n * m) algorithm, considering its effort to simulate the beads falling.
总的来说,考虑到其模拟珠子下落的努力,重力排序是一种O(n * n * m)算法。
4.2. Space Complexity
4.2.空间复杂度
The space complexity for gravity sort is proportional to the size of the input list and its largest number. For example, a list with n number of elements and a maximum number m requires a matrix representation of n x m dimensions. Consequently, the space complexity is O(n * m) to allocate extra space in memory for the matrix.
引力排序的空间复杂度与输入列表的大小及其最大数成正比。例如,一个有n个元素和最大数m的列表需要一个n x m维的矩阵表示。因此,空间复杂度是O(n * m),要在内存中为矩阵分配额外空间。
Nonetheless, we try to minimize the space complexity by representing beads and empty cells with single bits or numbers. Namely, 1 or true indicates a bead, and similarly, a 0 or false value is an empty cell.
尽管如此,我们还是试图通过用单个比特或数字来表示珠子和空单元来尽量减少空间的复杂性。也就是说,1或true表示一个珠子,同样,0或false值是一个空单元。
5. Conclusion
5.总结
In this article, we learned how to implement a single-threaded approach for the gravity sort algorithm. Also called bead sort, this algorithm is inspired by the force of gravity naturally sorting positive integers that we represent as beads in an abacus. Yet, in software, we use a two-dimensional matrix and single-bit values to reproduce this environment.
在这篇文章中,我们学习了如何实现重力排序算法的单线程方法。这个算法也被称为珠子排序,它的灵感来自于重力自然排序的正整数,我们在算盘上表示为珠子。然而,在软件中,我们使用一个二维矩阵和单比特值来重现这种环境。
Although the single-threaded implementation has a costly time and space complexity, this algorithm performs well in hardware and multi-threaded applications. Nonetheless, the gravity sort algorithm exemplifies how natural events can inspire solutions to software implementations.
虽然单线程的实现具有昂贵的时间和空间复杂度,但这种算法在硬件和多线程的应用中表现良好。尽管如此,重力排序算法还是体现了自然事件是如何激发软件实现的解决方案的。
As always, the code for the implementation of this algorithm can be found over on GitHub.
一如既往,该算法的实现代码可以在GitHub上找到over。